第七届“华罗庚金杯”少年数学邀请赛
初赛试题
1、把1999分成两个质数的和，有多少种方法。
2、澳门人口43万，90%居住在半岛上，半岛面积7平方千米，求半岛上平均每平方千米有多少万人?(取两位小数)
3、某人去年买一种股票,当年下跌了20%,今年应上涨百分之几，才能保持原值。
4.某个月里有三个星期日的日期为偶数,请推算出这个月的15日是星期几?
5.火树银花楼七层,层层红灯倍加增,共有红灯三八一,试问四层几红灯?
6.左下图是由9个等边三角形拼成的图形,已知中间最小的等边三角形的边长是1,求这个六边形的周长是多少?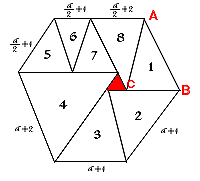 
7.一个正六边形的苗圃,用平行于苗圃边缘的直线,把它分成许多相等的正三角形,在三角形的顶点上都栽种上树苗,已知苗圃的最外面一圈栽有90棵，请问苗圃中共栽树苗多少棵?
8.甲、乙、丙三所小学人数的总和为1999,已知甲校学生人数的两倍,乙校学生人数减3,丙校学生人数加4都是相等的。问甲、乙、丙各校学生人数是多少?
9.小明爷爷的年龄是一个两位数,将此两位数的数字交换得到的数就是小明爸爸的年龄,他俩年龄之差是小明年龄的4倍,求小明的年龄?
10.用10块长7厘米,宽5厘米,高3厘米的长方体积木拼成一个长方体,问这个长方体的表面积最小是多少?
11.时钟的时针和分针在6点钟恰好反向成一条直线,问下一次反向成一条直线是什么时间?(准确到秒)
第七届“华罗庚金杯”少年数学邀请赛 初赛试题解答
1、 答案：1种。
解：在所有的质数中，只有2是偶数，其它都是奇数。1999是奇数，不可能分成两个奇质数的和，一定是一奇一偶的情形。(1999＝2＋1997)此题有唯一的解。
注：本题的实质是考察在质数中只有一个是偶数，另外奇数分成两个整数的和只能是一个是奇数，另一个是偶数，懂得了这个道理，问题便迎刃而解。
2、 答案：5.53万人。
解：先求半岛上共有多少万人： 43×90%＝38.7(万人)
再求平均每平方千米的人数是多少? 38.7÷7≈5.53(万人)
综合算式:43×90%÷7≈5.53(万人)
注：本题是一道简单的应用题，只是要求我们计算时要准确、迅速。
3、 答案：25%
解：设某人去年买股票A元,下跌后剩下A×(1－20%)＝4/5 A(元)
如果今年上涨X%才能保值,那么(4/5)A(1＋X%)=A
1+X%=1(1/4)
X%=25%
注:1(1/4)表示一又四分之一。这道题如果我们灵活地“设计”数据,假设某人去年买股票100元,下跌20%后,剩下80元,再求100比80多百分之几?(100-80)/80＝25%,25%就是今年应上涨的百分率。
4. 答案:星期六。
解:每个月里,日期为偶数的编号从小到大依次排列为2,4,6,……28或(30)。 我们不妨设这个月的2号是星期日,那么,本月的16号,30号都是星期日,这是符合要求的。因此,这个月的15号是星期六。
注:一个月最多只有31天,事实上,如果这个月的4号是星期日,那么第三个星期日就是4+28=32(号),这与实际不相符,懂得了这个道理,对于这道题就能准确、迅速地作出判断。
5. 答案:第四层有红灯24盏。
解:这首诗告诉我们,七层楼上红灯数目呈倍数递增,为了求出第四层上红灯的数目,我们可先分解381。
381=3×127 而127=2＾7-1=1+2+4+8+16+32+64
各层上的红灯数从上到下依次是：第七层:3×1
第六层:3×2
第五层:3×4
第四层:3×8
……
第一层:3×64
因此,第四层上的红灯数为3×8=24(盏)。
注: 2＾7表示二的七次方。分解质因数可找到解答本题的突破口。
6. 答案:30。
解:设下图中等边三角形ABC的边长为a,按顺时针方向,六边形所在的正三角形2,3,4,5,6,8的边长依次是:2号:a+1,3号:a+1,4号:a+2,5号:(a/2)+1,6号:(a/2)+1,8号:(a/2)+2。
由于编号8的正三角形的边长是(a/2)+2,它与所设三角形ABC的边长a相等, 这样可求得a的值:(a/2)+2=a,解得a=4。这样,六边形的周长为:
a+(a+1)+(a+1)+(a+2)+[(a/2)+1]+[(a/2)+1]+[(a/2)+2]
=5(1/2)a+8=5(1/2)×4+8=30
注:5(1/2)表示五又二分之一。这道题通过“形”的组合,隐藏并反映“数”的等量关系,找出等量关系后,使题目容易求解。
7. 答案:721棵。
解:由正六边形苗圃的最外面一圈栽有90棵树苗,可求得每边(外围)上的树苗为:
90÷6=15(棵)
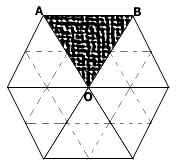
我们将正六边形分成六个相同的小正三角形:
(如右图三角形ABC),每个正三形 里种有树苗:
15+14+13+……+2+1=120(棵)
六个三角形共种有树:120×6=720(棵)
但中心点还种有一棵树,因此苗圃中共种有树苗720+1=721(棵)。
注:同学们知道等差数列求和的计算方法,这道题相当于告诉了等差数列的末项,需灵活地求出它的首项和项数,另外不可忽视正六边形的中点,对于这道题,还有另外的解法。如:90+(90-6×1)=(90-6×2)+(90-6×3)+……+(90-6×14)+1=721(棵)。
8. 答案:甲400,乙803,丙796。
解:设相等时的人数为A,那么甲、乙、丙各校的人数分别为:
甲(1/2) A人,乙(A+3)人,丙(A－4)人。
根据题意列方程得:
（1/2)A+(A+3)+(A-4)=1999
解得A=800
甲校人数800×(1/2)=400(人)
乙校人数800+3=803(人)
丙校人数800-4=796(人)
注:依甲、乙、丙三所小学相等时的人数,通过逆推,用分别含有一个相同字母的式子表示各校的人数列出方程,是解答本题的技巧。
9. 答案:9岁。
解:设小明爷爷的年龄为两位数
,则他爸爸的年龄为
,那么有4能整除(-)
也就是4能整除[9(A-B)]
当A-B=4时,小明年龄为9×4÷4=9(岁)
当A-B=8时,小明9×8÷4=18(岁)
爷爷91岁,爸爸19岁,不符合要求。
因此,小明的年龄是9岁。
注:解答本题的关键是求一个两位数,交换数位顺序后所得到的新两位数与原数的差能被4整除。
10. 答案:650平方厘米。
解:把这10块积木拼成如下情形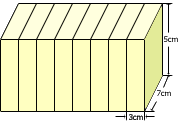
,其表面积不是最小的。
要使长方体的表面积尽量的小,必须使拼成的长方体重合的面积尽量的大。如果能够 拼成正方体或接近正方体时,其表面积较小。拼完后,长方体的体积为:3×5×7×10 =3×5×7×(2×5) 这里我们注意长方体的长,宽,高尽量的靠近。2×3×5×5×7=7×(2×5)×(3×5)=7×10×15
如图拼法: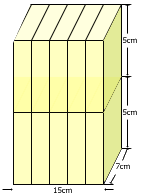
其表面积为:(7×10+10×15+7×15)×2=650(平方厘米)
注:解答本题的关键是懂得一个道理：当体积一定时,正方体的表面积比长方体的表面积小。
11. 答案:7点5分27秒。
解:当下一次时针与分针反向成一条直线时,分针比时针多行一圈。
我们知道,一圈有360°,不妨设计一种追及路程为度的方法:
时针每分行360°×(1/12)
×(1/60)=0.5°
分针每分行360°×(1/60)=6°
追及“路程”为360°
追及时间:360÷(6-0.5)=65(5/11)(分)
65(5/11)=1小时5分27秒,下一次时针与分针恰好反向成一条直线的时间是7点5分27秒。
注：65(5/11)表示六十五又十一分之五。