数学七年级上册期末综合测试卷(三)
一、填空题(每题3分,共30分)
1.单项式-![]() a2bc的系数是__________;次数是_________.
a2bc的系数是__________;次数是_________.
2.我国自行研制的“神舟五号”载人飞船于二00三年十月十五日成功发射,并环绕地球飞行约590520千米,请将这一数字用科学记数法表示为_______千米(要求保留一位有效数字).
3.如图,要给这个长、宽、高分别为x、y、z的 箱子打包,其打包方式如右图所示,则打包带的长至少要______ ___ (单位:mm)(用含x、y、z的代数式表示) .
箱子打包,其打包方式如右图所示,则打包带的长至少要______ ___ (单位:mm)(用含x、y、z的代数式表示) .
4.若![]() 与|b+1的值互为相反数,则a+b=
.
与|b+1的值互为相反数,则a+b=
.
5.若a、b都是无理数,且![]() ,则
,则![]() 的值可以是
的值可以是
_________________.(填上一组满足条件的值即可)
6. ∠1与∠2互余,∠2与∠3互补,∠1=63°,那么∠3= .
7.已知a、b互为相反数,c、d互为倒数,x的绝对值为5,则x2+(a+b)2002+(-cd)2003的值为_________________.
8.某城市自来水收费实行阶梯水价,收费标准如下表所示,用户5月份交水费45元,则所用水为 度.
| 月用水量 | 不超过12度的部分 | 超过12度不超过18度的部分 | 超过18度的部分 |
| 收费标准(元/度) | 2.00 | 2.50 | 3.00 |
9.用计数器探索:按一定规律排列的一组数:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,如果从中选出若干个数,使它们的和大于0.5,那么至少要选
个数.
,如果从中选出若干个数,使它们的和大于0.5,那么至少要选
个数.
10.观察下列各式:![]()
……请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来是___ ________ _______.
二、选择题(每题2分,共20分)
11.计算2a-2(a+1)的结果是 ( )
A.-2 B.2 C.-1 D.1
12.如图,![]() 和
和![]() 都是直角,如果∠AOD=150°,那么∠COB=( )
都是直角,如果∠AOD=150°,那么∠COB=( )
A.
![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
13.实数0、![]() 、-
、-![]() 、π中,无理数有 ( )
、π中,无理数有 ( )
A.1个 B.2个 C.3个 D.4个
14.若![]() ,则实数a在数轴上的对应点一定在( )
,则实数a在数轴上的对应点一定在( )
A.原点左侧 B.原点右侧 C.原点或原点左侧 D.原点或原点右侧
15.下列说法错误的是 ( )
A. ![]() 的平方根是
的平方根是![]() B.绝对值等于它的相反数的数一定是负数
B.绝对值等于它的相反数的数一定是负数
C.单项式![]() 与
与![]() 是同类项 D.近似数
是同类项 D.近似数![]() 有三个有效数字
有三个有效数字
16.下列说法正确的是 ( )
A.两点之间的距离是两点间的线段;
B.同一平面内,过一点有且只有一条直线与已知直线平行;
C.同一平面内,过一点有且只有一条直线与已知直线垂直;
D.与同一条直线垂直的两条直线也垂直.
17.某种细菌在培养过程中,每半小时分裂1次,每次一分为二。若这种细菌由1个分裂到16个,那么这个过程要经过( )
A.1.5小时 B.2小时 C.3小时 D.4小时
18.如图.把一个正方形三次对折后沿虚线剪下.则所得图形是 ( )

19.按下列图示的程序计算,若开始输入的值为x=3,则最后输出的结果是( )

A.6 B.21 C.156 D.231
20.某超市推出如下优惠方案:(1)一次性购物不超过100元不享受优惠.(2)一次性购物超过100元,但不超过300元一律9折,(3)一次性购物超过300元一律8折.王波两次购物分别付款80元、252元.如果他一次性购买与上两次相同的商品,则应付款 ( )
A.228元 B.332元 C.228或316元 D.332或363元
三、解答题(21~25题每题6分,26~27每题10分,共50分)
21.已知a=-2,b=-1,c=3,求代数式5abc-2a2b+[3abc-(4ab2-a2b)]的值。
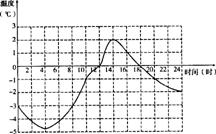 22.下面的图象记录了某地一月份某天的温度随时间变化的情况,请你仔细观察图象回答下面的问题:
22.下面的图象记录了某地一月份某天的温度随时间变化的情况,请你仔细观察图象回答下面的问题:
(1)20时的温度是 ℃,温度是O℃的时刻是 时,最暖和的时刻是 时,温度在-3℃以下的持续时间为 小时.
(2)你从图象中还能获取哪些信息(写出1~2条即可)?
.
23.下表是对育才中学七年级(2)班的同学就“父母回家后,你会主动给他们倒一杯水吗?”情况调查结果,请你按照要求用扇形统计图表示该调查结果
(1)计算各类人数所占百分比及各个扇形圆心角的度数,并填入下表:
(2)制作扇形统计图,标上相应的类及百分比,并写上统计图的名称
| 人数 | |
| 主动倒水(A) | 27 |
| 偶尔倒水(B) | 18 |
| 不倒水(C) | 15 |
| 主动倒水 | 偶尔倒水 | 不倒水 | |
| 百分比 | |||
| 圆心角度数 |
24.某市的出租车因车型不同,收费标准也不同:A型车的起步价10元,3千米后每千米价为1.2元;B型车的起步价8元,3千米后每千米价为1.4元。
(1)如果你要乘坐出租车到20千米处的地方,从节省费用的角度,你应该乘坐哪种型号的出租车?
(2)请你计算乘坐A型与B型出租车x(x>3)千米的价差是多少元?
25.先阅读下面例题的解题过程,再解答后面的题目.
例:已知代数式![]() ,求
,求![]() 的值.
的值.
解:由![]() 得
得![]() , 即
, 即 ![]()
因此![]() , 所以
, 所以![]() =8
=8
题目:已知代数式![]() =-2,求
=-2,求![]() 的值.
的值.
26.如图是某月的日历表:
(1)表中方框里的5个数的和与方框中间的数有何关系?
(2)这种关系对任意这种的方框都适用吗?若中间这个数为a,则这5个数之和请用a的代数式表示;
 (3)方框中的五个数之和能等于2005吗?若能,请写出这五个数;若不能,请说明理由.
(3)方框中的五个数之和能等于2005吗?若能,请写出这五个数;若不能,请说明理由.
27.某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售,每吨利润7000元。当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行。受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕。为此,公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案,说说理由.