2004—2005学年度第一学期期末考试初一数学试卷
一、选择题(本大题共10小题,每小题2分,共20分。每小题只有一个选项是正确的,把正确选项前的字母填在下表中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1.![]() 的相反数是 (A)3
(B)―3
(C)
的相反数是 (A)3
(B)―3
(C) ![]() (D)―
(D)―![]()
2.方程![]() x=3的解是 (A)x=6 (B)x=―6
(C)x=
x=3的解是 (A)x=6 (B)x=―6
(C)x=![]() (D)x=
(D)x=![]()
3.在―(―6),―(―6)2,―6,―62这四个数中,负数的个数为
(A)1个 (B)2个 (C)3个 (D)4个
4.当a=―5,b=―3时,代数式2b2―5a的值等于
(A)18 (B)―18 (C)43 (D)―43
5.如果―![]() x2a―1y6与―2xy6是同类项,则代数式(a—2)2004·(2a—1)2005的值是
x2a―1y6与―2xy6是同类项,则代数式(a—2)2004·(2a—1)2005的值是
(A)0 (B)1 (C)―1 (D)1或―1
 6.若x=3,y=2,xy<0,则x+y的值等于
6.若x=3,y=2,xy<0,则x+y的值等于
(A)5或―5 (B)1或―1 (C)5或1 (D)―5或1
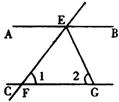
7.如图,AB∥CD,直线EF分别交AB、CD于点E、F,
BG平分∠BEF,∠l=50°,则∠2为
(A)50° (B)60° (C)65° (D)70°
8.下面事倩中必然事情是
(A)打开电视机,它正好播广告 (B)异号两数相加,和为零
(C)黑暗中我从一大串钥匙中选出一把,用它打开了门
(D)抛掷一枚普通的正方体段子,掷得的数不是奇数就是偶数
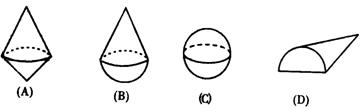
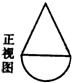
9.下列左边的正视图和俯视图对应右边物体中的
 | |||||
 | |||||
 | |||||
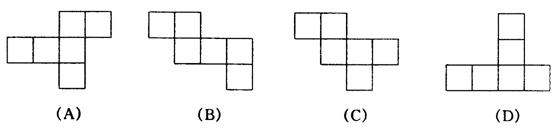 10.下列图形中,不可能围成正方体的是
10.下列图形中,不可能围成正方体的是
二、填空题(本大题共8小题,每小题2分,共16分)
11.某天早晨的气温是―7℃,中午上升了11℃,则中午的气温是_________℃。
12.把多项式2x2+3x3―x+5x4―1按字母x降幂排列是_______________________。
 13.已知∠α的补角为120°,则∠α的余角为__________。
13.已知∠α的补角为120°,则∠α的余角为__________。
14.若(a―2)2+b+1=0,则a+b3=____________。
15.有资料表明,被称为“地球之肺”的森林正以每年
公顷的速度从地球上消失,每年森林的消失量用科学记数法表
示应是_____________公顷。
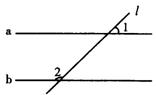
16.如图,直线L与直线a、b相交,a∥b,且∠1=45°,则∠2=_____°。
17.布袋里有两个除颜色外完全相同的球,1个红球,1个白球,把球搅匀,每次从布袋中模出一个球,如果进行10次实验,有7次出现白球,那么出现红球的频率是_______。
18.如图(1),共有1个小立方体,其中1个看得见,0个看不见;
如图(2),共有8个小立方体,其中7个看得见,1个看不见;
如图(3),共有27个小立方体,其中19个看得见,8个看不见……
则第(6)个图中,看不见的小立方体有____________个。

三、解答题(本大题共12小题,共64分。解答应写出必要的计算过程、推演步骤或文字说明。)
19.计算:(![]() ―
―![]() )×36―(―3)2。 (本题4分)
)×36―(―3)2。 (本题4分)
20.先化简,再求值:2x2y―(3xy2―5x2y+4xy2),其中x=1,y=―1。 (本题5分)
21.已知代数式2x2―3x+2的值为3。
(1)求2x2―3x的值;
(2)求6x2―9x―7的值。 (本题5分)
22.如图,C为线段AB的中点,D为线段CB的中点,若CD=2cm,求AD的长。
![]() (本题5分)
(本题5分)
23.下面每个袋(用第1行五个方框表示)中各有10个除颜色外形状、大小都相同的球。从每个袋中任意摸一个球出来,摸到白球的可能性如何?请用连线将每个袋子与第2行五个 方框的描述连起来。(本题5分)
10个白球 一个白球9个红球 5个白球5个黄球 9个白球1个红球 10个黄球
可能 不可能 不太可能 很可能 必然能
24.如图,完成下列填空:
(1)若∠1=∠B,
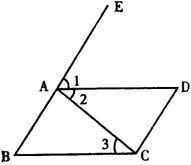 则根据_________________________________,
则根据_________________________________,
可得_______∥___________;
(2)若∠D+∠BAD=180°,
则根据_________________________________,
可得_______∥___________;
(3)若_______∥___________,
则根据_________________________________,
可得∠2=∠3。 (本题6分)
25.解方程:![]() ―
―![]() =1。(本题5分)
=1。(本题5分)
26.(1)观察图1、图2、图3,分别说出每张图中各有几条线段;
![]()
![]()
![]()
图1 图2 图3
(2)有6位科学家参加学术会议,见面时他们都互相握一次手,则他们一共握了多少次 手?(只要说出答案,不必说明理由。本题5分)
27.(1)如图1,∠AOB、∠COO都是直角,猜想:∠AOC与∠DOB在数量上是相等、互余还是互补?请说明理由;
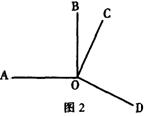
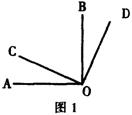 (2)图1中的∠COD绕着点O旋转,比如旋转到图2的位置,你在题(1)中的猜想仍成 立吗?为什么? (本题6分)
(2)图1中的∠COD绕着点O旋转,比如旋转到图2的位置,你在题(1)中的猜想仍成 立吗?为什么? (本题6分)
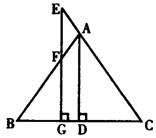 28.如图,已知ΔABC,E在CA延长线上,EG⊥BC于G,
28.如图,已知ΔABC,E在CA延长线上,EG⊥BC于G,
AD⊥BC于D,若AD平分∠BAC,∠BFG=36°,
试求∠FEA的度数。 (本题6分)
29.某种衣服,商店先按进价的3倍标价,为了吸引消费者,再按7折销售,此时每件可获利330元。问:这种衣服每件的进价为多少元? (本题6分)
30.某区举办冬季三项比赛活动,参加决赛的市民有100人,根据年龄情况制成扇形统计图 和条形统计图如下:
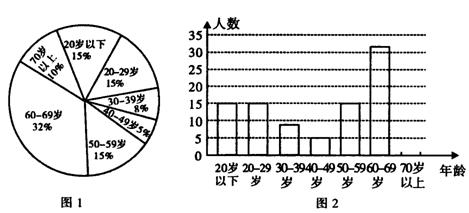 |
(1)根据图1提供的信息补全图2;
(2)上述统计图给我们提供了哪些信息(至少写出2条)? (本题6分)
2004—2005年度第一学期初一数学期末试卷参考答案及评分标准
一、1.D 2.A 3.B 4.C 5.B 6.B 7.C 8.D 9.B 10.D
二、11.4 12.5x4+3x3+2x2―x―1 13.30° 14.1 15.1.5×107
16.135° 17.![]() (或30%) 18.125(或53)
(或30%) 18.125(或53)
三、19.原式=12―18―9 (3’) =―15 (1’)
20.原式=2x2y―3xy2+5x2y―4xy2 (2’) =7x2y―7xy2 (1’)
当x=1,y=―1时, 原式=7×l×(―1)―7×1×(―1)2 (1’) =―14 (1’)
21.(1)∵2x2―3x+2=3, ∴2x2―3x=1。 (2’)
(2)6x2―9x―7=3(2x2―3x)―7 (1’) =3×1―7 (1’) =―4 (1’)
22.∵CD=2cm,D为CB的中点, ∴BC=2×2=4cm。 (2’)
∵C为AD中点, ∴AC=BC=4cm。 (2’) ∴AD=AC+CD=4+2=6cm。 (1’)
23.(每对1条线得1分)
10个白球 一个白球9个红球 5个白球5个黄球 9个白球1个红球 10个黄球

可能 不可能 不太可能 很可能 必然能
24.(1)同位角相等,两直线平行 (1’) AD∥BC (1’)
(2)同旁内角互补,两直线平行 (1’) EB∥DC (1’)
(3)AD∥BC (1’) 两直线平行,内错角相等 (1’)
25.3(x+1)―2(5―x)=6 (2’) 3x+3―10+2x=6 (1’)
5x=13 (1’)
x=![]() (1’)
(1’)
26.(1)图1中有3条线段, (1’) 图2中有6条线段, (1’) 图3中有10条线段。 (1’)
(2)一共握了15次手。 (2’)
27.(1)∠AOC=∠DOB。 (1’)
∵∠AOB=∠COD=90°, ∴∠AOB―∠BOC=∠COD一∠BOC。 即∠AOC=∠DOB。 (2’)
(2)仍成立。 (1’)
∵∠AOB=∠COD=90°, ∴∠AOB+∠BOC=∠COD+∠BOC。即∠AOC=∠DOB。 (2’)
28.∵EG⊥BC,AD⊥BC, ∴∠EGC=90°,∠ADC=90°。 (1’)
∴∠EGC=∠ADC。 ∴EG∥AD。 (1’) ∴∠FEA=∠DAC,∠BFG=∠BAD。 (2’)
∵AD平分∠BAC, ∴∠BAD=∠CAD。 ∴∠FEA=∠BFG (1’)
又∠BFG=36°, ∴∠FEA=36°。 (1’)
29.设这种衣服每件的进价为x元, (1’)
则 3x·70%―x=330 (2’) 解之,得:x=300。 (2’)
答:这种衣服每件的进价为300元。 (1’)
30.(1)补全图。 (2’)
(2)只要合理,每写对1条得2分,最多得4分。若大于2条;但有错,酌情扣分。
比如,参加决赛的人数中,60—69岁的人数最多;40~49岁的人数最少;20岁以下与20~29岁的人数相等;70岁以上高龄的人也不甘落后;从这次活动可以看出该区的体育事业蓬勃发展,等等。