典型例题
例1 判断下列各式是否正确,如不正确,请改正.
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]()
(5)![]()
(6)![]()
分析:本例旨在考察同类项概念及合并同类项的法则.
解:(1)不正确.改为![]()
(2)不正确,改为![]()
(3)不正确,此题不能合并同类项;
(4)不正确,改为![]() ;
;
(5)不正确,此题不能合并同类项;
(6)正确.
例2 合并下列多项式中的同类项:
(1)![]()
(2)![]()
解:(1)![]()
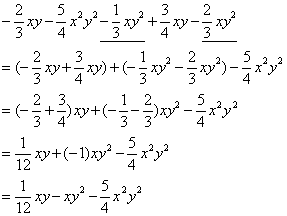
(2)原式=![]()
![]()
说明:(1)合并同类项时,一定注意不要漏项.(2)多项式合并同类项后所得结果一般按某个字母升(降)幂排列;当结论中含有多个字母时,字母的与次序最好按照它在英文字母表中的排列顺序写.
例3 化简![]()
分析:可把![]() 看作是一个字母因式,则
看作是一个字母因式,则![]() 和
和![]() 是同类项,
是同类项,![]() 和
和![]() 是同类项.
是同类项.
解:原式![]()
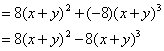
例4 求下列多项式的值:
(1)![]() ,其中
,其中![]() .
.
(2)![]()
![]()
,其中![]()
分析:由于上述两个多项式中都有同类项,所以应先合并同类项,化简多项式,然后把未知数的值代入化简后的多项式中,求出原多项式的值.
解:(1)原式=![]()
![]()
当![]() 时,原式=
时,原式=![]() .
.
(2)原式=![]()
![]()
=![]()
当![]() 时
时
原式=![]()
![]()
=![]()
=-51.
说明:如果直接把未知数的值代入多项式,进行有理数的混合运算,既麻烦,又容易出错,所以对此类题处理的一般方法是先化简,再求值,这样往往能简化运算过程.
例5 判断下列各组是不是同类项:
(1)![]() 与
与![]() ;
(2)
;
(2)![]() 与
与![]() ;
;
(3)![]() 与
与![]() ;
(4)
;
(4)![]() 与15;
与15;
(5)![]() 与
与![]() ;
(6)
;
(6)![]() 与
与![]() ;
;
(7)4与![]() .
.
分析: 根据同类项定义进行判断.同类项应所含字母相同,并且相同字母的指数与相同.二者缺一不可,与其系数无关,与其字母顺序无关.(1)题相同字母的指数不同;(2)题所含字母不同;(3)题将![]() 看作一个整体;(7)题所含字母不同.
看作一个整体;(7)题所含字母不同.
解:(3)(4)(5)(6)是同类项.
(1)、(2)、(7)不是同类项.
例6 如果![]() 与
与![]() 是同类项,求
是同类项,求![]() 的值.
的值.
分析: 欲求![]() 的值,应先求出
的值,应先求出![]() 、
、![]() 的值,由同类项的定义可知,
的值,由同类项的定义可知,![]() ,于是可求
,于是可求![]() 、
、![]() 从而可求出
从而可求出![]() 的值.
的值.
解:∵ ![]() 与
与![]() 是同类项.
是同类项.
∴ ![]()
∴ ![]() .
.
∴![]() .
.
例7 合并下列各式中的同类项
(1)![]() ;
;
(2)![]() .
.
分析: 分别把![]() ,
,![]() ,
,![]() 看作一个字母,如
看作一个字母,如![]() ,
,![]() .那么以上代数式分别化为:
.那么以上代数式分别化为:
![]()
再应用合并同类项就是十分自然的事了.
解:(1)![]()
![]()
![]()
(2)![]()
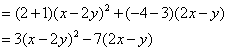
说明: 在一定的条件下,把一个代数式看作一个字母,一个复杂的代数式就会变得比较简单,使公式、法则有更广泛的应用.
例8 合并下列各式的同类项
(1)![]()
(2)![]()
分析: 把![]() 分别看作一字母,因为
分别看作一字母,因为![]() ,所以
,所以![]() ,
,![]() ,类似地有:
,类似地有:![]() .
.![]()
解:(1)![]()
![]()
![]()
![]()
(2)![]()
![]()
![]()
![]() .
.
说明: ![]() 与
与![]() 不是同类项不能合并.
不是同类项不能合并.
习题精选
一、选择题
1.下列合并同类项正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.把多项式中![]() 中的同类项分别结合在一起,应为( )
中的同类项分别结合在一起,应为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.下列各组中,不是同类项的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.130与![]() D.
D.![]() 与
与![]()
4.若A是五次多项式,B也是五次多项式,则![]() 一定是( )
一定是( )
A.五次多项式 B.十次多项式
C.不高于五次的多项式 D.单项式
二、填空题
1.请写出三个与![]() 是同类项的单项式________.
是同类项的单项式________.
2.若![]() 与
与![]() 是同类项,则
是同类项,则![]()
3.当![]() 时,多项式
时,多项式![]() 中不含
中不含![]() 项.
项.
4.九个连续整数,中间的一个数为![]() ,这九个整数的和为_____.
,这九个整数的和为_____.
三、解答题
1.对于任意正整数![]() ,下列各题的两个式子是不是同类项?为什么?
,下列各题的两个式子是不是同类项?为什么?
(1)![]() 与
与![]()
(2)![]() 与
与![]()
(3)![]() 与
与![]()
(4)![]() 与
与![]()
(5)![]() 与
与![]()
2.已知![]() 与
与![]() 是同类项,求
是同类项,求![]() 的值.
的值.
3.合并下列各式中的同类项:
(1)![]()
(2)![]()
(3)![]()
(4)![]() .
.
4.求下列各式的值.
(1)![]() ,其中
,其中![]() ;
;
(2)![]() ,其中
,其中![]() 为正整数,
为正整数,![]()
5.合并下列各式中的同类项
(1)![]()
(2)![]()
6.已知![]() ,求代数式
,求代数式![]() 的值.
的值.
7.解方程:
(1)![]() (2)
(2)![]()
8.把![]() 当作一个因式,合并
当作一个因式,合并![]() 中的同类项.
中的同类项.
9.已知![]() 与某一个单项式的和为
与某一个单项式的和为![]() ,求这个单项式.
,求这个单项式.
10.如果关于x的多项式![]() 的值与x的取值无关,求m,n的值.
的值与x的取值无关,求m,n的值.
11.已知![]() ,
,![]() ,求
,求![]() 的值,若把已知条件变为:
的值,若把已知条件变为:![]() 能求出上式的值吗?
能求出上式的值吗?
参考答案:
一、1.C 2.B 3.A 4.C
二、1.略 2.2,2 3.![]() 4.
4.![]()
三、1.(1)不是;(2)是;(3)是;(4)是;(5)是
2.4
3.(1)![]() ;
(2)
;
(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() .
.
4.(1)-4; (2)-2
5.(1)![]() (3)
(3)![]()
6.![]()
![]() 原式=1
原式=1
7.(1)![]() (2)
(2)![]()
8.![]()
9.![]()
10.合并同类项,得:![]()
![]()
![]() ∴
∴![]()
![]()
11.合并同类项,得:![]() 由
由![]() 可得
可得![]()
![]()