七 年 级 （下）数 学 期 末 练 习 卷
班级________姓名________
一.选择题（每小题3分，计30分）
1、若代数式7—2x和5—x的值互为相反数，则x的值为（ ）
A． 4 B．
2 C． 
D． 
2、如图，AB∥ED，则∠A＋∠C＋∠D＝（ ）
A．180° B．270° C．360° D．540°
3、下列条件中，不能判定三角形全等的是 （ ）
A．三条边对应相等 B．两边和一角对应相等
C．两角的其中一角的对边对应相等 D．两角和它们的夹边对应相等
4、小明用一枚均匀的硬币试验，前7次掷得的结果都是下面向上，如果将第8次掷得下面向上的概率记为P，则 （ ）
A．P=1/2 B．P＜1/2 C．P＞1/2 D．无法确定
5、已知三角形的三边分别为2，
，4那么
的取值范围是（ ）
A．
B．
C．
D．
6、在一个三角形，若
，则
是（ ）
A．直角三角形 B．锐角三角形 C．钝角三角形 D．以上都不对
7、一辆汽车以平均速度60千米/时的速度在公路上行驶，则它所走的路程s（千米）与所用的时间t（时）的关系表达式为（ ）
A．
B．
C．
D．
8、正五边形的对称轴共有（ ）
A．2条 B． 4条 C．5条 D．无数条
9、等腰三角形的一边等于3，一边等于6，则它的周长等于（ ）
A．12 B．12或15 C．15或18 D．15
10、下列图案是我国几家银行的标志，其中轴对称图形有 （ ）
A．1个 B．2个 C． 3个 D．4个
二．填空题（每小题3分，计30分）
1、多项式3a2 b
+ 2b 
–1第三项的系数是____________，次数是____________.
2、等腰三角形一个底角为36°，则此等腰三角形顶角为___________。
3、以下四个事件，它们的概率分别为多少，填在后面的横线上。
事件A：在一小时内，你步行可以走80千米，则P（A）=＿＿＿；
事件B：一个普通的骰子，你掷出2次，其点数之和大于10，则P（B）=＿＿＿；
事件C：两数之和是负数，则其中必有一数是负数，则P（C）=＿＿＿。
4.为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做的道理是 ．
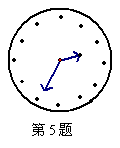
５、小芳在镜子里看镜子对面钟表的示数为2∶35 ，如图，你能确定准确时间是
６、如图，已知DE是AC的垂直平分线，AB=10，BC=11，则ΔABD的周长为＿＿＿。
 | |||||
 | |||||
 | |||||
７、如图，∠A=20
，∠C=40
，∠ADB=80，则∠ABD=＿＿＿，∠DBC=＿＿＿，图中共有等腰三角形＿＿＿个。
8、一根竹竿长3.649米。精确到十分位是 米；银原子的直径为0 .0003微米，相当于 米
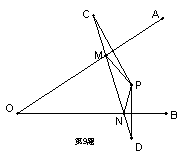
9、如图，点P关于OA、OB的对称点分别为C、D，连结CD，交OA于M，交OB于N，若
PMN的周长=8厘米，则CD为 ＿＿＿厘米。
10、如果 ，那么 的值是________
三、解答题（（1）（2）每小题5分，（3）（4）每小题6分，共22分）
（1）2（m＋1）2－(2m＋1)(2m－1) （2 ）
（3）
，其中
（4）如图，直线AC∥DF，C、E分别在AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他有没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF。以下是他的想法，请你填上根据。
小华是这样想的：
因为CF和BE相交于点O，
根据 得出∠COB＝∠EOF；
而O是CF的中点，那么CO＝FO，又已知 EO＝BO，
根据 得出⊿COB≌⊿FOE，
根据 得出BC＝EF，
根据 得出∠BCO＝∠F，
既然∠BCO＝∠F，根据 出AB∥DF，
既然AB∥DF，根据
得出∠ACE和∠DEC互补。
四、图象题（本题8分）
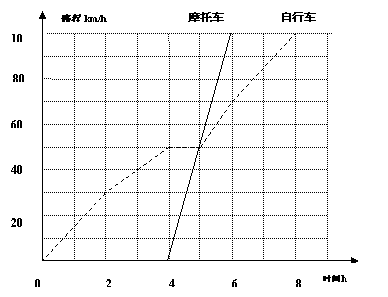
1、甲、乙两人（甲骑摩托车，乙骑自行车）从A城出发到100千米处的B城旅游，如右图表示甲、乙两人离开A城路程与时间之间的关系图象。
（1）分别求出甲、乙两人这次旅程的平均速度是多少？
（2）根据图象，你能得出关于甲、乙两人旅行的那些信息？
（至少提供三条相关信息，如由图象可知，乙比甲早出发4小时（或甲比乙晚出发4小时）等；不要再提供（1）列举的信息。）
五．探究及应用.(共30分)
1、
（1）（3分）比较左、右两图的阴影部分面积，可以得到乘法公式 （用式子表达）
（2）运用你所得到的公式，计算下列各题：（每题4分）
①
②
2、计算下列各式，：（8分）
(x-1)(x+1)=__________； (x-1)(x2+x+1)=____________；
(x-1)(x3+x2+x+1)=_______________；
……
根据以上的计算的规律，请你写出(x-1)(xn+xn-1+……x+1)等于什么？（其中n为正整数）
3、（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A＝30°，则∠ABC＋∠ACB＝ 度，∠XBC＋∠XCB＝ 度；（4分）
（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C，那么∠ABX＋∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX＋∠ACX的大小． （7分）
