第五章 《三角形》测试试卷
班级 姓名 学号
一、选择题
1．在下列长度的四根木棒中，能与4cm、9cm长的两根木棒钉成一个三角形的是（ ）．
（A）4cm （B）5cm （C）9cm （D）13cm
2．在下图中，正确画出AC边上高的是 （ ）．
（A） （B） （C） （D）
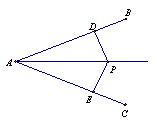3．如图，PD⊥AB，PE⊥AC，垂足分别为D、E，且PD＝PE，则△APD与△APE全等的理由是
（ ）．
（A）SAS （B）AAS
（C）SSS （D）HL
4．已知ΔABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=3∠A，则此三角 （ ）
A、一定有一个内角为45° B．一定有一个内角为60°
C．一定是直角三角形 D．一定是钝角三角形
5．在下列条件中：①∠A+∠B=∠C，②∠A∶∠B∶∠C=1∶2∶3，③∠A=900－∠B，④∠A=∠B=∠C中，能确定△ABC是直角三角形的条件有 （ ）
A、1个 B、2个 C、3个 D、4个
6．在下列条件中，不能说明△ABC≌△A’B’C的是 （ ）．
（A）∠A＝∠A’，∠C＝∠C’，AC＝A’C’ （B）∠A＝∠A’，AB＝A’B’，BC＝B’C’
（C）∠B＝∠B’，∠C＝∠C’，AB＝A’B’ （D）AB＝A’B’， BC＝B’C，AC＝A’C’
7．在下列说法中，正确的有 （ ）．
①三角对应相等的两个三角形全等 ②三边对应相等的两个三角形全等
③两角、一边对应相等的两个三角形全等 ④两边、一角对应相等的两个三角形全等
（A）1条 （B）2条 （C）3条 （D）4条
8．如果一个三角形的三条高所在直线的交点在三角形外部，那么这个三角形是 ( )．
（A）锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D)等边三角形
二、填空题
1．为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做的道理是 ．
2．一个等腰三角形的两边长分别是4 cm和6 cm，则它的周长是_____cm.
3. 如果一个三角形的两个内角是20°、30°，那么这个三角形是 三角形．
4. 直角三角形两个锐角的平分线所构成的钝角等于_____ 度。
5.如图，△ABD≌△ABC，∠C＝100°，∠ABD＝30°，
那么 ∠DAB＝ °．
6.完成下面的推理：如图，
（1）在△ABC与△A’B’C’中，
∴△ABC≌△A’B’C’(SAS)．
（2）在△ABC与△A’B’C’中，
∴△ABC≌△A’B’C’(AAS)．
7.在△ABC与△A’B’C’中，AB＝A’B’，∠A＝∠A’，要说明△ABC≌△A’B’C’，还需要增加条件 ．
8.在△ABC中,AD是BC边上的中线，写出你得到的相关结论
．
三、操作与解释
1. 如图，在△ABC中，ÐBAC是钝角，完成下列画图，并用适当的符号在图中表示；
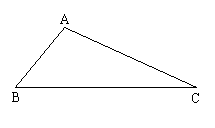⑴ ÐBAC的平分线；
⑵ AC边上的中线；
⑶ AC边上的高；
⑷ AB边上的高．
2．沿虚线，画出四种不同的图案，分别将下面的正方形划分成两个全等的图形．
3．初一(1)班的篮球拉拉队同学，为了在明天的比赛中给同学加油助威，提前每人制作了一面同一规格的三角形彩旗．小明放学回家后，发现自己的彩旗破损了一角，他想用彩纸重新制作一面彩旗．
（1） 请你帮助小明，用直尺与圆规在彩纸上作出一个与破损前完全一样的三角形；
（2） 解释你作图的理由。
四、观察与比较
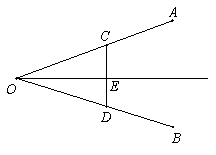
1. 如图AB、CD相交于点O，AO＝BO，AC∥DB。那么OC与OD相等吗？说明你的理由。 
2．已知：如图，在△ABC中，∠BAC=800，AD⊥BC于D，AE平分∠DAC，∠B=600；
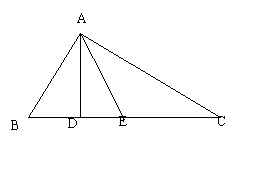（1）求∠AEC的度数.
（2）想一想，还有其它的求法吗？写出你的思考．
3．没有量角器，利用刻度尺或三角板也能画出一个角的平分线吗？下面是小彬与小红的做法，他们的画法正确吗？请说明理由．
(1) 小彬的做法
如图1，角平分线刻度尺画法：
①利用刻度尺在∠AOB 的两边上，分别取OD＝OC．
②连结CD，利用刻度尺画出CD的中点E．
③画射线OE．所以射线OE为∠AOB的角平分线．
图1
(2) 小红的做法
如图2，角平分线三角板画法：
①利用三角板在∠AOB 的两边上，分别取OM＝ON．
②分别过M、N画OM、ON的垂线，交点为P．
③画射线OE．
所以射线OP为∠AOB的角平分线．
图2
五、探究与思考
1．（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A＝30°，则∠ABC＋∠ACB＝ 度，∠XBC＋∠XCB＝ 度；
（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C，那么∠ABX＋∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX＋∠ACX的大小．
图1 图2
2．（1）如图1，AC、BD交于点E，给出怎样的两个条件，可以说明△ADE≌△BCE？为什么？
（2）如图2，在△ABC与△BAD中，给出怎样的两个条件，可以说明△ADE≌△BCE？为什么？
图1
图2
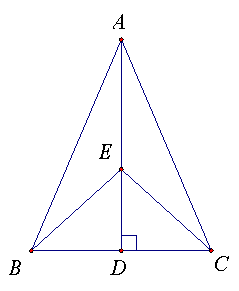
3．如图，在△ABC中，AB＝AC，点E在高AD上，找出图中全等的三角形，并简要说明它们为什么全等？