七年级综合复习数学试题
姓名 得分
一、选一选(下列各题中，只有一个正确的答案，每题3分，本题共18分)
1.不等式6-2x＜0的解集在数轴上表示为( )
2.下列多项式中，不能运用公式进行分解因式的是( )
A.
B.a4+b2
3.在
，
，
，
这几个等式中，从左到右的变形一定正确的有( )
A.1个 B.2个 C.3个 D.4个
4．若
，则下列式子正确的是( )
A. 
B. 
C. 
D. 
5.下列说法正确的是( )
A.所有的等腰三角形都相似 B.四个角都是直角的两个四边形一定相似
C.所有的正方形都相似 D.四条边对应成比例的两个四边形相似
6.调查某班级的学生对数学老师的喜欢程度，下列最具有代表性的样本是( )
A.调查单数学号的学生 B.调查所有的班级干部
C.调查全体女生 D.调查数学兴趣小组的学生
二、填一填(每空3分，本题共27分)
7.若分式
有意义，则x满足的条件是_______________.
8.分解因式：m2(x-y)+4n2(y-x)=_________________________.
9.若
10.若不等式
11.如图，在△ABC中，EF∥BC，AE=2BE，则△AEF与梯形BCFE的面积比为___________.
12.下列调查中，___________适宜使用抽样调查方式，___________适宜使用普查方式.(只填相应的序号)①张伯想了解他承包的鱼塘中的鱼的生长情况；②了解全国患非典型性肺炎的人数；
③评价八年十班本次期末数学考试的成绩；④张红想了解妈妈煲的一锅汤的味道.
13.100个数据分成5组，其中第一、二小组的频率之和等于0.11，第四、五小组的频率之和等于0.27，则第三小组的频数等于_______________.
14.命题“同角的余角相等”的条件是___________________________________________，结论是_______________________________.
15.在人体躯干和身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618越给人以美感.
三、算一算(每题6分，本题共18分)
16.求不等式 的最大整数解
17.化简求值:
其中a=1，b=-2.
18.解方程：
四、做一做(19题７分，20、21题９分本题共2５分)
19.如图，已知AB∥ED，∠1=35°，∠2=80°，求∠ACD的度数.
20、（10分）如图，梯形ABCD中，AB∥DC，∠B=
，E为BC上一点，且AE⊥ED，若BC=12，DC=7，BE：EC=1：2，求AB的长
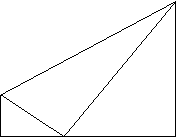Ｄ
A
Ｂ Ｅ Ｃ
21.某校八年一班的一节数学活动课安排了测量操场上悬挂国旗的旗杆的高度.甲、乙、丙三个学习小组设计的测量方案如图所示：甲组测得图中BO=
六、想一想(每题8分，本题共16分)
22.随着IT技术的普及，越来越多的学校开设了微机课.某初中计划拿出72万元购买电脑，由于团体购买，结果每台电脑的价格比计划降低了500元，因此实际支出了64万元.学校共买了多少台电脑？若每台电脑每天最多可使用4节课，这些电脑每天最多可供多少学生上微机课？(该校上微机课时规定为单人单机)
23.某工艺品厂的手工编织车间有工人20名，每人每天可编织5个座垫或4个挂毯.在这20名工人中，如果派x人编织座垫，其余的编织挂毯.已知每个座垫可获利16元，每个挂毯可获利24元.
(1)写出该车间每天生产这两种工艺品所获得的利润y(元)与x(人)之间的函数关系式；
(2)若使车间每天所获利润不小于1800元，最多安排多少人编织座垫？
七、试一试(每题8分，本题共16分)
24.已知：D是△ABC中BC边上的一点，AB=
25.为了迎接奥运，某市教育局要举办中学生体育知识竞赛.在大赛之前红光中学和育英中学先举办了一次对抗赛，每所学校各选派10人参赛，两校代表队取得的成绩如下表所示：
| 竞赛成绩(分) | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 红光中学代表队(人) | 2 | 1 | 2 | 1 | 0 | 3 | 0 | 1 |
| 育英中学代表队(人) | 1 | 2 | 1 | 1 | 3 | 1 | 1 | 0 |
(1)分别计算两队平均成绩；(2)分别计算两队的极差和方差；(3)这两个队的成绩各有什么特点？(4)你认为哪个队的团体赛的成绩会好一些？个人比赛中，哪个队的队员夺冠的可能性更大？请说明理由.
参考答案及评价标准：
(如有其它正确答案请参照相应的标准执行)
一、选一选(每题2分，本题共12分)
1.C 2.D 3.B 4.B 5.C 6.A
二、填一填(每空2分，本题共22分)
7.
8.(x-y)(m+2n)(m-2n) 9.-12 10.a≤0 11.4:5
12.①④，②③ 13.62 14.两个角是同角的余角，这两个角相等 15.7.5
三、画一画(本题共5分)
16.利用位似图形方法作图正确得3颗★，
写出结论：则以C为端点的“
”即为所求得1颗★，共4颗★
四、算一算(每题5分，本题共15分)
17. 
解：6-4(2-x)＜3(x-3)
解得x＜-7
所以x的最大整数解为x=-8
18.解：
=a-b-a-b+a2-b2
=a2-b2-2b
将a=1，b=-2代入，原式=12-(-2)2-2×(-2)=1
19.解：方程两边都乘以x(x-1)，
得3x-(x+2)=0
解得x=1
检验：将x=1代入x(x-1)=0
所以x=1是增根
所以原方程无解
五、做一做(每题6分，本题共18分)
注：20、21题因为分数有限，每步推理后的注明理由不列入评价之中；证明过程中，只要推理严谨，结论正确，即可得满分.但在数学中应尽量要求学生注明理由，说明其依据的合理性.
20.证明：∵∠DCB是△DCE的一个外角(外角定义)，
∴∠DCB＞∠CDE(三角形的一个外角大于任何一个和它不相邻的外角)
∵∠ADB是△BCD的一个外角(外角定义)，
∴∠ADB＞∠DCB(三角形的一个外角大于任何一个和它不相邻的外角)
∴∠ADB＞∠CDE(不等式的性质)
21.证法一：过C点作CF∥AB，
则∠1=∠ACF=35°(两直线平行，内错角相等)
∵AB∥ED，CF∥AB(已知)，
∴CF∥ED(平行于同一直线的两直线平行)
∴∠FCD=180°-∠2=180°-80°=100°(两直线平行，同旁内角内角互补)
∴∠ACD=∠ACF+∠FCD=35°+100°=135°
证法二：延长DC交AB于F
∵AB∥ED(已知)，
∴∠BFC=∠2=80°(两直线平行，内错角相等)，
∵∠ACF=∠BFC-∠1=80°-35°=45°
(三角形一个外角等于它不相邻的两个内角的和)
∴∠ACD=180°-∠ACF=180°-45°=135°(1平角=180°)
证法三：延长AC、ED交于F
∵AB∥ED，∴∠DFC=∠1=35°
∵∠CDF=180°-∠2=180°-80°=100°
∴∠ACD=∠CDF+∠DFC=100°+35°=135°
22.选择甲组方案计算：
解：在△ABO和△CDO中，因为∠ABO=∠CDO=90°，∠COD=∠AOB，
所以△ABO∽△CDO.
所以
，所以
，
又BO=60米，OD=3.4米，CD=1.7米，
即该校的旗杆为30米
选择乙组方案计算：
连AE，CF，在△ABE和△CDF中，因为∠ABE=∠CDF=90°，∠AEB=∠CFD，
所以△ABE∽△CDF.所以
，又CD=1.5米，FD=0.9米，EB=18米
所以
，即该校的旗杆为30米
选择丙组方案计算：
由FH∥BD，可得∠CFH=∠CBD，∠FCH=∠BCD，所以△CFH∽△CBD，
，
又EF∥AB，可得∠FEC=∠BAC，∠FCE=∠BCA，△CFE∽△CBA，
，
所以
又BD=90米，EF=0.2米，FH=0.6米，
，
即该校的旗杆为30米.
六、想一想(每题6分，本题共12分)
23.方法一：设学校共买了x台电脑，得
，
解得x=160
检验：将x=160代入所列方程，左=4000=右，
因此x=160是原方程的根
160×4=640(人)
答：学校共买了160台电脑，每天可供640人上课
方法二：此可设降价前每台电脑的价格为x元，则
，得x=4500
方法三：此可设降价后每台电脑的价格为x元，则
，得x=4000
24.解：(1)y=16×5x+24×4(20-x)，即y=-16x+1920
(2)根据题意，得-16x+1920≥1800
解得x≤7.5
x取整数，当x=8时，-16×8+1920=1792≯1800
所以x=7
答：若使车间每天所获利润不小于1800元，最多安排7人编织座垫.
七、试一试(每题8分，本题共16分)
25.解法一：存在
(1)假设AB边上存在点E，使△BDE∽△BCA，所以有
因为AB=6cm，BC=4cm，BD=1.5cm，所以
因为2.25＜6，即BE＜BA，即点E在BA上.
(2)除(1)外还存在点E，使△BED∽△BCA，所以
，
因为AB=6cm，BC=4cm，BD=1.5cm，所以
，
因为1＜6，即BE＜BA，即点E在AB上.
所以AB边上存在点E，使由顶点B、D、E组成的三角形与△ABC相似，
DE的长为1cm或2.25cm.
解法二：存在
(1)过D作DE∥AC交AB于E，可得△BDE∽△BCA，求得BE=2.25(cm)
因为2.25＜6，即BE＜BA，因此点E在AB上.
(2)以D为顶点作∠BDE=∠A，也可得△BED∽△BCA，求得BE=1(cm)
因为1＜6，即BE＜BA，因此点E在AB上
所以AB边上存在点E使由顶点B、D、E组成的三角形与△ABC相似，
DE的长为1cm或2.25cm.
注：①此题答对一种情况(求出一个BE的值)得适当分；
②解答过程只要合理，解题的格式不必追求统一，只要说明存在，并有求BE两个值的过程即可得满
26.解：
(1)
(2)红光队极差=35，育英队极差=30
(3)此问题答案具有开放性，只要学生说明有道理，答出两点就应得适当分数
例如：①红光代表队有潜力，红光队比育英队的最好成绩好；
②育英成员的成绩比较稳定，因为方差小；
③红光队队员成绩离散度大，队员之间差距大；
④两队的平均成绩相同；
⑤红光队成绩在90分以上的人数比育英队要多，有实力的队员多；
⑥红光队的众数为90分，育英队的众数是85分，红光队的高分数段队员比育英队多；
⑦红光队的中位数是77.5分，育英队的中位数是82.5分，育英队整体成绩比红光队好
(4)育英队，因为此队方差小，所以队员的成绩稳定，队员之间差距小；
红光队，因为红光队最好成绩要比育英队高(或最高成绩在红光队)，所以乙队队员夺冠的可能性大.