人教实验版八年级数学（上）评价性试题（五）
§13全等三角形
班级 姓名 号次
一．选择题（本题共8题，共32分）
1. 两个三角形只有以下元素对应相等，不能判定两个三角形全等的是（ ）
A. 两角和一边 B. 两边及夹角 C. 三个角 D. 三条边
2.下列各图中，不一定全等的是（ ）
A．有一个角是45°腰长相等的两个等腰三角形
B. 周长相等的两个等边三角形
C. 有一个角是100°，腰长相等的两个等腰三角形
D. 斜边和和一条直角边分别相等的两个直角三角形。
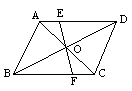
3.如图，AB∥CD，AD∥BC，OE=OF，则图中全等三角形的组数是（ ）
A. 3 B. 4 C. 5 D. 6
4.在⊿ABC和⊿A/B/C/中，AB=A/B/，∠A=∠A/，若证⊿ABC≌⊿A/B/C/还要从下列条件中补选一个，
错误的选法是（ ）
A. ∠B=∠B/ B. ∠C=∠C/ C. BC=B/C/， D. AC=A/C/，
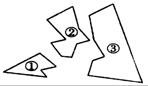5.如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
（A）带①去 （B）带②去
（C）带③去 （D）带①和②去
（6） （7） （8）
6、如图在△ABD和△ACE都是等边三角形，则ΔADC≌ΔABE的根据是（ ）
A. SSS B. SAS C. ASA D. AAS
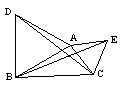
7、如图，∠1=∠2，∠C=∠D，AC、BD交于E点，下列结论中不正确的是（ ）
A. ∠DAE=∠CBE B. CE=DE C.ΔDEA不全等于ΔCBE D.ΔEAB是等腰三角形
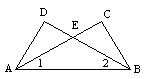
8、如图在ΔABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB=6cm，则ΔDBE的周长是（ ）
A. 6cm B. 7cm C. 8cm D. 9 cm
二、填空题（本题共8题，共32分）
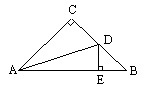
1 如图1：ΔABE≌ΔACD，AB=8cm，AD=5cm，∠A=60°，∠B=40°，则AE=_______，∠C=_____。
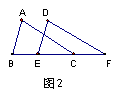
2 已知，如图2：∠ABC=∠DEF，AB=DE，要说明ΔABC≌ΔDEF
(1) 若以“SAS”为依据，还要添加的条件为______________；
(2) 若以“ASA”为依据，还要添加的条件为______________；
(3) 若以“AAS”为依据，还要添加的条件为______________；
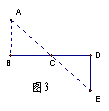
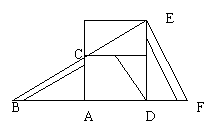
3． 如图3所示：要测量河岸相对的两点A、B之间的距离，先从B处出发与AB成90°角方向，向前走50米到C处立一根标杆，然后方向为变继续朝前走50米到D处，在D处转90°沿DE方向再走17米，到达E处，使A、C与E在同一直线上，那么测得A、B的距离为_____米。
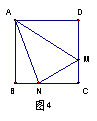
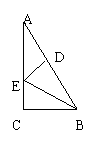
4．如图4：沿AM折叠，使D点落在BC上，如果AD=7cm，DM=5cm，∠DAM=30°，则AN=_________ cm，∠NAM=_________。
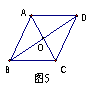
5．如图5，已知AB∥CD，∠ABC=∠CDA，则由“AAS”直接判定Δ_______≌Δ______。
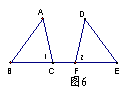
6．如图6，点C、F在BE上，∠1=∠2，BC=EF。请补充条件：__________(写一个即可)，
使ΔABC≌ΔDEF。
7如图幼儿园的滑梯中有两个长度相等的梯子（BC=EF），左边滑梯的高度AC等于右边滑梯水平方向的长度DF，则∠ABC+∠DFE= °.
8.在RtΔA BC中,BE平分∠ABC,ED⊥AB于D,若AC=3㎝,则AE+DE= ㎝.
三. 解答题：(本题共5大题,共36分)
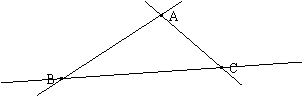
1、如图，三条公路两两相交于Ａ、B、C三点，现计划建一座综合供应中心，要求到三条公路的距离相等，则你能找出符合条件的地点吗？画出来。
 |
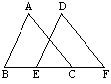2、 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.
求证: ΔCAB≌ΔDEF
 |
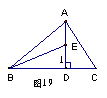3、如图，AD⊥BC于D，AD=BD，AC=BE。
(1) 请说明∠1=∠C
(2) 猜想并说明DE和DC有何特殊关系？
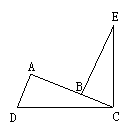4、如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC, 能否找出与AB+AD相等的线段,并说明理由.
5．如图，已知点C是AB上一点，ΔACM、ΔCBN都是等边三角形。
(1) 说明AN=MB
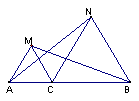(2) 将ΔACM绕点C按逆时针旋转180°，使A点落在CB上，
请对照原题图在右图画出符合要求的图形。
(3) 在(2)所得到的图形中，结论“AN=BM”是否成立？若成立，
请说明理由；若不成立，也请说明理由。
(4) 在(2)所得到的图形中，设AM的延长线与BN相交于点D，
请你判断ΔABD的形状，并说明你的理由。
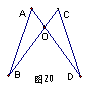
提高：如图，小明在完成数学作业时，遇到了这样一个问题，AB=CD，BC=AD，请说明：
∠A=∠C的道理，小明动手测量了一下，发现∠A确实与∠C相等，但他不能说明其中的道理，你能帮助他说明这个道理吗？试试看。
 |