人教实验版八年级数学（上）评价性试题（八）
§14 轴对称
班级 姓名 号次
一．选择题
1.下列图形中，不是轴对称图形的是 （ ）
 |
A． B。 C。 D。
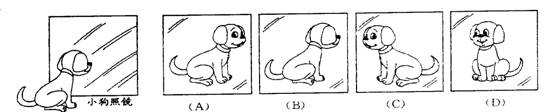2．一只小狗正在平面镜前欣赏自己的全身像（如图所示），此时，它所看到的全身像是( )
3、
下列图案是几种名车的标志，请你指出，在这几个图案中是轴对称图形的共有（ ）
A.4个； B.5个； C. 6个 ； D.7个。
4、国旗是一个国家的象征，观察下面的国旗，是轴对称图形的是（ ）
A.加拿大、哥斯达黎加、乌拉圭 B.加拿大、瑞典、澳大利亚
C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士
加拿大 哥斯达黎加 澳大利亚 乌拉圭 瑞典 瑞士
5、和点P（－3，2）关于y轴对称的点是（ ）
A.（3， 2） B.（－3，2） C. （3，－2） D.（－3，－2）
6、．一束光线从点Ａ（３，３）出发，经过ｙ轴上点Ｃ反射后经过点Ｂ（１，０）则光线从Ａ点到Ｂ点经过的路线长是（ ）
Ａ．４
Ｂ．５
Ｃ．６
Ｄ．７
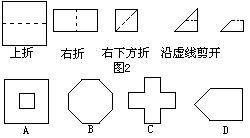
7、如图３把一个正方形三次对折后沿虚线剪下，则所得图形大致是（ ）
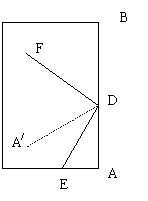
8、小朋友文文把一张长方形的对折了两次，如图所示：使A、B都落在DA/上，折痕分别是DE、DF，则∠EDF的度数为（ ）
A.60° B. 75° C. 90° D.120°
二、填空题（本题共8题，每题4分，共32分）
1、成轴对称的两个图形的对应角 ，对应边（线段）
2、在“线段、锐角、三角形、等边三角形”这四个图形中，是轴对称图形的有 个，其中对称轴最多的是
.线段的对称轴是
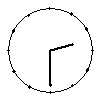
3、如图，从镜子中看到一钟表的时针和分针，此时的实际时刻是________。
4、数的计算中有一些有趣的对称形式， 如：12×231=132×21；仿照
上面的形式填空，并判断等式是否成立：
(1) 12×462=____×____ ( ) , (2) 18×891=____×____ ( )。
5、右图是跳棋盘，其中格点上的黑色点为棋子，剩余的格点上
没有棋子.我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内
沿着棋子对称跳行，跳行一次称为一步.己知点A为己方一枚棋子，欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最少步数为 步
6、在日常生活中，事物所呈现的对称性能给人们以平衡与和谐的美感. 我们的汉语也有类似的情况，呈现轴对称图形的汉字有
（请举出两个例子，笔画的粗细和书写的字体可忽略不计）.
7、已知点A（a，-2）和B（3，b），当满足条件 时，点A和点B关于y轴对称。
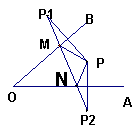
8、如图，点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于M，交OB于N，P1P2=15，则△PMN的周长为 。
三、解答题（本题共5小题，共36分）
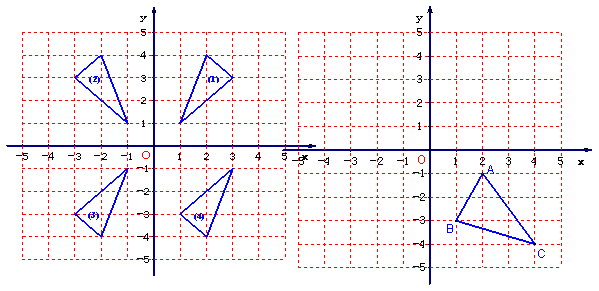
1（1）如图所示编号为①、②、③、④的四个三角形中，关于y轴对称的两个三角形的编号为 ；关于坐标原点O对称的两个三角形的编号为 ；
（2）在图4中，画出与△ABC关于x轴对称的△A1B1C1
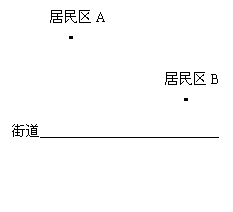
2、如图所示，要在街道旁修建一个牛奶站，向居民区A、B提供牛奶，牛奶站应建在什么地方，才能使A、B到它的距离之和最短？
 |
3、用两个圆、两个正三角形、两条线段设计一个轴对称图案，并说明你要表达的含义。
4.如图，EFGH为矩形台球桌面，现有一白球A和一彩球B.应怎样击打白球A,才能使白球A碰撞台边EF,反弹后能击中彩球B?
5、在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角。特别的，当旋转角为180度时，就称这个图形为中心对称图形。例如：正方形绕着它的对角线的交点旋转90°和180°后都能与自身重合（如图），所以正方形是旋转对称图形，也是中心对称图形。
（1）
判断下列命题的真假（在相应的括号内填上“真”或“假”）。
①等腰梯形是旋转对称图形，它有一个旋转角为180°。（ ）
② 矩形是旋转对称图形，它有一个旋转角为180°（ ）
（2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是 （写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形 。
（3）写出满足下列条件的旋转对称图形
①是轴对称图形，但不是中心对称图形：
②既是轴对称图形，又是中心对称图形：