八年级(下)第六章综合测试卷2004.5.29[fjj1]
姓名:___________ 学号:____________ 班级:____________ 得分:__________
1、△ABC中,∠B=45º,∠C=72º,那么与∠A相邻的一个外角等于 .
2、在△ABC中,∠A+∠B=110º,∠C=2∠A,则∠A= ,∠B= .
3、直角三角形中两个锐角的差为20º,则两个锐角的度数分别为 .
4、如下图左,AD、AE分别是△ABC的角平分线和高,∠B=50º,∠C=70º,则∠EAD= .

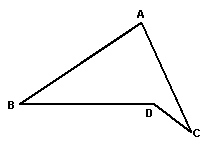
5、如上图右,已知∠BDC=142º,∠B =34º,∠C=28º,则∠A= .
6、把下列命题“对顶角相等”改写成:如果 ,那么
.
7、如下图左,已知DB平分∠ADE,DE∥AB,∠CDE=82º,则∠EDB= ,∠A=
.
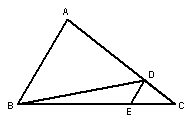
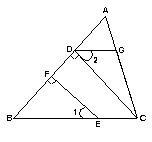
8、如上图右,CD⊥AB于D,EF⊥AB于F,∠DGC=111º,∠BCG=69º,∠1=42º,则∠2= .
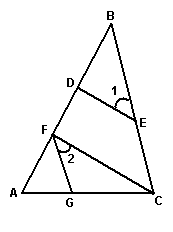
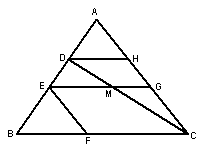
9、如下图左,DH∥GE∥BC,AC∥EF,那么与∠HDC相等的角有 .
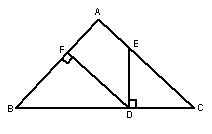
10、如上图右:△ABC中,∠B=∠C,E是AC上一点,ED⊥BC,DF⊥AB,垂足分别为D、F,若∠AED=140º,则∠C= ∠A= ∠BDF= .
11、△ABC中,BP平分∠B,CP平分∠C,若∠A=60º,则∠BPC= .
12、满足下列条件的△ABC中,不是直角三角形的是( )
A、∠B+∠A=∠C
B、∠A:∠B:∠C=2:3:5
C、∠A=2∠B=3∠C D、一个外角等于和它相邻的一个内角
13、如图,∠ACB=90º,CD⊥AB,垂足为D,下列结论错误的是( )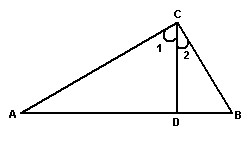
C、∠1和∠B都是∠A的余角
D、∠2=∠A
14、三角形的一个外角是锐角,则此三角形的形状是( )
A、锐角三角形 B、钝角三角形 C、直角三角形 D、无法确定
15、如下图左:∠A+∠B+∠C+∠D+∠E+∠F等于( )
A、180º B、360º C、540º D、720º

16、锐角三角形中,最大角α的取值范围是( )
A、0º<α<90º B、60º<α<90º C、60º<α<180º D、60º≤α<90º
17、下列命题中的真命题是( )
A、锐角大于它的余角 B、锐角大于它的补角
C、钝角大于它的补角 D、锐角与钝角之和等于平角
18、已知下列命题:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两直线平行;⑤邻补角的平分线互相垂直.其中,正确命题的个数为( )
A、0 B、1个 C、2个 D、3个
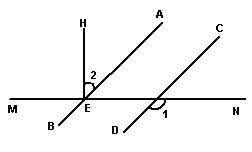
19、如上图右:AB∥CD,直线HE⊥MN交MN于E,∠1=130º,则∠2等于( )
A、50º B、40º C、30º D、60º
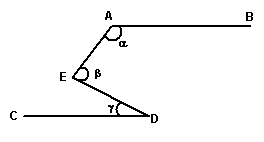
20、如图,如果AB∥CD,则角α、β、γ之间的关系式为( )
21、如图,BC⊥ED,垂足为O, ∠A=27º,∠D=20º,求∠ACB与∠B的度数.
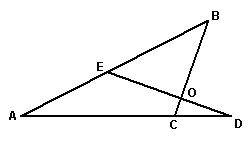
22、如图:∠A=65º ,∠ABD=∠DCE=30º,且CE平分∠ACB,求∠BEC.
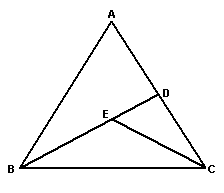
23、如图:
已知:△ABC中,∠A=∠B,CE是外角∠BCD的平分线
求证:CE∥AB
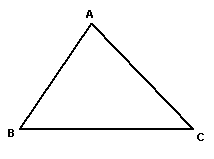
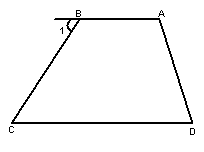
24、看图填空:
∴ ∥ ( )
∴∠1= ( )
∵∠1=65º(已知)
∴∠C=65º( )
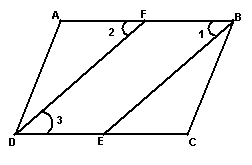
证明:∵BE、DF分别平分∠ABC、∠ADC(已知)
∴ ∠1=![]() ∠ABC,∠3=
∠ABC,∠3=![]() ∠ADC( )
∠ADC( )
∵∠ABC=∠ADC(已知)
∴![]() ∠ABC=
∠ABC=![]() ∠ADC(
)
∠ADC(
)
∴∠1=∠3( )
∵∠1=∠2(已知)
∴∠2=∠3( )
∴( )∥( )( )
∴∠A+∠ =180º ,∠C+∠ =180º( )
∴∠A=∠C( )
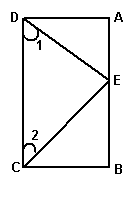
25、如图:已知CB⊥AB,CE平分∠BCD,DE平分∠ADC,∠1+∠2=90º
求证:AB∥CD
26、如图,已知:AC∥DE,DC∥EF,CD平分∠BCA
求证:EF平分∠BED.

27、如图,已知:CF⊥AB于F,ED⊥AB于D,∠1=∠2,
求证:FG∥BC