一次函数-初中二年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载

云形标注: 新课标 八年级(上)数学单元目标检测题

　　　　　　　　　　　　　　 (一次函数)

姓名:　　　　　班别:　　　　 : 座号:　　　　评分:　　　　　

一.　　选择题( 本大题共6小题, 每小题3分,共18分)

1.判断下列变化过程存在函数关系的是(　)

A.是变量,　　　　 B.人的身高与年龄

C.三角形的底边长与面积　　　　D.速度一定的汽车所行驶的路程与时间.

　2.已知函数,当时,= 1,则的值为( )

A.1　　　　　 B.-1　　　　 C.3　　　　 D.1/2

　3.下列说法正确的是( )

A.正比例函数是一次函数　　　　　　 B.一次函数是正比例函数

C.变量,是的函数,但不是的函数

D.正比例函数不是一次函数,一次函数也不是正比例函数

　4.下列函数关系式:①;②③;④.其中一次函数的个数是(　)

　　A. 1个　　　　B.2个　　　　 C.3个　　　　 D.4个

　5.在直角坐标系中,既是正比例函数,又是的值随值的增大而减小的图像是(　)

　　　 A　　　　　　　　 B　　　　　　　　 C　　　　　　　 D

　6.如图,直线经过A(0,2)和B(3,0)两点,那么

　这个一次函数关系式是(　)

　 A.　B. C. D.

二.　填空题(本大题共6小题,每题4分共24分)

　7.函数的三种表示方式分别是　　　　、　　　、　　　　。

　8.小明将RMB1000元存入银行,年利率为2%,利息税为20%,那么年后的本息和(元)与年数的函数关系式是　　　　　 .

　9.已知一次函数+3,则=　　　 .

　10.已知一次函数,函数的值随值的增大而增大,则的取值范围是　　　 .

　 11.函数中,的值随值的减小而　　　 ,且函数图像与轴、轴的交点坐标分别是　　　　　　　　 .

　 12.已知直线与轴,轴围成一个三角形,则这个三角形面积为

　　 (平方单位).

三.　解答题(本大题共6小题,共52分)

13.在同一直角坐标系上画出函数的图像,并比较它们的异同.(8^/)

文本框: (吨)

0 1 2 3 4 5 6 7 8 9 10 11 12 (月)

14.如图,这是某工厂2002年蜡烛库存量

(吨)与时间(月)关系的图像,其中年

　　初库存量为5吨.(8^/)

①根据图像写出与的函数关系式;

②根据函数关系式求6月份的库存量.

　　15.某校组织八年级的学生到动画城游乐.动画城集体门票的收费标准有两种:①50人以内(含50人),每人15元,超过50人的,超出部分,每人10元;16.②80人以内(含80人),每人13元,超过80人的,超出部分,每人10.50元.

　　　⑴分别写出两种收费标准的应收门票费(元)与游乐人数(人)( 之间的函数关系;(6^/)

⑵若该年级有220名学生去动画城游乐,如何组合才使购门票费较少?(4^/)

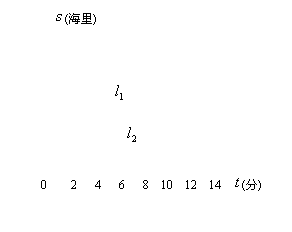
文本框: (海里)

0 2 4 6 8 10 12 14 (分) 文本框: 14
12
10
8
6
4
2 16.某港口缉私队的观测哨发现正北方6海里处有一艘可疑船只A正沿北偏东60⁰方向直线行驶, 缉私队立即派出快艇B沿北偏东45⁰方向直线追赶.下图中分别表示A,B两船的行走路线.6分钟后A,B两船离海岸分别为7,4海里.(8^/)　　　　　　　　　