第十九章 四边形检测题
一、 填空题
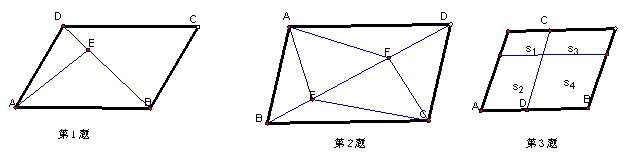
1、如图在四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE= 度。
2、如图,BD是平行四边形ABCD的对角线,度E、F在BD上,要使四边形AECF是平行四边形,还需要增加的一个条件是 (填上你认为正确的一个即可,不必考虑所有可能情形)。
3、如图,一个平行四边形被分成面积为S1、S2、S3、S4四个小平行四边形,当CD沿AB自左向右在平行四边形内平行滑动时,则S1S4与S2S3的大小关系为 。
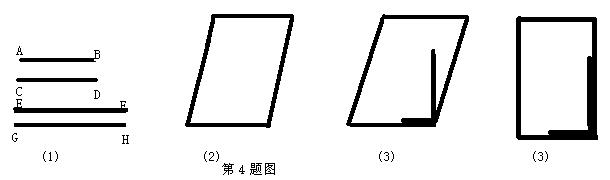
4、工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料,如图(1),使AB=CD,EF=GH;
(2)摆成如图(2)的四边形,则这时窗框的形状是 形,根据的数学道理是
(3)将直角尺靠紧窗框的一个角,如图(3),调整窗框的边框,点直角尺的两条直角边与窗框无缝隙时,如图(4),说明窗框合格,这时窗框是 ,根据的数学道理是 。
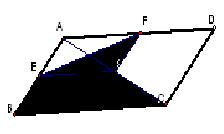
5、如图,菱形ABCD的对角线的长分别是2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交A于F,则阴影部分的面积是 。
二、选择题
6、下列命题中正确的是( )
(A)对角线互相平分的四边形是菱形 (B)对角线互相平分且相等的四边形是菱形
(C)对角线互相垂直的四边形是菱形 (C)对角线互相垂直平分的四边形是菱形。
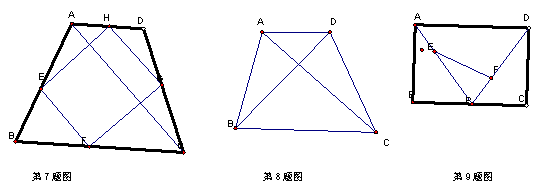
7、如图某花木场有一块等腰梯形ABCD的空地,其各边的中点分别是点E、F、G、H,测量得对角线AC=10米,现想用篱笆围成四边形EFGH场地,则需篱笆的总长度是( )
A、40米 B 30米 C 20米 D 10米
8、如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则该梯形的面积是( )
A 30 B 15 C 7.5 D 60
9、如图,已知距形ABCD,R、P分别是DC、BC上的点,E、F分别是AP、RP的中点,当P在BC上从B向C移动而R不动时,那么下列结论成立的是( )
A、线段EF的长逐渐增大 B 线段EF的长逐渐减小
C 线段EF的长不改变 D 线段EF的长不能确定
三、解答题
10、已知如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF。求证:DE=BF。

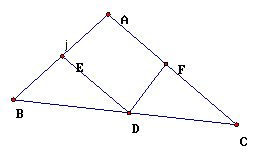
11、已知 如图,D是⊿ABC的边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE,
求证:(1) ⊿ABC是等腰三角形 (2) 当∠A=90°时,试判断四边形AFDE是怎样的四边形,证明你的判断结论。
12、探究规律
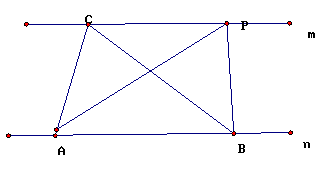
如图,已知直线m∥n,A、B为直线n上两点,C、P为直线m上的两点。
(1) 请写出图中面积相等的两对三角形
(2) 如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有
与⊿ABC的面积相等;理由是
13、解决问题
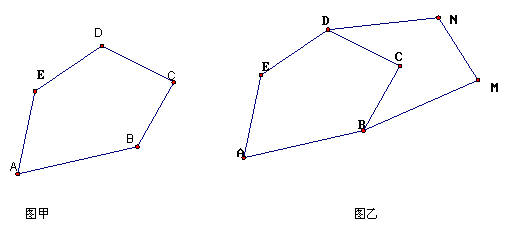
如图甲,五边形ABCDE是张大爷十年前承包的一块土地。经过多年开垦荒地,现在已变成如图乙所示的形状,但承包土地与开垦荒地的分界小路(图乙中的折线DCB)还保留着,张大爷想过E点修一条直路,直路修好后,要保持直路左边与承包时的一样多,请你用有关的几何知识,按张大爷的要求设计出修路方案(不计分界小路与直路的占地面积)
(1) 写出设计方案,并在图乙中画出相应的图形
(2) 说明方案设计理由。