2003-2004初二上学期数学期末试卷
（完卷时间120分钟）
姓名: 班级: 座号: 成绩:
A卷 100分
一、选择题（本大题共7小题，每小题3分，共21分）
1、将直角三角形三边扩大同样的倍数，得到的三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、任意三角形
2、下列各式中正确的是（ ）
A、
B、
C、
D、
3.将图形 按顺时针方向旋转900后的图形是( )
A B C D
4、下列图形中，不是中心对称图形的是（ ）
A、线段 B、矩形 C、等腰梯形 D、正方形
5.在直角坐标系中,既是正比例函数
,又是
的值随
值的增大而减小的图像是( )
A B C D
6、10名初中毕业生的中考体育考试成绩如下：25 26 26 26 26 27 28 29 29 30 ，这些成绩的中位数是（ ）
A、25 B、26 C、26.5 D、30
7、若2a2sb3s－2t与－3a3tb5是同类项，则( )
A、 s=3，t=－2 B 、s=－3，t=2 C s=－3，t=－2 D s=3，t=2
二、填空题（本大题共8小题，每小题3分，共24分）
1、三角形的三边分别为7，15，24，则这个三角形的最大角为 度.
2、 一组数据10，9，11，10，8，9，12，10的众数是 .
3、已知7，4，3，a，5这五个数的平均数是5，则a＝___________
4、p（3，－4）到原点的距离为 .
5、若点（3，n）在函数y=－2x的图像上，则n = .
6、若(2x—y—3)2+3x＋y－2=0，那么x=________，y=______.
7、已知点A（1，－2），若A、B两点关于X轴对称，则B(________)
8、某单位共有职工342人，其中男职工人数y比女职工人数x的2倍少18人，根据题意列方程组得_______________.
三、计算题（本大题共4小题，每小题6分，共24分）
1、
2、
3、
4、
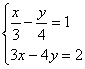
四、在同一直角坐标系内作出一次函数y＝
x＋1和y＝x－1的图像。直线y＝x＋1和直线y＝x－1的交点是 .（本题共6分）
你能据此求出方程组 y＝x＋1 的解是多少？
y＝x－1
五、如图，在□ABCD中，AC交BD于点O，点E、点F分别是OA、OC的中点，请判断线段BE、DF的关系，并证明你的结论。（本题共5分）
 |
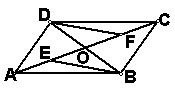六、列方程组解应用题（本题共两题，每小题7分，共14分）
1、某校初一年级(1)、(2)两个班共有96人，在一次数学测验中，(1)班的及格率为80%，(2)班的及格率为90%，而两个班的总及格率为85%，求(1)、(2)两班的人数各是多少？
2、一个两位数，个位上的数比十位上的数的3倍多2，若把个位数字与十位上的数对换所得新的两位数比原来的两位数的3倍少2，求原两位数。
七、某次歌唱比赛，三名选手的成绩如下：（本题共6分）
| 测试项目 | 测试成绩 | ||
| A | B | C | |
| 创新 | 72 | 85 | 67 |
| 唱功 | 50 | 74 | 70 |
| 综合知识 | 88 | 45 | 67 |
（1）若按三项的平均值取第一名，谁是第一名？
（2）若三项测试得分按3：6：1的比例确定个人的测试成绩，谁是第一名？
B卷（20分）
一、小明将RMB1000元存入银行,年利率为2%,利息税为20%,那么年后的本息和(元)与年数的函数关系式是
.（2分）
二、已知一次函数
+3,则
= .（2分）
三、
2x+y=5k
二元一次方程组
的解满足方程
x－2y=5，那么k的值为
2x－y=7k
( )（2分）A 
B 
C －5 D 1
四、一寺庙内不知有多少个僧人，但饭碗和汤碗364只，如果3人共用一个饭碗吃饭，4人共用一个汤碗喝汤，正好用完所有的饭碗和汤碗。问：寺庙内共有多少个僧人？（本题4分）
五、为保护学生视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为ycm，椅子的高度为xcm，则y应是x 的一次函数，下表列出两套符合条件的课桌椅的高度：（本题共4分）
| 第一套 | 第二套 | |
| 椅子高度xcm | 40.0 | 37.0 |
| 桌子高度ycm | 75.0 | 70.2 |
(1)请确定y与x的函数表达式
(2)现有一把高39cm的椅子和一张高为78.2的课桌，它们是否配套？为什么？
六、某港口缉私队的观测哨发现正北方6海里处有一艘可疑船只A正沿北偏东600方向直线行驶, 缉私队立即派出快艇B沿北偏东450方向直线追赶.下图中
分别表示A,B两船的行走路线.6分钟后A,B两船离海岸分别为7,4海里.（ 本题共6分）
①根据图像能否写出两直线的
与的函数关系,试试看;
②快艇能否追上可疑船只?若
能追上,大约需几分钟,离海岸
几海里?
