直角三角形全等的判定
福清元樵中学 林华泉
教学目标
1. 已知斜边和一直角边会作直角三角形.
2. 掌握“斜边直角边公理”,会熟练利用这个公理及一般三角形全等的判定方法判定直角三角形全等.
3. 熟练使用“分析综合法”探讨解题思路.
教学重点和难点
“斜边直角边公理”的掌握和灵活运用.
教学过程设计
一、 讨论直角三角形全等的判定方法
1.可用判定一般三角形全少的方法.
练习1 判断以下各组直角三角形是否全等,为什么?
(1) 两直角边对应相等的两个直角三角形;
(2) 一边和一锐角对应相等的两个直角三角形.
分析:(1)判定两直角三角形全等时,直角相等是一个很重要的隐含条件.
2、由于直角三角形是特殊的三角形,所以一般三角形全等的四种判定方法对直角三角形都适用.
3、由于直角三角形与一般三角形相比增加了一个特殊条件——直角,因此,判定直角三角形全等的条件可减弱到两个,“SSS”对直角三角形来说条件多余.
2.探求判定直角三角形全等的特殊方法.
(1) 对直角三角形中的两对对应元素进行分类,探求有无判定全等的其它方法.
除练习1的(1)和(2)之外,还有以下两种情况:
① 两锐角对应相等;
② 斜边和一直角边对应相等.
(2)对第①句,由教师和学生手中的含30°的直角三角板可说明它不成立,
因此,判定直角三角形全等仍然至少需要一边对应相等.
 对第②句,通过画图寻找答案.
对第②句,通过画图寻找答案.
3.画图得出公理.
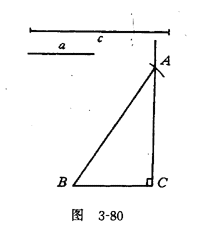
例1 如图3-80,已知线段a,c(a<c),画一个Rt△ABC,使∠C=90°,一直角边CB=a,斜边AB=c.
教师应注意启发学生选择合理的画图顺序来确定三角形的三个顶点:
画直角确定顶点C→在直角一边上截取线段a确定B点→以点B为圆心,线段c为半径作弧与另一直角边相交确定点A.
说明:(1)教师按照教材所述,详细板书画法并作图.
(2)着重说明画出的直角三角形存在且唯一,因此,可以作为判定公理,称为“斜边、直角边公理”,简写为“HL”.
4.叙述公理,强调条件及格式.
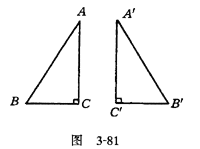
教师板书“HL公理”的内容,说明它实际上就是两边及其中一边的对角对应相等,但所对的角是直角,所以它只对直角三角形适用,对一般三角形并不一定成立,因此,在“HL公理”的使用过程中要突出直角三角形这个条件,对于图3-81,在Rt△ABC与Rt△AˊBˊC
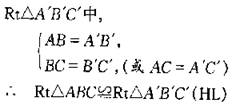
一、 应用举例
例1、 已知:如图3-82,在△ABC与△AˊBˊCˊ中,CD和CˊDˊ分别是高,并且AC=AˊCˊ,CD=CˊDˊ,∠ACB=AˊCˊBˊ.
求证:△ABC≌△AˊBˊCˊ.
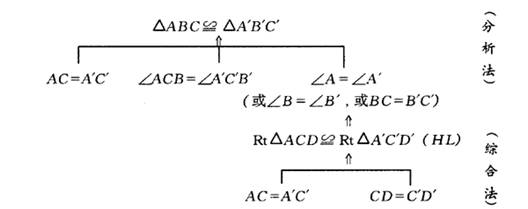
说明:请一名学生口述,教师纠正后板书正确过程.
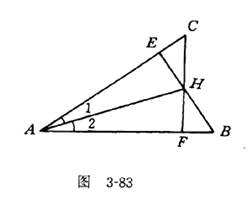
(投影)练习2 如图3-83,AB=AC,CF┵AB于F,BE┵AC于E,CF与BE交于H.求证:(1)AH平分∠ABC;(2)CH=BH;(3)AH┵BC;(4)连结BC与AH的延长线交于D,图中有多少对全等三角形?为什么?(5)交换“AB=AC”与“AH平分∠BAC”,以上命题是否成立?为什么?
说明:(1)通过二次全等证明所需结论,并培养学生逆向思维能力.
(2)通过此题全面复习直角三角形全等的判定方法(SAS,AAS,ASA,HL).
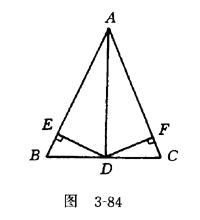
(投影)练习3 已知:如图3-84,AB=AC,AD┸BC于D,DE┸AB于E,DF┸AC于F.求证:DE=DF.
(投影)例3 求证:有一条直角边和斜边上的高对应相等的两个直角三角形全等.
说明:要求学生根据文字叙述画图,分析已知、未知条件,根据直角三角形的判定方法来证明两次全等.
三、师生共同小结
1.一般三角形与直角三角形证明全等的方法有什么区别与联系?
2.灵活选用几种方法来证明两个直角三角形全等,注意分析法与综合法的使用.
四、作业
 课本第55页第2,3,4题.
课本第55页第2,3,4题.
补充题:
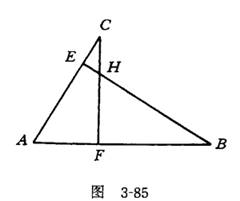
1.1. 如图3-85,A,F和B三点在一条直线上,CF┴AB于F, AF=FH, CF=FB.求证: BE⊥AC.
说明:利用三角形全等来说明两直线的垂直关系.
2.思考:两边及其中较长边所对的角对应相等的两个三角形是否全等?为什么?较短边所对的角对应相等吗?
提示:(1)对较长边所对的角按锐角、直角、钝角三种情况来进行分类讨论,结论成立.可用尺规作图作出符合条件的唯一确定的三角形.
(2)对较短边所对的角按锐角、直角、钝角三种情况进行分类讨论,发现由“大边对大角”得知直角、钝角时三角形不存在,而锐角时即为表3.1中“SSA”的反例图形,三角形形状不唯一.
课堂教学设计说明
本教学设计需1课时完成.
1.练习1是在复习巩固并运用一般三角形的四种判定方法判定直角三角形全等的基础上,让学生总结规律:直角三角形只需再加两个特定条件就能判定全等.引导学生对两个特定条件进行分类,引出对“斜边、直角边公理”的思考.
2.教师也可采用第二种引入新课的方法如下:
(1)复习一般三角形的四种判定方法.
(2)提问:SSA能否判定一般三角形全等?能否判定直角三角形全等?
(3)教师用投影演示表3.1中“SSA”的反例图形:
①分解出△ABD与△ABC;
②分别绕点A旋转AD和AC使AB所对的角都变为直角;
① ③ 对比发现,当两边及其中一边(较短边)所对的角为锐角时三角形形状不唯一;但当两边及其中一边(较长边)所对的角为直角时,直角三角形形状就唯一被确定.
(结合补充题2可对括号内边、角对应关系理解得更清楚。)
(4)猜想“SSA”可用来判定两直角三角形全等,但不称为“SSA”,而由边角对应关系称为“斜边、直角边”.
3.练习2与补充题1实际上均是“三角形三条高交于一点”的特殊化形式,如果教师能看到这类题目之间的联系,就可以灵活自由地设计一题多变的题目,在变化与联系中培养学生逻辑思维能力.
4.补充题2让程度较好的学生对“SSA”能否判定两三角形全等有一个更为深刻的认识,
以后学完正弦定理后,就能对“ SSA’问题有一个更全面深刻的认识.