初二(下)期末数学检测题(一)
一、选择：
1.
下列实数:
0．……中,无理数有( )个．
(A)2 (B)3 (C)4 (D)5
2．下列语句正确的是( )
(A) －2是－4的平方根; (B) 2是(－2)2的算术平方根;
(C) (－2)2的平方根是2; (D) 8的立方根是±2．
3．下列各数中，互为相反数的是( )
(A)－2与
；（B）-2与
；（C）-2与
；（D）
与2．
4．实数a、b、c在数轴上的位置如图:
则化简
的结果是( )
(A)a－b－c; (B)a－b+c; (C)－A+B+C; (D)－a+b－c．
5．式子
有意义的条件是( )
(A) －2≤x≤2; (B) －2≤x≤2且x≠1; (C) x>－2; (D)x≥－2且x≠1．
6．下列二次根式中,是同类二次根式的是( )
(A) 
(B)
与
；(C)
与
；(D)
与．
7．试估计
的大小范围是(
)
(A)7．5 ~ 8．0; (B)8．0 ~ 8．5; (C)8．5 ~ 9．0; (D)9．0 ~ 9．5．
8．一个多边形的每个内角都是1440,则它的边数是( )
(A) 8; (B) 9; (C)10; (D)11．
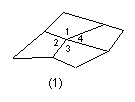
9．如图1,用一批形状和大小都完全相同但不规则的四边形地砖能
铺成一大片平整且没有空隙的平面(即平面图形的镶嵌),其原理是( )
(A)四边形有四条边; (B) 四边形有四个内角;
(C)四边形具有不稳定性;(D)四边形的四个内角的和为3600．
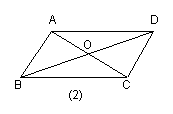
10．如图2,平行四边形ABCD的周长为40,ΔBOC的周长比
ΔAOD的周长多10,则AB为( )
(A) 20; (B) 15; (C) 10; (D)5．
11．顺次连结等腰梯形各边中点得到的四边形( )
(A) 只能是平行四边形; (B)是矩形; (C) 是菱形; (D)是正方形．
12．在等边三角形、平行四边形、矩形、菱形、正方形、等腰梯形中,既是中心对称图形又是轴对称图形,并且只有两条对称轴的有( )个
(A) 1; (B) 2; (C)3; (D)4．
13．相距125千米的两地在地图上的距离为25cm,则该地图的比例尺为( )
(A) 1∶5000; (B) 1∶50000; (C) 1∶500000; (D)1∶．
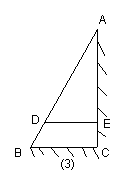14．如图3,斜靠在墙上的梯子AB,梯脚B距墙面1．6米,梯上一点D距墙面1．4米,BD长0．55米,则梯子AB的长为( )米
(A) 3．85; (B) 4．00; (C) 4．4; (D)4．50．
二、填空:
15．若三角形的三边a、b、c满足a2－4a+4+
=0,
则笫三边c的取值范围是_____________．
16．先化简再求值:当a=9时,求a+
的值,甲乙两人的解答如下:
甲的解答为:原式=a+
=a+(1－a)=1;
乙的解答为:原式=a+=a+(a－1)=2a－1=17． 两种解答中,____的解答是错误的,错误的原因是未能正确地运用二次根次的性质：_______________．
17．将对角线分别为5cm和8cm的菱形改为一个面积
不变的正方形,则正方形的边长为_______cm．
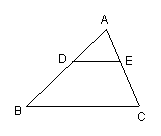
18．如图,DE∥BC,AD∶BD=2∶3,
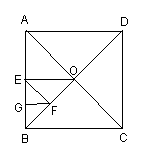则ΔADE的面积∶四边形DBCE的面积=______．
19．计算: 
=_____,
=_____,
=____;……．通过以上计算,试用含n(n为正整数)
的式子表示上面运算揭示的规律:__________________．
20．如图,正方形ABCD的对角线交于O,OE⊥AB,EF⊥OB,
FG⊥EB．若ΔBGF的面积为1,则正方形ABCD的面积为____________．
三、解答题:
21．计算: 
．
22．先化简再求值: 
,其中m=
, n=
．
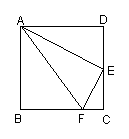
23．如图,正方形ABCD中,E是CD的中点,EF⊥AE．求证:(1)EF平分∠AFC;(2)BF=3FC．
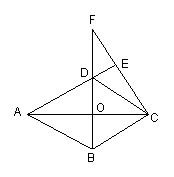
24．如图,菱形ABCD中,CF⊥AD,垂足为E,交BD的延长线于F．求证:AO2=BO•OF．
25．一条河的两岸有一段是平行的．在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆．在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽．
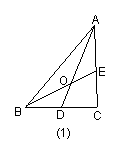
26．在ΔABC中,D为BC的中点,E为AC上的任意一点,BE交AD于点O．某学生在研究这一问题时,发现了如下事实: 如图1,当
时,有
；
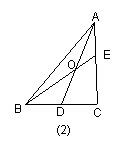
如图2,当
时,有
；
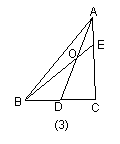
如图3,当
时,有
；在图4中,当
时,
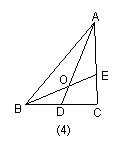
参照上述研究的结论,请你猜想用n表示AO∶AD的一般结论,并给出证明．
答案:
一．
BBACD,ACCDB,CBBC．
二．
15．1<c<5．
16．甲, 
．
17．2
cm．．
18．4∶21．
19．1,1,1, 
20．32．
三．
21．18－
．
22．原式=
．
而
原式=-
．
23．(1)延长FE,AD交于G．
先证ΔDEG≌ΔCEF,得∠G=∠EFC,
而∠G=∠GFA．
(2)先证ΔADE∽ΔECF,
得CF∶CE=DE∶DA=1∶2,
∵CE=ED,CD=CB,
从而CF∶CD=CF∶CB=1∶4．
∴BF=3CF．
24．先证CO=AO,∠FCB=∠FED=900,
又CO⊥BF,
∴CO2=BO·OF．
25．
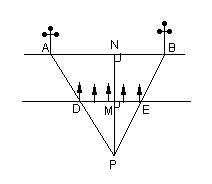
如图,由题知AB=50,DE=20,PM=25;
因DE∥AB,
∴ΔPDE∽ΔPAB,
从而PM∶PN=DE∶AB,
设MN=x米,则25∶(25+x)=20∶50,
x=37．5(米)
26．结论: AE∶AC=1∶(1+n)时,
AO∶AD=2∶(2+n)．
证明:如图4,作DF∥BE,交AC于F．
∵BD=DC,∴EF=FC．
∵AE∶AC=1∶(1+n),∴AE∶EC=1∶n=2∶2n．
∴AE∶EF=2∶n．
∴AO∶AD=AE∶EF=2∶(2+n)．