八年级(下)数学期末综合练习卷
测试时间60分钟 测试分值100分 学生姓名 实际评分
一、选择题(每小题3分，共30分)
1、不等式2x -3≥0的解集是（ ）
A.x≥
B.x＞ C.x＜
D.x≤
2、下列命题中，真命题是（ ）
A. 互补两角若相等，则此两角都是直角 B. 直线是平角
C.
不相交的两条直线叫做平行线
D. 和为
的两个角叫做邻补角
3、已知：如图，AB∥CD，CE平分∠ACD，∠A＝1100，则∠ECD的度数等于
A.110° B.70° C.55° D.35°
4、某学生用一架不等臂天平称药品．第一次将左盘放入50克砝码，右盘放药品使天平平衡．第二次将右盘放入50克砝码，左盘放药品使天平平衡．则两次称得药品的质量和（ ）
A.等于100克 B.大于100克 C.小于100克 D.以上情况都有可能
5、化简：
的结果是（ ）．
A.
B.
C.
D.
6、在△ABC中，I是内心(三角形内角平分线的交点)，∠BIC＝130°，则∠A的度数是（ ）
A.40° B.50° C.65° D.80°
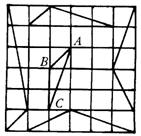
7、如图，△ABC中，DE∥BC，如果AD=1，DB=2，那么
的值为（ ）
A.
B.
C.
D.
 |  | ||
(第3题图) (第7题图) (第8题图)
8、如图，在正方形网格上有五个三角形，其中与△ABC相似(不包括△ABC本身)有( )
A．1个 B．2个 C．3个 D．4个
9、一组数据13，14，15，16，17的标准差是（ ）
A.0 B.10 C.
D.2
10、把一盒苹果分给几个学生，若每人分4个，则剩下3个，若每人分6个，则最后一个学生能得到的苹果不超过2个，则学生人数是( )
A.3 B.4 C.5 D.6
二、填空题(每小题3分，共24分)
11、分解因式：2x2-12x+18= .
12、若a＜b＜0，则1，1-a，1-b这三个数按由小到大的顺序用“＜”连接起来： .
13、计算
的结果是 .
14、在R t△ABC中，锐角A的平分线与锐角B的邻补角的平分线相交于点D，则∠ADB＝____________．
15、北京至石家庄的铁路长392千米，为适应经济发展，自2001年10月21日起，某客运列车的行车速度每小时比原来增加40千米，使得石家庄至北京的行车时间短了1小时。如果设该列车提速前的速度为每小时x千米，那么为求x所列出的方程为______________。
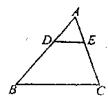
16、如图，在△ABC中，点D在AB上，请再添加一个适当的条件，使△ADC∽△ACB，那么要添加的条件是 。（只需填写满足要求的一个条件即可）。
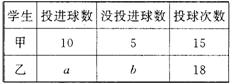17、右表为甲、乙两人比赛投篮球的记录，
以命中率（投进球数与投球次数的比值）来
比较投球成绩的好坏，得知他们的成绩一样
好，下面有四个a，b的关系式：
①a－b＝5 ②a＋b＝18 ③a：b＝2：1 ④a：18＝2：3
其中正确的是
（只填序号）
 |
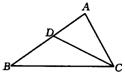(第16题图) (第18题图)
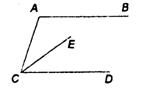
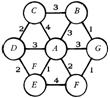
18、某综合性大学拟建校园局域网络，将大学本部A和所属专业学院 B、C、D、E、F、G之间用网线连接起来．经过测算，网线费用如图如示（单位：万元），每个数字表示对应网线（线段）的费用．实际建同时，部分网线可以省略不建，但本部及所属专业学院之间可以传递信息，那么建网所需的最少网线费用为 万元。
三、解答题(每小题6分，共12分)
19、解不等式组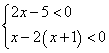
，并把解集在数轴上表示出来。
20、先化简，再求值：
－
，其中x＝
．
四、(每小题8分，共16分)
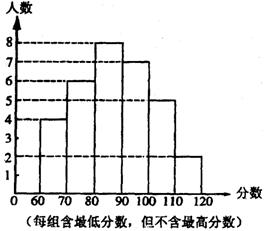
21、某中学部分同学参加全国初中数学竞赛，取得了优异的成绩．指导老师统计了所有参赛同学的成绩（成绩都是整数，试题满分120分），并且绘制了“频数分布直方图”（如图）．
请回答：
(1)中学参加本次数学竞赛的有多少名同学？
(2)如果成绩在90分以上（含90分）的同学获奖，那么该中学参赛同学的获奖率是多少？
(3)这次竟赛成绩的中位数落在哪个分数段内？
(4)图中还提供了其它信息，例如该中学没有获得满分的同学等等．请再写出两条信息．
 |
22、求证：三角形的内角和等于180°(要求画出图形，写出已知、求证和证明过程).
五、(每小题8分，共16分)
23、如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE。
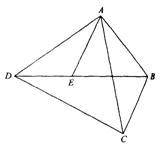求证：△ABE∽△ACD.
24、某工程队要招聘甲、乙两种工种的工人150人，甲、乙两种工种的工人的月工资分别为600元和1000元，现要求乙种工种的人数不少于甲种工种人数的2倍，问甲、乙同种工种各招聘多少人时，可使得每月所付的工资最少？