第九章单元测试
（时间90分钟，满分100分）
一、填空题（每空3分，共42分）
1．已知反比例函数
的图象经过点（2，－3），则k的值是_______,图象在__________象限，当x>0时，y随x的减小而__________.
2.已知变量y与x成反比，当x =1时，y =－6,则当y = 3时，x=________。
3．若反比例函数y=(2m-1)
的图象在第一、三象限,则函数的解析式为___________.
4．已知反比例函数
，当m 时，其图象的两个分支在第一、三象限内；当m 时，其图象在每个象限内
随
的增大而增大；
5.在函数
（
为常数）的图象上有三个点（-2，
），(-1，
)，（
，
），函数值，，的大小为
；
6．已知
是反比例函数
(k≠0)图象上的两点,且
<0时,
,则k________。
7．已知正比例函数y=kx(k≠0),y随x的增大而减小,那么反比例函数y=
,当x< 0时,y随x的增大而_______.
8.已知y1与x成正比例(比例系数为k1),y2与x成反比例(比例系数为k2),若函数y=y1+y2的图象经过点(1,2),(2, 
),则8k1+5k2的值为________.
9. 若m＜－1，则下列函数：①
;② y =－mx+1;
③ y = mx; ④ y =(m + 1)x中，y随x增大而增大的是___________。
10．当＞0,＜0时，反比例函数的图象在__________象限。
11．老师给出一个函数，甲、乙、丙、丁四人各指出这个函数的一个性质，甲：函数图象不经过第三象限；乙：函数图象经过第一象限；丙：随的增大而减小；丁：当
时，
。已知这四人叙述都正确，请构造出满足上述所有性质的一个函数_______________。
二、选择题（每题3分，共24分）
12．若函数的图象过点（3，-7），那么它一定还经过点
（ ）
（A）（3，7） （B）（-3，-7） （C）（-3，7） （D）（2，-7）
13．反比例函数
（m为常数）当
时，随的增大而增大，则
的取值范围是（ ）
A、
B、
C、
D、
14.若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=-
的图象上的点,并且x1<0<x2<x3,则下列各式中正确的是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y1<y3<y2
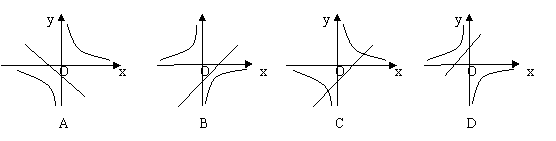
15.如图,已知关于x的函数y=k(x-1)和y=-
(k≠0), 它们在同一坐标系内的图象大致是( )
16.已知力F所做的功是15焦,则力F与物体在力的方向上通过的距
离S的图象大致是如图中的( )
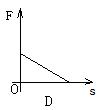
17.如图所示,点P是反比例函数y=图象上一点,过点P分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是 ( )
A.y=-
B. y=
C.y=-
D.y=
18．下面关于反比例函数的意义或性质的综述，正确的是( )
A.自变量x扩大(或缩小)几倍，函数y反而缩小(或扩大)几倍
B.反比例函数是形如y＝(k是常数，k≠0)的函数
C.若x与y的积是一个常数，则y是x的反比例函数
D.当k＞0时，y随x的增大反而减小
19．已知
+
=y,其中与
成反比例,且比例系数为
,而与
成正比例,且比例系数为
,若x=-1时,y=0,则,的关系是( )
A.
=0
B.
=1
C.
=0
D. =-1
三、解答题（共34分）
20．（4分）一定质量的二氧化碳，当它的体积
时，它的密度
.①求
与V的函数关系式；②当
时，求二氧化碳的密度.
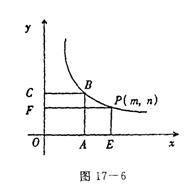
21．（8分）如图所示，已知：正方形OABC的面积为9 ，点O为坐标原点，点A 在x轴上，点C 在y轴上, 点B 在函数
的图象上,点P(m，n)是函数的图象上动点，过点P分别作x
轴、y 轴的垂线，垂足分别为E 、F ，若设矩形OEPF 和正方形OABC不重合的两部分的面积和为S.
(1)求B 点坐标和k 的值；
(2)当
时，求点P的坐标；
(3)写出S 关于m的函数关系式．
.
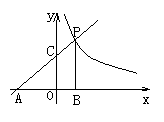
22. （8分）如图,直线y=x+2 分别交x,y轴于点A,C,P是该直线上第一象限内的一点,PB ⊥x轴,B为垂足,
=9.求过P点的坐反比例函数的解析式.
 |
23．（6分）某童装厂现有甲种布料38米，乙种布料26米，现计划用这两种布料生产L、M两种型号的童装共50套.已知做一套L型号的童装需用甲种布料0.5米，乙种布料1米，可获利45元；做一套M型号童装需用甲种布料0.9米，乙种布料0.2米，可获利30元，设生产L型号的童装套数为x，用这批布料生产这两种型号的童装所获的利润为y(元).
(1)写出y(元)关于x(套)的函数解析式，并求出自变量x的取值范围；
(2)该厂在生产这批童装中，当L型号的童装为多少套时，能使该厂所获的利润最大?最大利润为多少?
24. （8分）如图,一次函数的图象与x轴y轴分别交于A,B两点,与反比例的图象交于C, D两点.如果A点的坐标为(2,0),点C,D分别在第一,第三象限,且OA=OB=AC=BD. 试求一次函数和反比例函数的解析式.
 |