华师版八年级第一学期数学期末模拟试题
（满分120，时间90分钟）
一、填空题（每小题2分，共30分）
1、计算：
；
；
2、计算：
；
3、若
是一个多项式的完全平方，则
4、不等式
的负整数解为
5、当
时，不等式
≥
解集为
≤8
6、如图1，已知AC=AD，若使△ABC≌△ABD，请您补充条件 （只需填写一个你认为适当的条件）
7、在平行四边形ABCD中，已知AB=8，周长等于24，则BC=
8、菱形的一条对角线与一条边长相等，这个菱形相邻两个内角的度数分别为
9、如图2，一张宽为6cm的矩形纸片，按图示加以折叠，使得一角顶点落在AB边上，则折痕DF= cm
10、等腰梯形的上底与高相等，下底是上底的3倍，则底角（锐角）等于 度
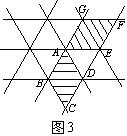11、同学们曾玩过万花筒，它是由三块等宽、等长的玻璃片围成的，如图3是万花筒的一个图案，图中所有三角形均是全等的等边三角形，其中的菱形AEFG可以看成是菱形ABCD以A为中心逆时针旋转
度得到的。
12、某学生第一次数学检测得80分，第二次得86分，那么他第三次检测得分的情况为
时，才能使平均成绩不低于85分。
二、选择题（每小题3分，共30分）
13、下列计算结果是
的是（
）
A、
B、
C、
D、
14、若
，那么
的值是（
）
A、-2 B、-1 C、2 D、3
15、分解因式
结果正确的是（
）
A、
B、
C、
D、
16、若
，
，则
的值为
A、15 B、90 C、100 D、110
17、若当
时，
的值大于零，则
的值只能是（
）
A、0 B、奇数 C、偶数 D、正整数
18、两次翻折（对称轴互相平行）相当于一次（ ）
A、翻折 B、平移 C、旋转 D、中心对称
19、正方形具有而矩形不具有的性质是（ ）
A、对边相等 B、对角线相等
C、对角线互相平分 D、对角线互相垂直
20、如图4所示的图案是我国几家银行标志，其中既是中心对称又是轴对称的有（ ）
A、1个 B、2个 C、3个 D、4个
21、使两个直角三角形全等的条件是（ ）
A、一组锐角对应相等 B、两组锐角分别对应相等
C、一组直角边对应相等 D、两组直角边分别对应相等
22、过矩形的四个顶点分别作对角线的平行线，围成的四边形是（ ）
A、一般四边形 B、矩形 C、菱形 D、正方形
三、计算题（每小题5分，共25分）
23、先化简，再求值。
，其中
，
24、计算
25、解不等式组
26、已知关于的方程
的解是非负数，求
的取值范围。
27、学校有一边长为
的正方形草坪，现将其各边增长
，扩大草坪面积。有同学说“扩建后比扩建前面积增大
”，你认为正确吗？如正确，请说明理由；如不正确，请你计算出扩建后比扩建前草坪面积增大多少？（写出过程）
四、探究题（28题6分，29题9分）
28、如图5，作图说明△A’B’C’是由△ABC通过怎样的图形变换（平移、旋转、轴对称）得到的？
29、已知：如图6，在□ABCD中，E、F分别是BC、AD的中点。
⑴试分析四边形AECF是什么四边形？并证明结论；
⑵当AB⊥AC时，四边形AECF是什么四边形？（不需证明）
⑶结合现有图形，请你添加一个条件，使其与原已知条件共同能推出四边形AECF是矩形。（不可添加AE、CF垂直于BC、AD，不需证明）
 |
五、附加题（展开思维的翅膀，你将飞向成功的彼岸，每题10分，共20分）
30、⑴如图7，已知A、B、C在一条直线上，分别以AB、BC为边在AC同侧作等边三角形ABD和等边三角形BCE，AE交BD于点F，DC交BE于点G。
求证：AE=DC，BF=BG；
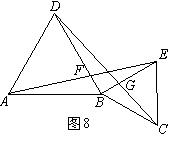
⑵如图8，如果A、B、C不在一条直线上，那么AE=DC和BF=BG是否仍然成立？并请加以说明。
31、某织布厂有200名工人，为改善经营，增设制衣项目，已知每人每天能织布30米，或利用所织布制衣4件，制衣一件用布1.5米，将布直接出售，每米可获利2元；将布制成衣出售，每件可获利25元，若每名工人一天只能做一项工作，且不计其他因素，设一天安排名工人制衣，则
⑴一天中制衣所获利润P=
元（用含的代数式表示）；
⑵一天中剩余布所获利润Q=
元（用含的代数式表示）；
⑶当取何值时，该厂一天中所获利润W（元）最大？最大利润是多少？
参考答案
1、
；
；
2、
；
3、1 4、-2，-1
5、≤0 6、∠CAB=∠DAB 7、4 8、60°，120° 9、8 10、45 11、120
12、不低于89分 13、C 14、C 15、D 16、D 17、B 18、B 19、D
20、B 21、D 22、C 23、
，-1 24、-3 25、
26、≥-3
27、不正确，扩建后比扩建前草坪面积增大
28、先将△ABC以B点为中心，沿逆时针方向旋转90°，再将得到的图形向右平移两个单位即得△A’B’C’
29、⑴四边形AECF是平行四边形，证明略
⑵四边形AECF是菱形
⑶AB=AC
30、⑴提示：通过证明△ABE≌△DBC得出AE=DC；
通过证明△BFE≌△BGC得出BF=BG
⑵AE=DC仍然成立，但BF=BG不成立，证明略
31、⑴100
⑵12000
⑶当
166时，所获利润W最大，最大利润为16600元