实数的有关概念自我测试
[复习要点]
（1）______和______统称为有理数._______________叫做无理数.有理数和无理数统称______.
（2）规定了_____、_____和单位长度的直线叫做数轴.实数与数轴上的点_______.
（3）只有______不同的两个实数，叫做互为相反数，零的相反数是______；实数a与b互为相反数
（4）1除以一个__________的数的商叫做这个数的倒数._________没有倒数；实数a与b互为倒数
（5）数轴上表示数a的点与_____的距离叫做a的绝对值，记作______.正数和零的绝对值是它_______，负数的绝对值是它的_______.若a=a，则a____0；若a=-a，则a_____0；若a<0，则a=________.
（6）将一个数四舍五入所得到的数，叫做这个数的__________.四舍五入到哪一位，就说这个近似数精确到哪一位，这时从左边第一个不是______的数字起，到精确到的_______止，所有的数字都叫做这个近似数的有效数字.
（7）把一个大于0的数记成a×10n的形式，其中n是整数，1≤a<10，这种记数法叫做______________.
（8）实数的大小比较.在数轴上表示的两个数，右边的点所表示的实数总比左边的点所表示的实数_____.正数大于______和一切_____；零大于一切_______；两个正数，绝对值大的较_____；两个负数，绝对值大的反而______.
[基础训练]
1、选择题
（1）在实数
…中，无理数有（ ）
A、4个 B、5个 C、6个 D、7个
（2）下列各组数中，互为相反数的是（ ）
A、2与0.5 B、（-1）2与1 C、-1与（-1）2 D、2与-1
（3）如图，在数轴上表示1，
的对应点分别为A、B.点B关于点A的对称点为C，则点C所表示的数是（ ）
A、-1 B、1- C、2- D、-2
3、填空题
（1）用科学计数法表示：=__________，0.000702=__________.
（2）近似数0.30精确到_____位，有_____个有效数字.
（3）绝对值小于4的整数是_____________；绝对值小于4的非负整数是_________.
（4）设a是大于1的实数，若
在数轴上的对应点分别为A、B、C，则A、B、C三点在数轴上自左至右的顺序是_______________.
（5）观察下列算式：31=3，32=9，33=27，34=81，35=243，36=729，37=2187，38=6561……用你发现的规律写出32003的末位数字是___________，
[典型例题]
例1：若实数a、b在数轴上的位置如图所示，试化简：
 |
例2：比较下列各组数的大小.
（1）
例3：已知a、b互为相反数，c、d互为倒数，e是非零实数，求
的值.
例4：已知一列数1，-2，3，-4，5，-6，7，……将这列数排成下列形式：
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
……
按照上述规律排下去，那么第10行从左边数第5个数等于（ ）
A、50 B、-50 C、60 D、-60
例5：人的身高很大程度上由遗传决定，从父母的身高一定程度上可以预测子女成年后能达到的身高.科学家经研究得出了人的身高与父母身高的一组相关数据，如下表所示.
| 父亲身高a/m | 母亲身高b/m | 儿子身高y/m | 女儿身高t/m |
| 1.68 | 1.58 | （1.68+1.58）×0.54 | 1.68×0.52+1.58×0.4615 |
| 1.72 | 1.62 | （1.72+1.62）×0.54 | 1.72×0.52+1.62×0.4615 |
| 1.76 | 1.66 | （1.76+1.66）×0.54 | 1.76×0.52+1.66×0.4615 |
| 1.80 | 1.70 | （1.80+1.70）×0.54 | 1.80×0.52+1.70×0.4615 |
| …… | …… | …… | …… |
（1）请你根据表中提供的信息，得出人的遗传基因长高公式；
（2）初三年级男生李明的父亲身高175cm，母亲身高160cm，试预测李明成年后的身高.
[巩固练习]
1、选择题
（1）如果a与-2互为倒数，那么a是（ ）
A、-2 B、-0.5 C、0.5 D、2
（2）实数m、n在数轴上的位置如图所示，则下列不等关系正确的是（ ）
A、n<m B、n2<m2
C、n0<m0 D、n<m
（3）若a-3-3+a=0，则a的取值范围是（ ）
A、a≤3 B、a<3 C、a≥3 D、a>3
（4）冬季某天我国三个城市的最高气温分别是-10℃，1℃，-7℃，把它们按从高到低的顺序排列，正确的是（ ）
A、-10℃，-7℃，1℃ B、-7℃，-10℃，1℃
C、1℃，-7℃，-10℃ D、1℃，-10℃，-7℃
（5）下列关于
的说法中，错误的是（ ）
A、是无理数 B、3<<4
C、是12的一个平方根 D、是最简二次根式
（6）北京等5个城市的国际标准时间（单位：h）可在数轴上表示如下：
如果将两地国际标准时间的差简称为时差，那么（ ）
A、汉城与纽约的时差为13h B、汉城与多伦多的时差为13h
C、北京与纽约的时差为14h D、北京与多伦多的时差为14h
（7）一批货物总重1.4×107kg，下列可将其一次性运走的合适运输工具是（ ）
A、一艘万吨级巨轮 B、一架飞机 C、一辆汽车 D、一辆板车
（8）如图，如果数轴上的点E和点F表示的数相乘，那么图中表示最接近于这个积的点是（ ）
A、M B、P C、Q D、N
（9）在一列数1，2，3，4，……，1000中，数字“0”出现的次数共是（ ）
A、182 B、189 C、192 D、194
（10）“数轴上的点并不都表示有理数，如图中数轴上的点P所表示的数是”，这种说明问题的方式体现的数学思想方法叫做（ ）
A、代入法 B、换元法
C、数形结合 D、分类讨论
2、填空题
（1）当a=________时，它没有倒数；当a=______时，它的倒数是本身；
（2）数轴上与原点距离为5的点所表示的数是___________；
（3）2.1794精确到百分位的近似值是____；279600保留三个有效数字的近似数是___.
（4）已知无理数a满足不等式1<a<4，请写出两个你熟悉的无理数a=______，______..
（5）某市召集20名特级教师参加教改研讨会，与会的特级教师每两个人之间都要握手一次，那么他们之间一共握手________次.
（6）已知a=5，
，且ab>0，则a+b=_____
（7）如图，在数轴上点A和点B之间表示整数的点有___个.
（8）一跳蚤在一直线上从O点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……依此规律跳下去，当它跳第100次落下时，落点处离O点的距离是__________个单位.
（9）现有四个有理数3，4，-6，10，将这四个数（每个数用且只用一次）进行加减乘除四则运算，使其结果等于24，请你写出一个符合条件的算式____________________.
（10）判断一个整数能否被7整除，只需看去掉一节尾（这个数的末位数字）后所得到的数与此一节尾的5倍的和能否被7整除.如果这个和能被7整除，则原数就能被7整除.如126，去掉6后得12，12+6×5=42，42能被7整除，则126能被7整除.类似地，还可通过看去掉该数的一节尾后与此一节尾的n倍的差能否被7整除来判断，则n=______（n是整数，且1≤n<7）.
（11）瑞士中学教师巴尔末成功地从光谱数据
，……中，得到巴尔末公式，从而打开了光谱奥妙的大门.请你按这种规律写出第七个数据是___________.
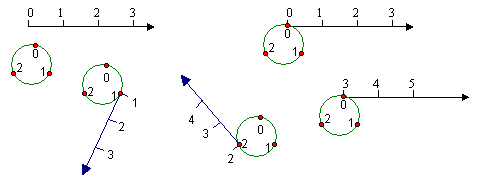
（12）如图所示，按下列方法将数轴的正半轴绕在一个圆（该圆周长为3个单位长，且在圆周的三等分点处分别标上了数字0、1、2）上，先让原点与圆周上的0所对应的点重合，再将正半轴按顺时针方向绕在该圆周上，使数轴上1、2、3、4……所对应的点分别与圆周上1、2、0、1……所对应的点重合.这样，正半轴上的整数就与圆周上的数字建立了一种对应关系.
（1）圆周上的数字a与数轴上的数5对应，则a=____________；
（2）数轴上的一个整数点刚刚绕过圆周n圈（n为正整数）后，并落在圆周上数字1所对应的位置，这个整数是____________（用含n的代数式表示）.
 |