南开区2005年九年级数学升学检测试卷(一)
一. 选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. ![]() 中
中![]() ,
,![]() 与
与![]() 度数之比为
度数之比为![]() ,则
,则![]() (
)
(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
1
D.
1
2. 若分式![]() 对于无论
对于无论![]() 取何实数总有意义,则
取何实数总有意义,则![]() 的取值范围是(
)
的取值范围是(
)
A. ![]() B.
B. ![]() C.
C. ![]() 且
且![]() D.
D. ![]()
3. 甲、乙二人分别从A、B两地同时出发,相向而行,在C地相遇后,甲又经过![]() 小时到达B地,乙又经过
小时到达B地,乙又经过![]() 小时到达A地,设AC=S1,BC=S2,那么
小时到达A地,设AC=S1,BC=S2,那么![]() 等于(
)
等于(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 一组数据为:1,2,8,4,3,9,5,4,5,4,现有如下判断:
① 这组数据的中位数是6
② 这组数据的众数是4
③ 这组数据的平均数是4
④ 以这组数据为样本,其样本容量是9
其中正确的判断个数是()
A. 1个 B. 2个 C. 3个 D. 4个
5. 若![]() 的三边长分别为
的三边长分别为![]() 、
、![]() 、
、![]() ,且满足
,且满足![]() ,则
,则![]() 一定是(
)
一定是(
)
A. 直角三角形 B. 等边三角形
C. 等腰三角形 D. 等腰直角三角形
6. 若平行四边形的四个内角的平分线能围成一个四边形,则这个四边形一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
7. 现给出以下命题:
① 两圆相交,公共弦所在的直线必平分外公切线的长。
② 两圆外切,内公切线被两条外公切线所截得的线段长等于外公切线的长。
③ 两圆外离,外公切线的长必大于内公切线的长。
④ 两圆同心,从大圆上任一点引小圆的切线,所有的切线长都相等。
其中错误命题的个数为()
A. 3个 B. 2个 C. 1个 D. 0个
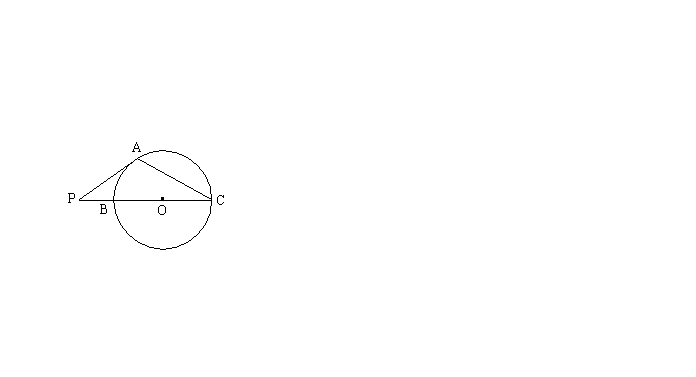
8. 如图,PA为⊙O的切线,A为切点,割线PBC过圆心O,![]() ,OC=1cm,则PA的长为( )
,OC=1cm,则PA的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9. 正六边形的周长为12,则它的外接圆的内接正三角形的周长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
6
D.
6
10. 抛物线![]() 开口向下,与
开口向下,与![]() 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为![]() 和3,现给出如下判断:
和3,现给出如下判断:
① ![]() ②
②
![]() ③
③
![]() ④
④
![]()
⑤ ![]() ⑥
⑥
![]() ⑦
⑦
![]() ⑧
⑧
![]()
其中正确判断的个数为()
A. 2个 B. 3个 C. 4个 D. 5个
二. 填空题:本题共8小题,每小题3分,共24分,请将答案直接填在题中横线上。
11. 关于![]() 的方程
的方程![]() 的一个实数根的倒数恰是它本身,则
的一个实数根的倒数恰是它本身,则![]() 的值为
。
的值为
。
12. 正比例函数![]() 与反比例函数
与反比例函数![]() 两个交点间的距离为
。
两个交点间的距离为
。
13. ![]() 中
中![]() ,斜边AB的中线长为3,
,斜边AB的中线长为3,![]() ,则
,则![]() 。
。
14. 直角梯形的一条对角线将它分成两个三角形,其中一个是等边三角形,如果梯形的中位线长为![]() ,那么这个梯形的下底长为
。
,那么这个梯形的下底长为
。
15. 在![]() 中,
中,![]() ,过AC上一点D作直线DE,交AB于E,使
,过AC上一点D作直线DE,交AB于E,使![]() 和
和![]() 相似,这样的直线可作
条。
相似,这样的直线可作
条。
16. 两圆半径分别为R、r,一条外公切线长恰为![]() ,则这两圆的位置关系是
。
,则这两圆的位置关系是
。
17. 直角三角形的外接圆半径为5,内切圆半径为2,则此三角形周长为 。
18. 如图,在边长为![]() 的菱形ABCD中,
的菱形ABCD中,![]() ,E是AD上不同于A、D两点的一动点,F是CD上一动点,且AE+CF=
,E是AD上不同于A、D两点的一动点,F是CD上一动点,且AE+CF=![]() ,则
,则![]() 面积的最小值为
。
面积的最小值为
。
三. 解答题:本大题共8个小题,其中第19题6分,第20�24题每题8分,第25�26题每题10分,共66分,解答应写出文字说明,演算过程或证明过程。
19.(本小题6分)
两台机床同时生产直径为10的零件,为了检验产品质量,质量检验是从两台机床的产品中各抽出4件进行测量,结果如下:
| 机床甲 | 10 | 9.8 | 10 | 10.2 |
| 机床乙 | 10.1 | 10 | 9.9 | 10 |
请你分析哪一台机床生产的零件质量更符合要求。
20.(本小题8分)
解方程:![]()
21.(本小题8分)
如图,一次函数![]() 的图象经过B、C,A是此图象上一点,AM垂直于
的图象经过B、C,A是此图象上一点,AM垂直于![]() 轴,垂足为M,求:
轴,垂足为M,求:
(1)一次函数![]() 的解析式;
的解析式;
(2)梯形ABOM的面积S;
(3)![]() 的正弦函数的值。
的正弦函数的值。

22.(本小题8分)
已知二次函数![]() 中,当
中,当![]() 时,
时,![]() 有最大值4,二次函数图象与
有最大值4,二次函数图象与![]() 轴两个交点的横坐标分别为
轴两个交点的横坐标分别为![]() 、
、![]() ,且
,且![]() ,求此抛物线的解析式。
,求此抛物线的解析式。
23.(本小题8分)
如图,某水库大坝的横断面是一梯形ABCD,坝顶宽CD=3米,斜坡AD=16米,坝高8米,斜坡BC的坡度![]() ,求:
,求:
(1)斜坡AD的坡度;
(2)坝底宽AB的长(结果保留根号)

24.(本小题8分)
已知:如图,⊙O1与⊙O2相交于A、B两点,且O2在⊙O1上,P为⊙O1上一点,PC、PD为⊙O2的切线,C、D为切点,PC交⊙O1于E,PD的延长线交⊙O1于F,求证:AB∥EF。

25.(本小题10分)
已知![]() 是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过点P作BC的平行线交直线BT于点E,交直线AC于点F。
是⊙O的内接三角形,BT为⊙O的切线,B为切点,P为直线AB上一点,过点P作BC的平行线交直线BT于点E,交直线AC于点F。
(1)如图,当点P在线段AB上时,求证:![]()
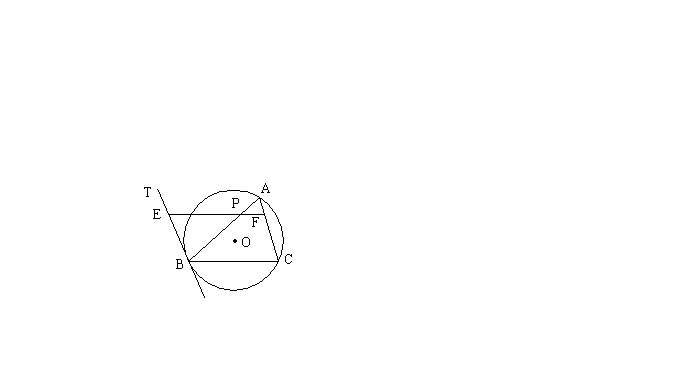
(2)如图,当点P是线段BA延长线上一点时,试问![]() 是否成立,并证明你的结论。
是否成立,并证明你的结论。

26.(本小题10分)
已知过点M(1,4)的抛物线![]() 与直线
与直线![]() 相交于A、P两点,与
相交于A、P两点,与![]() 轴相交于点Q,点E是线段PQ的中点,点A在
轴相交于点Q,点E是线段PQ的中点,点A在![]() 轴的负半轴上,且OA的长为
轴的负半轴上,且OA的长为![]() 。
。
(1)求直线和抛物线的解析式;
(2)求![]() 的外接圆的直径;
的外接圆的直径;
(3)若点B(![]() ,
,![]() )在
)在![]() 的外接圆上,直线QM与直线EB相交于点T,求
的外接圆上,直线QM与直线EB相交于点T,求![]() 的度数。
的度数。
南开区2005年九年级数学升学检测试卷
参考答案
一. 选择题(每小题3分,共30分)
1. A 2. B 3. D 4. A 5. C 6. A 7. D 8. B 9. C 10. B
二. 填空题(每小题3分,共24分)
11. 2或![]() 12.
12.
![]() 13.
13.
![]() 14.
14.
![]() 15.
2 16. 外离或外切
15.
2 16. 外离或外切
17. 24 18. ![]()
三. 解答题(共66分)
19. ![]() (1分)
(1分)
![]() (2分)
(2分)
∴ ![]() (3分)
(3分)
![]()
![]() (4分)
(4分)
![]() (5分)
(5分)
∴ ![]() (5分)
(5分)
故机床乙生产的零件质量更符合要求(6分)
20. ![]()
设![]() ,原方程化为
,原方程化为![]() (2分)
(2分)
化为整式方程![]()
解得![]()
![]() (3分)
(3分)
当![]() 即
即![]()
![]() 有
有![]()
解得![]() ,
,![]() (5分)
(5分)
当![]() 即
即![]() 有
有![]()
此方程![]() 无解(7分)
无解(7分)
经检验,原方程的解为![]() ,
,![]() (8分)
(8分)
21.
(1)由图象B(0,2),C(![]() ,0),M(4,0)
,0),M(4,0)
∴ ![]() 解得
解得![]()
∴ 一次函数解析式为![]() (3分)
(3分)
(2)由题设点A的横坐标为4
∴ 纵坐标![]() (4分)
(4分)
![]()
![]() (6分)
(6分)
(3)AM∥![]() 轴
∴
轴
∴ ![]()
![]() 中OC=3,OB=2
中OC=3,OB=2
由勾股定理![]()
∴ ![]() (8分)
(8分)
22. ![]()
![]() ,
,![]() (4分)
(4分)
![]()
![]() (6分)
(6分)
依题意![]() 解得
解得![]() (7分)
(7分)
∴ 抛物线的解析式为![]() (8分)
(8分)
23.
(1)作DE⊥AB于E
![]() 中,
中,![]() (2分)
(2分)
∴ ![]() (3分)
(3分)
∴ 斜坡AD的坡度为![]() (4分)
(4分)
(2)作CF⊥AB于F,则CF=DE=8(5分)
![]() ∴
∴ ![]() (6分)
(6分)
又EF=CD=3AE=![]() (7分)
(7分)
∴ AB=AE+EF+BF=![]() (8分)
(8分)
24. 连PO2、O1O2
∵ ⊙O1与⊙O2相交于A、B两点
∴ AB⊥O1O2
PC、PD分别切⊙O2于C、D
由切线长定理![]() (4分)
(4分)
即![]()
∵ ![]() 在⊙
在⊙![]() 上
∴
上
∴ ![]() (5分)
(5分)
⊙![]() 中由垂径定理EF⊥O1O2(7分)
中由垂径定理EF⊥O1O2(7分)
由AB⊥O1O2,EF⊥O1O2
∴ AB∥EF(8分)
25.
(1)BT切⊙O于B
∴ ![]() (1分)
(1分)
即![]() ∵ EF∥BC ∴
∵ EF∥BC ∴ ![]() (2分)
(2分)
∴ ![]() (3分)
(3分)
![]() 和
和![]() 中,
中,![]()
![]()
∴ ![]() 中(4分)
中(4分)
∴ ![]()
故![]() (5分)
(5分)
(2)仍然成立(6分)
∵ BT切⊙O于B ∴ ![]()
即![]() (7分)
(7分)
∵ EF∥BC ∴
![]()
∴ ![]() (8分)
(8分)
![]() 和
和![]() 中,
中,![]() ,
,![]() 是公共角
是公共角
∴ ![]() (9分) ∴
(9分) ∴ ![]()
故![]() (10分)
(10分)
26.
(1)∵ A在![]() 轴的负半轴上
轴的负半轴上
![]()
∴ ![]() (
(![]() ,0)
,0)
它在直线![]() 上,∴
上,∴
![]()
解得![]() ∴ A(
∴ A(![]() ,0)(1分)
,0)(1分)
直线的解析式为![]() (2分)
(2分)
∵ M(1,4)、A(![]() ,0)在抛物线
,0)在抛物线
∴ 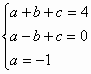
解得![]() ,
,![]() ,
,![]()
∴ 抛物线的解析式为![]() (4分)
(4分)
(2)抛物线![]() 与
与![]() 轴交于Q(0,3)(5分)
轴交于Q(0,3)(5分)
由
解得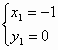
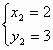
∴ P(2,3)(6分)
![]()
顶点为(1,4)即M为抛物线顶点(7分)
由Q(0,3)、P(2,3)得PQ∥![]() 轴
轴
E是PQ中点 ∴ E(1,3)
且![]() ∴
∴
![]() 是等腰三角形
是等腰三角形
又![]()
∴ ![]() 是等腰直角三角形
是等腰直角三角形
其外接圆直径为PQ=2(8分)
(3)作直线![]() ,交⊙E于B,交PQ于C
,交⊙E于B,交PQ于C
① 如图,当B在PQ上方时,由![]()
可知![]() 又
又
![]() ∴
∴
![]() (9分)
(9分)
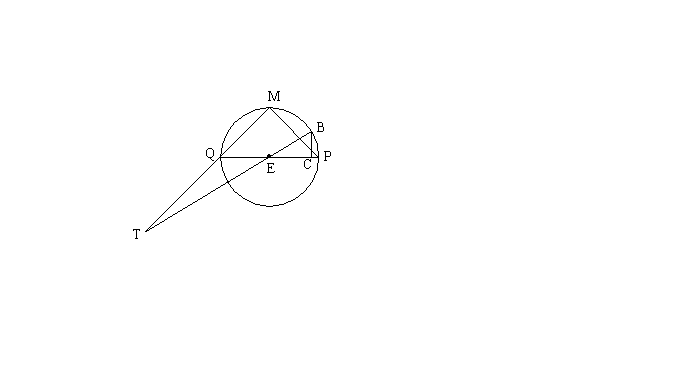
② 如图当B在PQ下方时
![]() (10分)
(10分)
