重庆市2004年普通高中招生统一考试
数 学 试 卷
(本卷共四大题,满分150分,考试时间120分钟)
一、选择题:(本大题12个小题,每小题4分,共48分)每小题只有一个答案是正确的,请将正确答案的代号填入题后的括号内。
1、计算2-(-3)的结果为( )
A、-5 B、5 C、1 D、-1
2、若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是( )
的取值范围是( )
A、![]() >
>![]() B、
B、![]() <
<![]() C、
C、![]() >
>![]() D、
D、![]() <
<![]()
3、化简![]() 的结果为( )
的结果为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、若分式![]() 的值为零,则
的值为零,则![]() 的值为( )
的值为( )
A、3 B、3或-3
C、-3 D、0
5、如图,在菱形ABCD中,∠BAD=800,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
A、800 B、700 C、650 D、600
6、某班七个合作学习小组人数如下:5、5、6、![]() 、7、7、8。已知这组数据的平均数是6,则这组数据的中位数是( )
、7、7、8。已知这组数据的平均数是6,则这组数据的中位数是( )
A、7 B、6 C、5.5 D、5
7、已知任意四边形ABCD中,对角线AC、BD交于点O,且AB=CD,若只增加下列条件中的一个:①AO=BO;②AC=BD;③![]() ;④∠OAD=OBC,一定能使∠BAC=∠CDB成立的可选条件是( )
;④∠OAD=OBC,一定能使∠BAC=∠CDB成立的可选条件是( )
A、② ④ B、① ② C、③ ④ D、② ③ ④
8、二次函数![]() 的图象如图,则点M(
的图象如图,则点M(![]() ,
,![]() )在( )
)在( )

A、第一象限 B、第二象限 C、第三象限 D、第四象限
9、如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为![]() (入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan
(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tan![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、秋千拉绳长3米,静止时踩板离地面0.5米,某小朋友荡该秋千时,秋千在最高处踩板离地面2米(左右对称),则该秋千所荡过的圆弧长为( )
A、![]() 米
B、
米
B、![]() 米
C、
米
C、![]() 米
D、
米
D、![]() 米
米
11、在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B是方格纸中的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点C使△ABC的面积为2个平方单位,则满足条件的格点C的个数是( )
A、5 B、4
C、3 D、2
12、如图,△ABC是等腰直角三角形,AC=BC=![]() ,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )
,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题:(本大题8个小题,每小题4分,共32分)请将答案直接填写在题后的横线上。
13、化简:![]() =
。
=
。
14、如果关于![]() 的不等式
的不等式![]() 和
和![]() 的解集相同,则
的解集相同,则![]() 的值为 。
的值为 。
15、已知反比例函数![]() 与一次函数
与一次函数![]() 的图象的一个交点的纵坐标是-4,则
的图象的一个交点的纵坐标是-4,则![]() 的值是 。
的值是 。
16、如图,ABCD是面积为![]() 的任意四边形,顺次连结各边中点得到四边形
的任意四边形,顺次连结各边中点得到四边形![]() ,再顺次连结
,再顺次连结![]() 各边中点得到四边形
各边中点得到四边形![]() ,重复同样的方法直到得到四边形
,重复同样的方法直到得到四边形![]() ,则四边形
,则四边形![]() 的面积为 。
的面积为 。

17、某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个半径为5cm 的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示),则钢管的内直径AD长为 cm。

18、如图,在△ABC中,∠ACB=900,AC=![]() ,斜边AB在
,斜边AB在![]() 轴上,点C在
轴上,点C在![]() 轴的正半轴上,点A的坐标为(2,0)。则直角边BC所在直线的解析式为
。
轴的正半轴上,点A的坐标为(2,0)。则直角边BC所在直线的解析式为
。

19、如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则该平行四边形的面积是
。

20、某书城开展学生优惠售书活动,凡一次性购书不超过200元的一律九折优惠,超过200元的,其中200元按九折算,超过200元的部分按八折算。某学生第一次去购书付款72元,第二次又去购书享受了八折优惠,他查看了所买书的定价,发现两次共节省了34元钱。则该学生第二次购书实际付款 元。
三、解答题:(本大题4个小题,共46分)下列各题解答时必须给出必要的演算过程或推理步骤。
21、(10分)已知关于![]() 的一元二次方程
的一元二次方程![]() 的两个不相等的实数根α、β满足
的两个不相等的实数根α、β满足![]() ,求
,求![]() 的值。
的值。
22、(12分)每年6月5日是“世界环境日”,保护地球生态环境是世界各国政府和人民应尽的义务。下表是我国近几年来废气污染排放量统计表,请认真阅读该表后,解答题后的问题。
| 年度 | 二氧化硫排放量 | 烟尘排放量 | 工业粉尘排放量 | ||||
| 总量 | 其中 | 总量 | 其中 | ||||
| 工业 | 生活 | 工业 | 生活 | ||||
| 1998 | 2091.4 | 1594.4 | 497.0 | 1455.1 | 1178.5 | 276.6 | 1321.2 |
| 1999 | 1857.5 | 1460.1 | 397.4 | 1159.0 | 953.4 | 205.6 | 1175.3 |
| 2000 | 1995.1 | 1612.5 | 382.6 | 1165.4 | 953.3 | 212.1 | 1092 |
| 2001 | 1947.8 | 1566.6 | 381.2 | 1069.8 | 851.9 | 217.9 | 990.6 |
| 2002 | 1926.6 | 1562.0 | 364.6 | 1012.7 | 804.2 | 208.5 | 941.0 |
(1)请你用不同的虚、实、粗线分别画出二氧化硫排放总量、烟尘排放总量和工业粉尘排放量的折线走势图;

(2)2002年相对于1998年,全国二氧化硫排放总量、烟尘排放总量和工业粉尘排放量的增长率分别为 、 、 。(精确到1个百分点)
(3)简要评价这三种废气污染物排放量的走势。(要求简要说明:总趋势,增减的相对快慢)
23、(12分)某出租汽车公司有出租车100辆,平均每天每车消耗的汽油费为80元,为了减少环境污染,市场推出一种叫“CNG”的改烧汽油为天然汽的装置,每辆车改装价格为4000元。公司第一次改装了部分车辆后核算:已改装后的车辆每天的燃料费占剩下末改装车辆每天燃料费用的![]() ,公司第二次再改装同样多的车辆后,所有改装后的车辆每天的燃料费占剩下末改装车辆每天燃料费用的
,公司第二次再改装同样多的车辆后,所有改装后的车辆每天的燃料费占剩下末改装车辆每天燃料费用的![]() 。问:
。问:
(1)公司共改装了多少辆出租车?改装后的每辆出租车平均每天的燃料费比改装前的燃料费下降了百分之多少?
(2)若公司一次性将全部出租车改装,多少天后就可以从节省的燃料费中收回成本?
24、(12分)如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P。
(1)求证:![]()
(2)若⊙O的直径为25,AB=20,AD=15,求PC和DC的长。

四、解答题:(本大题2个小题,共24分)下列各题解答时必须给出必要的演算过程或推理步骤。
25、(12分)如图,AB、CD是两个过江电缆的铁塔,塔AB高40米,AB的中点为P,塔底B距江面的垂直高度为6米。跨江电缆因重力自然下垂近似成抛物线形,为了保证过往船只的安全,电缆下垂的最低点距江面的高度不得少于30米。已知:人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上;再向西前进150米后从地面F点恰好看到点F、A、C在一直线上。
(1)求两铁塔轴线间的距离(即直线AB、CD间的距离);
(2)若以点A为坐标原点,向东的水平方向为![]() 轴,取单位长度为1米,BA的延长方向为
轴,取单位长度为1米,BA的延长方向为![]() 轴建立坐标系。求刚好满足最低高度要求的这个抛物线的解析式。
轴建立坐标系。求刚好满足最低高度要求的这个抛物线的解析式。


26、(12分)如图,在直角坐标系中,正方形ABOD的边长为a,O为原点,点B在![]() 轴的负半轴上,点D在y轴的正半轴上,直线OE的解析式为y=2x,直线CF过x轴上的一点C(
轴的负半轴上,点D在y轴的正半轴上,直线OE的解析式为y=2x,直线CF过x轴上的一点C(![]() ,0)且与OE平行,现正方形以每秒
,0)且与OE平行,现正方形以每秒![]() 的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为
的速度匀速沿x轴正方向平行移动,设运动时间为t秒,正方形被夹在直线OE和CF间的部分的面积为![]() 。
。
(1)当0≤t<4时,写出![]() 与
与![]() 的函数关系式。
的函数关系式。
(2)当4≤t≤5时,写出S与t的函数关系式,在这个范围内S有无最大值?若有,请求出最大值,若没有请说明理由。


重庆市2004年普通高中招生统一考试
数学试题参考答案与评分意见
一、选择题:
1、B 2、C 3、A 4、C 5、D 6、B
7、A 8、D 9、D 10、B 11、A 12、B
二、填空题:
13、6a2b-1; 14、7; 15、-8; 1 6、![]() ;
;
17、18; 18、![]() ; 19、72; 20、204
; 19、72; 20、204
三、解答题:
21、解;由判别式大于零,得
![]() …………………………………………………(1分)
…………………………………………………(1分)
解得:![]() <
<![]() ……………………………………………………………(3分)
……………………………………………………………(3分)
∵![]() 即
即![]() ,∴
,∴![]() …………………………(4分)
…………………………(4分)
又![]()
![]() ……………………………………(6分)
……………………………………(6分)
代入上式得![]() ,解之
,解之![]() ,
,![]() ……………………(8分)
……………………(8分)
∵![]() >
>![]() ,故舍去……………………………………………………(9分)
,故舍去……………………………………………………(9分)
∴![]() ………………………………………………………………(10分)
………………………………………………………………(10分)
22、(1)正确画图………………………………………………………………(6分)

(2)-8%,-30%,-29%…………………………………………………(9分)
(3)评价:总体均成下降趋势……………………………………………………(10分 )
二氧化硫排放量下降趋势最小…………………………………………(11分)
烟尘排放量趋势最大……………………………………………………(12分)
23、解;(1)设公司第一次改装了![]() 辆车,改装后的每辆出租车每天的燃料费比改装前的燃料费下降的百分数为
辆车,改装后的每辆出租车每天的燃料费比改装前的燃料费下降的百分数为![]() 。……………………………………………………(1分)
。……………………………………………………(1分)
依题意得方程组: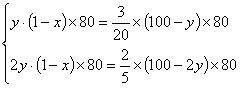 …………………(4分)
…………………(4分)
化简得:![]() ……………………………………(6分)
……………………………………(6分)
解得: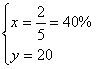 …………………………………………………………(8分)
…………………………………………………………(8分)
答;公司共改装了40辆车,改装后的每辆出租车每天的燃料费比改装前的燃料费下降了40%。
(2)设一次性改装后,![]() 天可以收回成本,则:
天可以收回成本,则:
100×80×40%×![]() =4000×100………………………………………(10分)
=4000×100………………………………………(10分)
解得:![]() =125(天)………………………………………………(12分)
=125(天)………………………………………………(12分)
答:125天后就可以从节省的燃料费中收回成本。
24、证明:
(1)∵∠ADC+∠B=180°,∠B=∠ACB
∴∠ACP+∠ACB=∠ACP+∠B=180°
∴∠ADC=∠ACP……………………………………………………………(2分)
∴△ADC∽△ACP……………………………………………………………(3分)
∴![]() ,即
,即![]() …………………………………………(4分)
…………………………………………(4分)
(2)过点A作直径AE交BC于点F。
∵△ABC是等腰三角形
∴AE垂直平分BC……………………………………(5分)
设AF=![]() ,则EF=
,则EF=![]() ,
,![]()
由BF2=AF·EF,得![]()
所以AF=![]() =16,BF=FC=12………………………………………………(7分)
=16,BF=FC=12………………………………………………(7分)
方法1:
由(1)AB2=AD·AP得:![]() ……………………(8分)
……………………(8分)
在Rt△AFP中,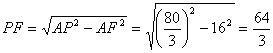 …………(9分)
…………(9分)
∴PC=PF-FC=![]() =
=![]() ……………………………………………(10分)
……………………………………………(10分)
又由△PCD∽△PAB得:![]()
∴![]() …………………………………………(12分)
…………………………………………(12分)


方法2:(前面部分给分相同)连接BE、EC、BD
∵AE是直径
∴∠ABE=900,且BE=![]()
∴EC=BE=15,又已知AD=15,∴AD=EC……………………………(8分)
∴DC∥AE,即DC⊥BC,则BD是直径…………………………………(9分)
∴DC=![]() ………………………………(10分)
………………………………(10分)
在Rt△PCD中,PD=PA-AD=![]() =
=![]()
∴PC=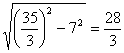 …………………………………………………(12分)
…………………………………………………(12分)
四、解答题:
25、解:如图,AB=40米,BP=20米,BE=50米,BF=50+150=200(米)。
设CD的延长线交地平面于点H。
(1)设CH=![]() ,BH=
,BH=![]() …………………………………………………(1分)
…………………………………………………(1分)
由△EBP∽△EHC得![]() ,即
,即![]() ………①………(2分)
………①………(2分)
由△FBA∽△FHC得![]() ,即
,即![]() ……②………(3分)
……②………(3分)
由①②解得:![]() ,
,![]()
答:两铁塔轴线间的距离为100米。…………………………………(5分)

(2)依题意建立坐标系如图,由(1)得CH=60米,C点比A点高20米,这时A、C两点的坐标为:A(0,0),C(100,20),设抛物线顶点为P(![]() ,
,![]() ),因为要求最低点高于地面为30-6=24(米),点A高度为40米,所以
),因为要求最低点高于地面为30-6=24(米),点A高度为40米,所以![]() =-16。设过点A的抛物线解析式为
=-16。设过点A的抛物线解析式为![]() (
(![]() >0),则该抛物线满足:…………………………(6分)
>0),则该抛物线满足:…………………………(6分)
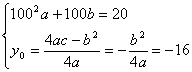 ………………………………………………(8分)
………………………………………………(8分)
化简得:![]()
解得:![]() ,
,![]() …………………………………………………(9分)
…………………………………………………(9分)
∵抛物线的对称轴在![]() 轴的右侧,有
轴的右侧,有![]() >0,而
>0,而![]() >0
>0
∴![]() <0,故
<0,故![]() 舍去……………………………………………………(10分)
舍去……………………………………………………(10分)
把![]() 代入前式得:
代入前式得:![]() ……………………………………………(11分)
……………………………………………(11分)
∴![]()
答:所求抛物线的解析式为![]() 。……………………………(12分)
。……………………………(12分)
26、解:(1)当0≤![]() <4时,如图1,由图可知OM=
<4时,如图1,由图可知OM=![]() ,设经过
,设经过![]() 秒后,正方形移动到
秒后,正方形移动到![]()
∵当![]() =4时,
=4时,![]()
∴点![]() 在C点左侧
在C点左侧
∴夹在两平行线间的部分是多边形COQNG,其面积为:
平行四边形COPG-△NPQ的面积。…………………………………(1分)
∵CO=![]() ,OD=
,OD=![]()
∴四边形COPG面积=![]() ………………………………………………(2分)
………………………………………………(2分)
又∵点P的纵坐标为![]() ,代入
,代入![]() 得P(
得P(![]() ,
,![]() )
)
∴DP=![]() ,NP=
,NP=![]()
由![]() 知:NQ=2NP
知:NQ=2NP
∴△NPQ面积=![]() ·NP·NQ=
·NP·NQ=![]()
∴![]() =
=![]() -
-![]() =
=![]() -
-![]() =
=![]() ……(6分)
……(6分)


(2)当4≤![]() ≤5时,如图2,这时正方形移动到
≤5时,如图2,这时正方形移动到![]()
∵当4≤![]() ≤5时,
≤5时,![]() ≤
≤![]() ≤
≤![]() ,点
,点![]() 在C、O点之间
在C、O点之间
∴夹在两平行线间的部分是![]() ,即平行四边形COPG被切掉了两个小三角形△NPQ和△
,即平行四边形COPG被切掉了两个小三角形△NPQ和△![]() ,其面积为:
,其面积为:
平行四边形COPG的面积-△NPQ的面积-△![]() 的面积………(7分)
的面积………(7分)
与(1)同理,![]() ,
,![]() ,
,![]()
∵CO=![]() ,CM=
,CM=![]() ,
,![]()
∴![]() =
=![]() =
=![]() =
=![]() ………………(8分)
………………(8分)
∴![]() …………………(9分)
…………………(9分)
∴![]() =
=![]() -
-![]() -
-![]()
=![]() -
-![]() ………………………………(10分)
………………………………(10分)
=![]() -
-![]()
=![]() -
-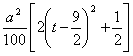
∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() =
=![]() -
-![]() =
=![]() …………(12分)
…………(12分)