2006年中考数学第一次调研试卷
说明：本试卷分为第Ι卷(选择题)和第Ⅱ卷(非选择题)两部分，共4页，满分130分，
考试时间90分钟．
注意: 1.本试卷的选择题和非选择题都在答题卡上作答，不能答在试卷上.
2.答卷前，考生务必将自己的姓名、考生号、试室号、座位号、考卷类型用铅笔涂写
在答题卡上.
3.选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；如需
改动，用橡皮擦干净后，再选涂其他答案.
4.非选择题必须在指定的区域内，用黑色字迹的签字笔或钢笔作答，不能超出指定区
域或在非指定区域作答，否则答案无效.
第Ι卷（选择题 共30分）
一．选择题(本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只
有一项是符合题目要求的)．
1． 电影院呈阶梯或下坡形状的主要原因是( ).
A.为了美观 B.盲区不变 C.增大盲区 D.减小盲区
2． 下列事件中是必然事件的是( ).
A.早晨的太阳一定从东方升起 B.佛山的中秋节晚上一定能看到月亮
C.打开电视机，正在播少儿节目 D.张琴今年14岁了，她一定是初中学生
3． A车站到B车站之间还有3个车站，那么从A车站到B车站方向发出的车辆，一共有
多少种不同的车票( ).
A.8 B.9 C.10 D.11
4. 夏天，一杯开水放在桌子上，杯中水的温度T(℃)随时间t变化的关系的图象是( ).
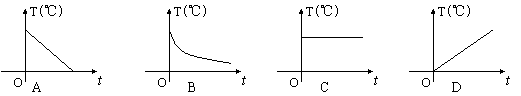
5． 已知直角三角形的两条直角边的长恰好是方程
的两根，则此直角三角
形的斜边长为( ).
A.
B.3 C.
D.13
6． 已知
，则下列四个式子中一定正确的是( ).
A.
B.
C.
D.
7． 抛物线
的顶点坐标是( ).
A.(0，-2) B.(-2，0) C.(0，2) D.(2，0)
8. 
与 -
( ).
A.相等 B.互为相反数 C.互为倒数 D.它们的和为16
9． 如图1，AB是⊙O的直径，C是⊙O上一点，若AC︰BC＝
︰
，AB＝10
，OD
⊥BC于点D，则BD的长为( ).
A.
B.3 C.5
D.6
10．两个完全相同的长方体的长、宽、高分别为5cm、4cm、3cm，
把它们叠放在一起组成一个新的长方体，在这些新长方体中，
表面积最大是( ).
A.
B.
C.
D.
第Ⅱ卷（非选择题 共100分）
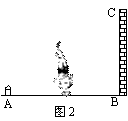二．填空题(本大题共5小题，每小题3分，共15分．把答案填在答题卡相应位置)．
11．回收废纸用于造纸可以节约木材，据专家估计，每回收
一吨废纸可以节约3立方米木材，那么，回收
吨废纸
可以节约 立方米木材.
12．如图2，地面A处有一支燃烧的蜡烛(长度不计)，一个
人在A与墙BC之间运动，则他在墙上的投影长度随着
他离墙的距离变小而 (填“变大”、“变小”或“不变”).
13．“投掷两个骰子，朝上的数字相加为3” 的概率是 .
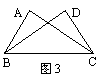
14．如图3，已知AC = BD,要使
≌
，只需增加的一个条件是
.
15．如图4，一个正三角形经过变换依次成为正六边形、正十二边形、正二十四边形、….
当这些正多边形的周长都相等时，正六边形的面积 正十二边形的面积(填不等的
符号).
三．解答题（在答题卷中作答，要有必要的解题步骤．每小题6分，共30分）．
16．化简：
.
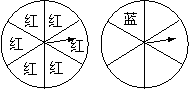
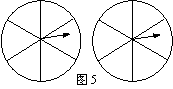17．如图5，用两个相同的转盘(每个圆都平均分成六个
扇形)玩配紫色游戏(一个转盘转出“红”，另一个转
盘转出“蓝”，则为配成紫色).在所给转盘中的扇形
里，分别填上“红”或“蓝”，使得到紫色的概率是
.
18. 某校在一次考试中，甲乙两班学生的数学成绩统计如下：
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 甲 | 1 | 6 | 12 | 11 | 15 | 5 |
| 乙 | 3 | 5 | 15 | 3 | 13 | 11 | |
请根据表格提供的信息回答下列问题：
(1) 甲班众数为______分，乙班众数为______分，从众数看成绩较好的是______班.
(2) 甲班的中位数是_______分，乙班的中位数是______分.
(3) 若成绩在85分以上为优秀，则成绩较好的是______班.
19．画图: 作出线段
的中点
.
（要求：用尺规作图，保留作图痕迹，写出作法，不用证明）.
20．在商品市场经常可以听到小贩的叫嚷声和顾客的讨价还价声：“10元一个的玩具赛车
打八折，快来买啊！”“能不能再便宜2元？”
如果小贩真的让利(便宜)2元卖了，他还能获利20％，根据下列公式求一个玩具赛
车进价是多少元？（公式：
）
四．解答题(直接在卷中作答，要有必要的解题步骤．21、22题各8分，23、24题各9分，
共34分)．
21．完成下表内的解答。
| 题目 | 测量底部可以到达的树木的高 | |||
| 测量目标 |
| |||
| 测得数据 | 测量项目 | AB的长 | 测倾器的高 | 倾斜角 |
| 第一次 | 30米 | AD |
| |
| 第二次 | 40米 | AD |
| |
| 计算 | 求树高BC（精确到0.1米. 用第一次测量数据的计算： 用第二次测量数据的计算： 取平均值，可得这棵树的高大约是 米. 说说你对测量一个物体高度的看法： | |||
1.6米
，
）
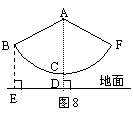22．如图8，秋千拉绳长AB为3米，静止时踩板离地面0.5米，
某小朋友荡该秋千时，秋千在最高处时踩板离地面2米(左右
对称)，请计算该秋千所荡过的圆弧长(精确到0.1米)？
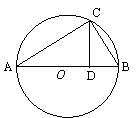
23．已知
内接于⊙O.
(1) 当点O与AB有怎样的位置关系时，∠ACB是直角.
(2) 在满足(1)的条件下，过点C作直线交AB于D，当CD与AB有什么样的关系时，
△ABC∽△CBD∽△ACD.
请画出符合(1)、(2)题意的两个图形后再作答.
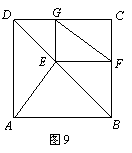
24．如图9，
是正方形
的对角线
上一点，
，
，垂足分别是
.求证：
.
五．解答题（在答题卷中作答,要有必要的解题步骤．25题
10分，26题11分，共21分）．
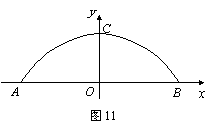
25．一座拱桥的轮廓是抛物线型(如图10所示)，拱高6 m，跨度20 m，相邻两支柱间的
距离均为5 m.
(1) 将抛物线放在所给的直角坐标系中(如图11所示)，其表达式是
的形式.
请根据所给的数据求出
的值.
(2) 求支柱MN的长度.
(3) 拱桥下地平面是双向行车道(正中间是一条宽2 m的隔离带)，其中的一条行车道能否
并排行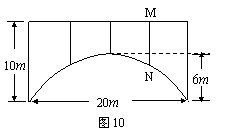
驶宽2 m、高3 m的三辆汽车(汽车间的间隔忽略不计)？请说说你的理由.
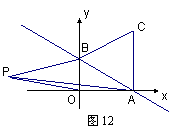26．如图12，一次函数
的图象与
轴、
轴分别交于点A、B，以线段AB
为边在第一象限内作等边△ABC，
(1) 求△ABC的面积；
(2) 如果在第二象限内有一点P（
），试用含的式
子表示四边形ABPO的面积，并求出当△ABP的面
积与△ABC的面积相等时的值；
(3) 在轴上，存在这样的点M，使△MAB为等腰三角形.
请直接写出所有符合要求的点M的坐标.
参考答案
一．选择题（本大题共10个小题，每小题3分，共30分）．
| 题号 | １ | ２ | ３ | ４ | ５ | ６ | ７ | ８ | ９ | 10 |
| 答案 | D | A | C | B | C | C | D | A | B | B |
二．填空题（本大题共5小题，每小题3分，共15分）．
11．
； 12．变小； 13．
； 14．
等； 15．＜．
三．解答题（每小题6分，共30分）．
16．化简：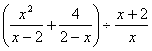
.
解：原式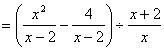
----------------------------3分
----------------------------------------------------------------------------------------------------------------------5分
-----------------------------------------------------------------------------6分
17．解：如图，一个转盘的六个扇形都填“红”，另一个转盘的一个
扇形填“蓝”，余下的五个扇形不填或填其它色.
(注：一个填两个“红”，另一个填三个“蓝”等也可)
18. 解：(1) 90、70、甲. (2) 80、80. (3) 乙. （注：每空1分）
19．解：痕迹正确2分，作法书写正确4分.
20解：设进价是元. ---------------------------------------------------------------------------------------------------------------------------------1分
依题意，得 
. ---------------------------------------------------------------------------------------4分
解得
(元).
答：（略）. -----------------------------------------------------------------------------------------------------------------------------------------------6分
四．解答题（21、22题各8分，23、24题各9分，共34分）．
21．解：用第一次测量数据的计算：
BC＝BE＋EC＝AD＋DE
＝AD＋AB＝1.6＋30·0.600＝19.60. ----------------------------4分
用第二次测量数据的计算：
BC＝BE＋EC＝AD＋DE＝AD＋AB＝1.5＋40·0.466＝20.34. ----------------------------6分
取平均值，可得这棵树的高大约是20.0 米. ----------------------------------------------------------------------------------7分
测量有误差，多次测量可能会减少误差(诸如此类的回答均可). ------------------------------------------------8分
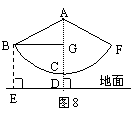22．解：如图，AD垂直地面于D并交圆弧于C，BE垂直地面于E.
根据题设，知BE=2，AC＝3，CD＝0.5(单位：米). ------------------2分
作BG⊥AC于G，
则AG＝AD－GD＝AC＋CD－BE＝1.5. ---------------------------------------4分
由于AB＝3，
所以在直角三角形ABG中，∠BAG＝60°. -------------------------------5分
根据对称性，知∠BAF＝120°. ----------------------------------------------------6分
所以，秋千所荡过的圆弧长是
(米).
答：(略). ---------------------------------------------------------------------------------------------8分
23．解：画图(如右图). ----------------------------------------------------------------------------3分
(1) 当点O在AB上时，∠ACB是直角. ----------------------------------------------5分
(2) 当CD与AB垂直相交于D时，△ABC∽△CBD∽△ACD. ------9分
24．解：连结EC.
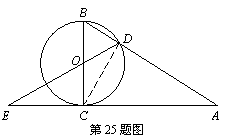∵EF⊥BC，EG⊥CD，∴四边形EFCG为矩形.∴FG=CE. …3分
又BD为正方形ABCD的对角线，∴∠ABE=∠CBE. ………………4分
又BE=BE，AB=CB，∴△ABE≌△CBE. ………………7分
∴AE=EC. ………8分 ∴AE=FG. ………9分
注：对于其它证明方法，请参照给分.
五．解答题（25题10分，26题11分，共21分）．
25．解：(1)根据题目条件，A、B、C的坐标分别是(-10,0)、(0,6)、(10,0). -------------------------------1分
将B、C的坐标代入，得
---------------------------------------------------------------------3分
解得
. ----------------------------------------------4分
所以抛物线的表达式是
. -------------5分
(2) 可设N(5,
)，于是
. -------------------------------------------------------------------------6分
从而支柱MN的长度是
米. ----------------------------------------------------------------------------------------7分
(3) 设DE是隔离带的宽，EG是三辆车的宽度和，则G点坐标是(7,0)(7＝2÷2＋2×3). ------8分
过G点作GH垂直AB交抛物线于H，则
. -------------------------9分
根据抛物线的特点，可知一条行车道能并排行驶这样的三辆汽车. ---------------------------------------------10分
26．解：根据条件，A、B两点的坐标分别是(
)、(
). -------------------------------------------------------1分
(1) 在△ABO中，由勾股定理，得
.
所以正△ABC的高是，从而△ABC的面积是
. ---------------------------------------- 3分
(2) 过P作PD垂直OB于D，则四边形ABPO的面积
. ----------------------------------------5分
当△ABP的面积与△ABC的面积相等时，
四边形ABPO的面积－△AOP的面积＝△ABC的面积，
即
.
解得
. ----------------------------------------------------------------------------------------9分
(3) 符合要求的点M的坐标分别是(
)、(
)、(
)、(
). ------11分