二次函数单元测试
班级 .姓名 .得分 .
一、填空题：（每小题3分，共27分）
1、当m＝____时，函数
是二次函数．
2、抛物线
的顶点坐标是______，对称轴是_____，开口向_____。
3、把
化为
的形式，
=_________。
4、将抛物线
向右平移2个单位后，在向下平移5个单位后所得抛物线顶点坐标为_______。
5、抛物线
经过点（3，5），则
= ；
6、抛物线
，若其顶点在
轴上，则
．
7、已知二次函数
，则当 时，其最大值为0．
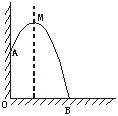
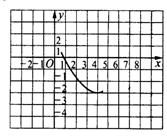
8、抛物线如图所示：当=_______时，=0，当_____时，
>0；当x_____时，<0；
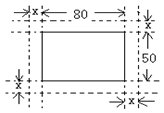9、如图：在一幅长80cm，宽50cm的矩形风景画的四
周镶一条金色纸边，制成一幅矩形挂画，设整个挂画总
面积为ｙcm2，金色纸边的宽为ｘcm，则ｙ与ｘ的关系式
是___________________．
二、选择题（每小题4分，共32分）
1、下列函数中，图象一定经过原点的函数是 （ ）
A. 
B.
C.
D.
|
|
|
|
2、函数
的图象大致为 （ ）
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
|
|
|
|
|
|
|
|
A B C D
3、已知抛物线
的部分图象（如图所示），图象再次与轴相交时的
坐标是（ ） A、（5,0） B、（6,0） C、（7,0） D、（8,0）
4、对于
的图象下列叙述正确的是（ ）
A、的值越大，开口越大 B、的值越小，开口越小
C、的绝对值越小，开口越大 D、的绝对值越小，开口越小
5、二次函数
的图象如右图所示，
|
A a>0 b<0 c>0 B a<0 b<0 c>0
C a<0 b>0 c<0 D a<0 b>0 c>0
6、如图，铅球运动员掷铅球的高度y(m)与水平距
离x(m)之间的函数关系式是 y =－
x2+
x+
，
则该运动员此次掷铅球的成绩是( )
A.6 m B.12 m C.8 m D.10 m
7、函数y=ax2-a与y=a/x(a≠0)在同一直角坐标系中的图象可能是（ ）
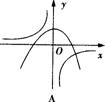
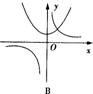
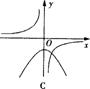
A B C D
|
点M离墙1m，离地面
m，则水流落地点B离墙的距离OB是（ ）
A.2 m B.3 m C.4 m D.5 m
三. 解答题.(共41分)
1、已知抛物线ｙ＝ax2＋（b—1）x+2的图象经过点（1，4），（—1，2），求抛物线的解析式。（本小题7分）
2、某商场以每件20元的价格购进一种商品，试销中发现，这种商品每天的销售量m(件)与每件的销售价x(元)满足关系：m=140－2x.
(1)写出商场卖这种商品每天的销售利润y与每件的销售价x间的函数关系式;
(2)如果商场要想每天获得最大的销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？（本小题8分）
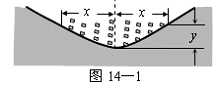4、如图14—1是某段河床横断面的示意图.查阅该河段的水文资料，得到下表中的数据：
| x/m | 5 | 10 | 20 | 30 | 40 | 50 |
| y/m | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
（1）请你以上表中的各对数据（x，y）作为点的坐标，
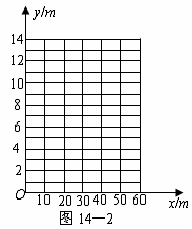尝试在图14—2所示的坐标系中画出y关于x的函数图象；
（2）①填写下表：
| x | 5 | 10 | 20 | 30 | 40 | 50 |
|
|
②根据所填表中数据呈现的规律，猜想出用x表示y 的二次函数的表达式： .
（3）当水面宽度为36米时，一艘吃水深度（船底部到水面的距离）为1.8米的货船能否在这个河段安全通过？为什么？（本小题8分）
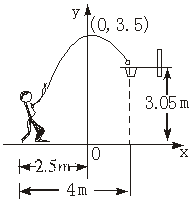
4、如图，一位运动员在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系，求抛物线的表达式;
(2)该运动员身高1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少. （本小题8分）
6、如图，在一块三角形区域ABC中，∠C=90°，边AC=8，BC=6，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上。
⑴求△ABC中AB边上的高h;
⑵设DG=x,当x取何值时，水池DEFG的面积最大？
⑶实际施工时，发现在AB上距B点1.85的M处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为保护大树，请设计出另外的方案，使三角形区域中欲建的最大矩形水池能避开大树。（本小题10分）