初三数学练习（一）
（时限120分钟，满分120分）
一. 选择题（本大题共6小题，每小题3分，共18分）
下列各题：每题都给出A、B、C、D的四个结论，其中只有一个是正确的。
1. 已知圆O1的直径是6cm，圆O2的直径是8cm，
，则圆
和圆
的位置关系是（
）
A. 相交 B. 外离 C. 内切 D. 外切
2. 下列计算错误的是（ ）
A. 
B. 
C. 
D. 
3. 如果用□表示一个小正方体，用
表示两个小立方体的叠加，用■表示三个小立方体的叠加，那么由几个小立方体叠成的几何体从上面看可画成的平面图形是（）
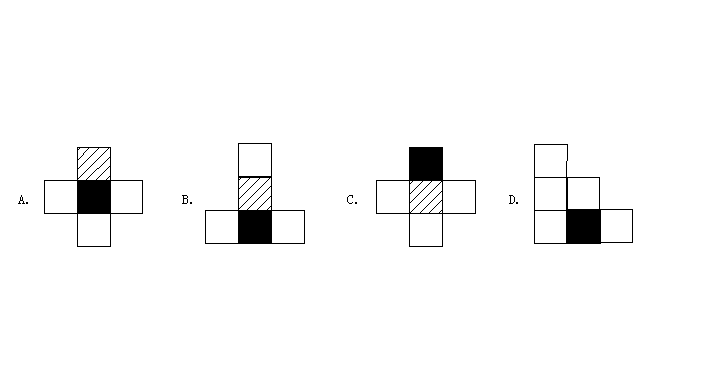
4. 如图是一个水槽，水槽里有一个水杯，将水匀速的注入水杯，水杯满后流入水槽。设注水时间为t，水槽中水的高度是h，则h与t之间的函数图象大致是（）
A B C D
5. 一个口袋中有8个黑球和若干个白球，从口袋中随机摸出一球，记下颜色再放回口袋，不断重复上述过程，共摸了200次，其中57次摸到黑球，因此估计袋中白球为（）
A. 21个 B. 20个 C. 19个 D. 18个
6. 若a、b是实数，且分式
，则
的值是（
）
A. 10 B. 10或2 C. 2 D. 非上述答案
二. 填空题（本题共有6个小题，每小题3分，共18分）
7. 化简
的结果是___________。
8. 某商品的进价是500元，标价是700元，商店要求以不低于5%的利润率打折出售，售货员最低可以打_________折。
9. 将两边长分别是4m和6m的矩形以其一边所在的直线为轴旋转一周，所得的几何体的侧面积是_________cm2。
10. 下表是九年级（1）班20名同学参加某次数学竞赛的成绩统计表。
| 成绩（分） | 60 | 70 | 80 | 90 | 100 |
| 人数（人） | 1 | 5 | x | y | 2 |
若20名学生的平均分是82分，则众数是_________分，中位数是_________分。
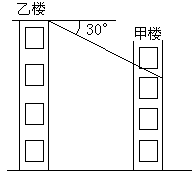
11. 小颖家住在甲楼，她所居住的楼房前面有一座乙楼。冬天，阳光入射角是
，两楼距离20米，小颖家的阳台距地面7米，乙楼高18米，那么影子的顶端距她家阳台还有_________米。（精确到0.1米）
12. 古希腊数学把数1，3，6，10，15，21……叫做三角形数，它有一定的规律性，则第24个三角形数和第22个三角形数的关系是__________________。
三. 作图题（本题满分6分）用圆规和直尺作图，不写作法但要保留作图痕迹。
13. 要把残破的图形模具修复完整，已知弧上三点A、B、C。
（1）找出模具的圆心
（2）若
是等腰三角形，底边
，腰
，求模具的半径R。
四. 解答题（本题满分78分，共有9个小题）
14. 解方程组
（本小题满分6分）
15. （本小题满分6分）
据《中国教育报》2004年5月24日报道，目前全国有近3万所中小学建立了校园网，该报道说，为了了解这3万所中小学校园网建设情况，从中抽取了4600所学校，对它们进行了问卷调查，并根据问卷调查所得的数据绘制了两个统计图。根据上面文字和统计图提供的信息，回答下列问题。
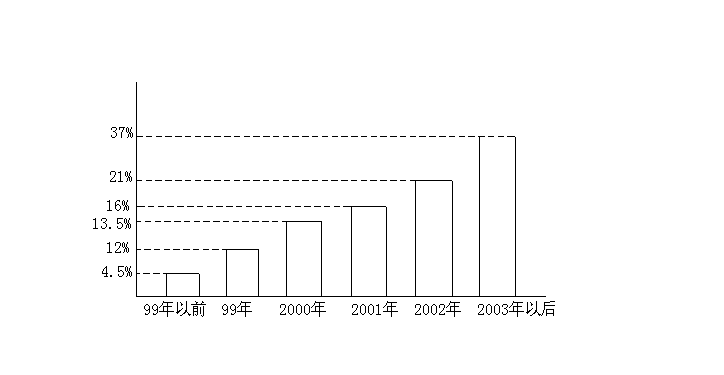
校园网建设时间
校园网资金投入情况（万元）
（1）在问题中总体指什么？样本容量是多少？
（2）估计：在全国中小学已建设校园网的中小学中：
①校园网建设时间在2003年以后（含2003年）的学校大约是多少所？
②校园网建设资金在200万元以上（不含200万元）的学校，大约是多少所？
（3）在抽取的4600所学校中，校园网建设资金投入的中位数落在哪个资金段里？
（4）图中还提供了其它信息。例如，校园网投入在10～50万的学校最多等，请再写上其他两条信息。
16. （本小题满分6分）
请你设计一个“配紫色”的游戏，使配成紫色的概率是
，且每个转盘要分成两份以上。
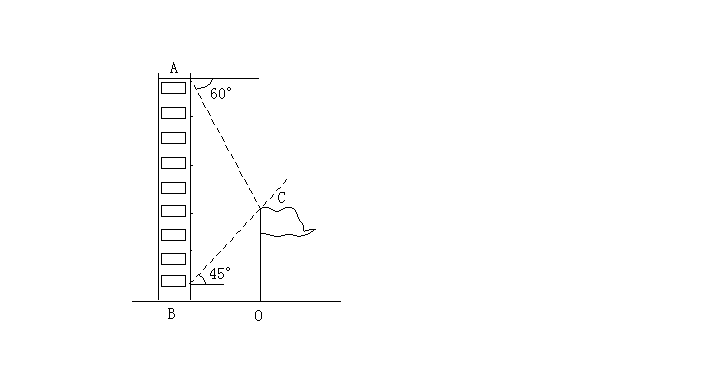
17. （本小题满分8分）
已知小光家住在楼高30米的AB楼上，他从楼顶A测得旗杆顶端C的俯角是
，他又从离地面5米的窗口E处测得旗杆顶端的仰角是
，求旗杆的高度。
18. （本小题满分8分）
国际能源组织（IEA）2004年1月公布的《石油市场报告》预测2004年，中国石油年耗油量将在2003年的基础上继续增加，最多可达3亿吨，将成为全球第二大石油消耗国。已知2003年，中国石油年耗油量大约为2.73亿吨。若一年365天计，石油平均日耗油量以万桶为单位（1吨约合7.3桶）则2004年中国石油平均日耗油量在多少万桶范围内。
19. （本小题满分10分）
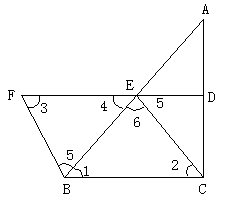
如图，
是直角三角形，
，D、E分别是AC、AB的中点，延长DE到F，使CE=AF。
（1）证明：四边形BCEF是平行四边形。
（2）若四边形BCEF是菱形，则
应为多少度。
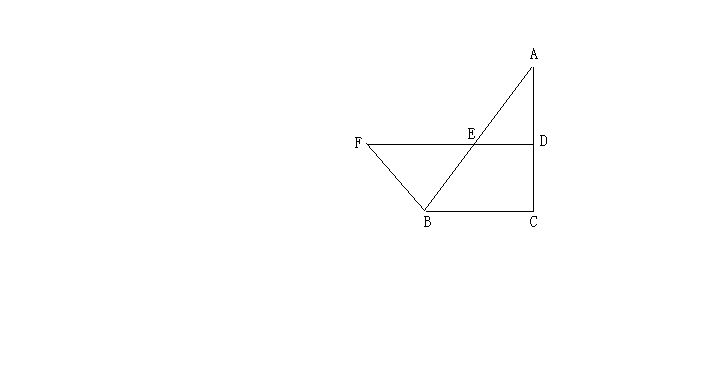
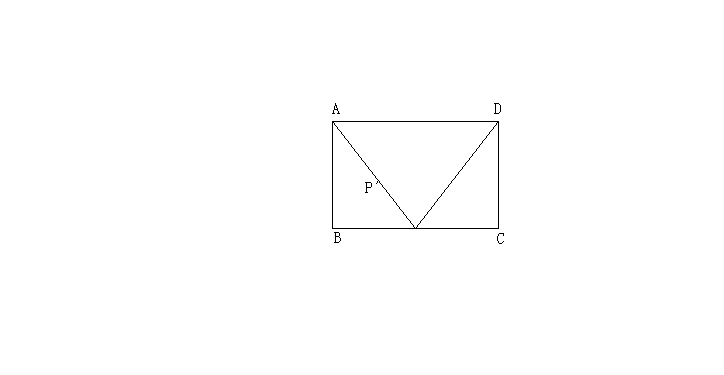
20. （本小题12分）
已知矩形ABCD中，AB=4米，BC=6米，E为BC中点，动点P以2米/s的速度从A出发，沿着
的边，按照
顺序环行一周，设P从A出发经过x秒后，
的面积为y（平方米），求y与x间的函数关系式。
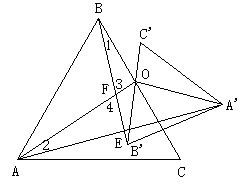
21. 操作：和
都是等边三角形，绕着O点按顺时针方向旋转，O是BC、
的中点，有以下三种图形。
（图1） （图2） （图3）
探究：
（1）在上述三个图形中，AO：BO是否一个固定的值，若是，请选择任意一个图形求出这个比值。
（2）
的值是否也等于这个定值，若是，请结合图（1）证明你的结论。
（3）
与
有怎样的位置关系，请你结合图（2）或图（3）证明你的结论。
【试题答案】
一. 选择题：
1. D 2. C 3. C 4. D 5. B 6. A
二. 填空题：
7. 
8. 7.5折
9. 
或
10. 90，80
11. 0.5
12. 47
13. （1）
（2）连结OA，则
于D
，则
设半径为R，由勾股定理得
14. 解：②×2－①得，
……（3分）
将
代入①得
（5分）
……（6分）
15. 解：（1）总体是3万所中小学建立校园网的建设情况
样本容量是4600……（2分）
（2）①11000所 ②4500所（4分）
（3）中位数落在51～100万资金段中……（5分）
（4）2003年以后建立校园网的学校最多，
投入251～300万和投入300万以上的学校一样多，……（6分）
16. 方案（一）
只要配紫色方案正确就得6分。
17. 解：过C作
于E
，设
……（1分）
在
中，
……（3分）
由题意得，
（米）……（5分）
答：旗杆高为
米。
18. 设2004年平均日耗油x万桶……（1分）
由题意，得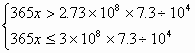
……（3分）
解得
……（5分）
答：2004平均耗油量在546万桶至600万桶之间……（6分）
19. 证明：（1）
是直角三角形
且E是AB中点，
……（1分）
E、D是AC、AB中点，
……（2分）
，
是平行四边形……（4分）
（2）BCEF是菱形，
是
……2分
20. 解：
，E是BC中点
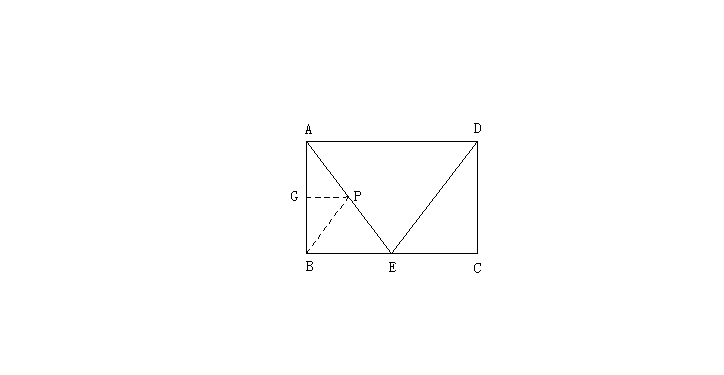
（米）
（1）设
，即P在AE上时，
过P作
，则
……（4分）
（2）若
，即P在DE上
过P作MN平行BC交AB于M，CD于N
则
……（8分）
（3）
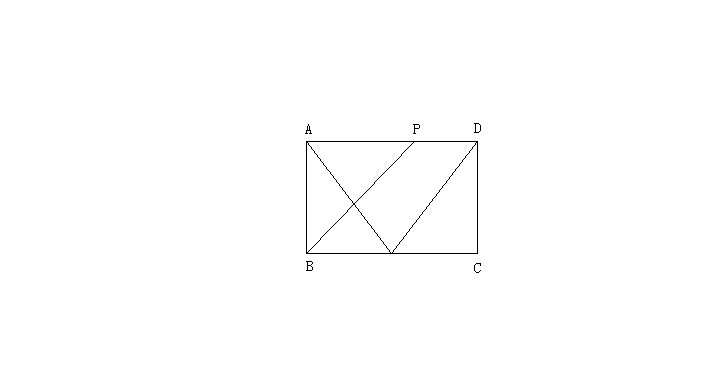
若
，即P在AD上，
……（12分）
21. 证明：（1）
是等边三角形，由图（1）得
……（2分）
（2）
……（8分）
（3）在图（3）中，由（2）得
……（12分）
