初三数学期中考暨第二次月考试卷

2005(下)初三数学期中考暨第二次月考试卷

一、选择题（每题4分，共48分）

1．121的算术平方根是…………………………………………………………………………(　　　 )

A、±11　　　　　　　　　 B、11　　　　　　　　　 C、-11　　　　　　　　　D、±

2．“α的与b的和”用代数式表示为……………………………………………………(　　　　)

A、　　　　　　　B、　　　 C、　　　　　D、

3．抛物线的对称轴是……………………………………………………(　　　　)

A、直线　　　　B、直线　　　C、直线　　　 D、直线

4．今年我国“神六”飞船上，宇航员费俊龙翻了一筋斗，飞船已飞行了35800多千米。用科学计数法表示为……………………………………………………………………………(　　　　)

　A、358×10²千米　　 B、3.58×10²千米　　　　C、3.58×10⁴千米　　　　　　　D、35.8×10³千米

5．已知在△ABC中AB=AC=5，BC=8，则BC边上高AD是……………………………(　　　　)

　A、5　　　　　　　　　　　　B、8　　　　　　　　　　 C、4　　　　　　　　　　 D、3　　　

6．方程组的一个解是………………………………………………………… (　　　　)

　A、　　　　　　　B、　　　　　 C、　　　　　 D、

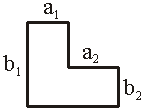7．如图所示阶梯形，将图形分为两个矩形，利用不同分割法可得到不同面积计算方法，数学家阿贝尔从中发现了一个恒等式a₁b₁+a₂b₂=……………………………………………(　　　　)

　A、a₁(b₁-b₂)+(a₁+a₂)b₁

B、a₂(b₁-b₂)+(a₁+a₂)b₂

C、a₁(b₁-b₂)+(a₁+a₂)b₂

D、a₂(b₂-b₁)+(a₁+a₂)b₁

8、口袋中有红球4个，白球3个，黄球2个，黑球1个，从中任摸一球，取得白球概率为(　　　　)

　A、　　　　　　　　　　　　　　B、　　　　　　　　　 C、　　　　　　　　　D、

9、在校运动会上，某运动员标号为数字，结果戴反面了。则裁判看到的是……(　　　　)

　A、　　　　　　　B、　　　　　 C、　　　　　D、

10、在同一直角坐标系中，一次函数和二次函数的图像大致为(　　　　)

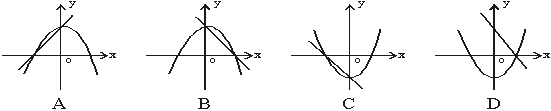
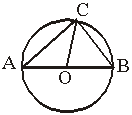11、如图△ABC内接于⊙O，AB经过圆心O，

且，OC=3，则AC长为(　　　　)

　A、3　　　　　　　　　　　　B、6　　　　　　　　　　

C、3　　　　　　　　　D、3　　　 或3

12、设x₁, x₂是关于x的方程的两根，x₁+1，x₂+1是关于方程的两根，则b，c分别是………………………………………………………………(　　　　)

A、1，-3　　　　　　　　　B、1，3　　　　　　　　C、-1，-3　　　　　　 D、-1，3

二、填空题：（每题5分，共30分）

13、因式分解：　　　　　　　　　　　　　　　　　

14、请写出一个解有2的方程　　　　　　　　　　　　　　　 

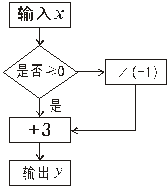
15、在如右图所示运算流程中，

若输出数字，则输入数字

　　　　　　　 

16、如图所示，弓形高CD=1，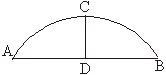

15题图

弦长AB=6，则弓形所在圆半

径r=　　　　　

17、有理数4与9的比例中项是　　　　　　　　　

18、已知，，以为边的三角形是　　　　三角形。

三、解答题（72分）

19、(8分)解不等式组：

20、(8分)计算：

 

 

 

 

 

 

 

 

 

 

21、（12分）按下列要求作图：

（1）在正方形网格中三条不同实线上各取一个格点，使其中任意两点，不在同一实线上。

（2）连结三个格点，使之构成直角三角形（如图1），请在右边网格在作出三个直角三角形，使四个直角三角形互不全等。

  (1)　　　　　　　　 (2)　　　　　　　　 (3)　　　　　　　  (4)

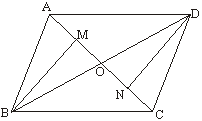
22、（9分）已知：如图在　　ABCD中，对角线AC和BD交于0，M、N分别是OA、OC上点，且　　 （增加一个条件）。求证：BM=DN。

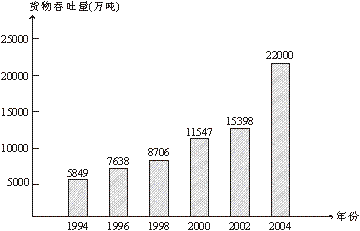
23、（9分）宁波港是一个多功能、综合性的现代大港，年货物吞吐量居中国第二，世界第五，成功跻身国际大港行列，如图是宁波港1994年～2004年货物吞吐量统计图。

（1）从图中你能发现哪些信息，请说出两条。

（2）有人断定宁波港货物吞吐量两年间增长率都不超过15%，你认为他的说法正确吗？请说明理由。

24（12分）一边靠学校院墙，其他三边用40米长的篱笆围成，矩形花圃。设矩形ABCD的边AB=X米，面积为S平方米。

（1）求S与X之间的关系式，并说出怎样围才能使花圃面积最大。

（2）设矩形的边BC=Y米，如果X、Y满足关系式X:Y=Y:（X+Y），即矩形为黄金矩形时，求此黄金矩形的长和宽。

25（14分）已知二次函数

(1)　求证：不论取何值，此函数与轴有二个交点。

(2)　设函数图像与轴交于B、C两点，与轴交于A，若S_△ABC=48，求的值。

(3)　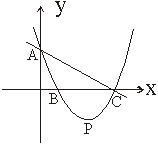设抛物线顶点与P是否存在实数，使△PBC是等腰直角三角形。如果存在，求出的值；如果不存在，说明理由。

2005(下)初三数学期中考暨第二次月考试卷

参　考　答　案

一、选择题(4分×12)

1、B　2、A　3、B　4、C　5、D　6、C　7、C　8、A　9、B　10、B　11、C　12、C

二、填空题(5分×6)

13、　　14、(略)　　15、±5　　16、5　 17、±6　18、直角

三、解答题(72分)

19、解：由①式得X<-2………………2分

　　　　由②式得：X≤1……………2分

　……2分

由图得不等式解为X<-2………………2分

20、(2005²-1)⁰-+(2-)^-1

=1-3+2+………………6分

=3-2 ………………………2分

21、提示：三角形边长只能是，其中能组成直角三角形有：

(1) 　　　　　　　　(2)　　  (3)　　　　　(4)

(5)(已作)　　　(6)　　　　　 (7)　　(8)

(9)　 每对一图得4分

22、条件(2分)　　证明：7分(略)

23、(1)合理信息每条2分，共4分　　(2)说法错误　1分

理由：因为2002~2004年增长率为(或2000-2002、1994-1996)

24、解：(1)S=x(40-2x)=-2x²+40x

=-2(x-10)²+200………………得3分　

∴当x=10时，S最大

即使矩形花圃边AB为10米时，面积最大 ………………得2分

(2)由题意得：y=40-2x………………得1分

∵x：y=y：(x+y)

∴x：(40-2 x)=(40-2x)：(x+40-2x)…………得1分

解得：x₁=20+4　 x₂=20-4…………得2分

当x=20+4时，y=40-2x=-8不合实际舍去…………得1分

∴x=20-4，y=40-2x=8………………得1分

答：黄金矩形长为8米，宽为(20-4)米

25、(1)证明：∵△=[-(m²+8)]²-4×1×2(m²+6)

　　　　　　　  =m⁴+8m²+16

　　　　　　　  =(m²+4)>0

∴此函数与X轴有二个交点…………得4分

(2)解：令y=0，x2-(m²+8)x+2(m²+6)=0

∴x₁=m²+6　 x₂=2

∵m²+6>2

∴B坐标(2，0)　C坐标为(m²+6，0)………………得2分

令x=0得：y=2m²+12即A坐标为(0，2m²+12)…………得1分

∴BC=m²+4　AO=2m²+12

∴S△_ABC=×(m²+4)(2m²+12)=48

∴m=±………………得2分

(3)假设存在P使△PBC是等腰直角三角形，由得P点坐标为()过P作PD⊥X轴于D，则PD==，由抛物线轴对称性得PB=PC。………………得2分

∴∠BPC=90°　∴PD=BC

即=此方程无实根　 …………2分

∴不存在实数m　使△PBC为等腰直角三角形………………1分