初四数学3月月考

		○　　　○　　  ○　　 ○　　（装　　 订　　 线　　 内　　 不　　 要　　 答　　 题）　　○　　　 ○　　  ○
	年　班
	姓　名
△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△

2004-2005学年第二学期初四数学三月份月考

一、单项选择题（每题3分，共30分）----相信你一定能选对！

1．2003年3月末,我国城乡居民储蓄存款余额达94600亿元，用科学记数法表示为（　　）

　　A．94.6×10²　　　 亿元　　　　　　　B．9.46×10³亿元

C．9.46×10⁴亿元　　　　　　　　　　　　　 D．0.946×10⁵亿元

2．在下列图案中，有且只有三条对称轴的是（　　）

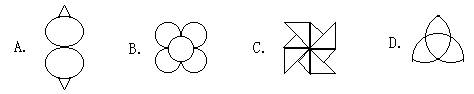
3.用两 块全等的含30°的三角板拼成不同形状的平行四边形，共可以拼成(　)

　A．1个　B　　2个　　　C　3个　　D　　4个

4.甲、乙、丙三位同学进行立定跳远比赛，每人轮流跳一次称为一轮，每轮按名次从高到低分别得3分、2分、1分(没有并列名次)，他们一共进行了五轮比赛，结果甲共得14分；乙第一轮得3分，第二轮得1分，且总分最低.那么丙得到的分数是(　　 )

(A) 8分　　　　  (B) 9分　　　　(C) 10分　　　　　 (D)11分

5.某超市推出如下优惠方案：（１）一次性购物不超过2００元不享受优惠。（２）一次性购物超过2００元，但不超过4００元一律8折，（３）一次性购物超过4００元一律7折。王波两次购物分别付款192元、392元。如果他一次性购买与上两次相同的商品，则比分两次购买省多少钱　　（　　　　）

Ａ188元　Ｂ　　３57.6元　　Ｃ　24或57.6元　　Ｄ188或216元

6、火车票上的车次号有两个意义，一是数字越小表示车速越快，1～98次为特快列车，101～198次为直快列车，301～398次为普快列车，401～498次为普客列车；二是单数与双数表示不同的行驶方向，其中单数表示从北京开出, 双数表示开往北京，根据以上规定，大庆开往北京的某一直快列车的车次号可能是(　　　 )

(A)　20　　(B) 119　 (C)　120　 (D)　319

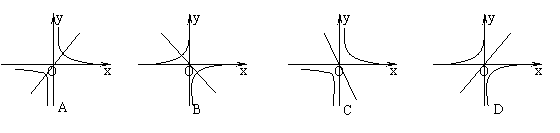
7.在同一直角坐标系中，函数y=3x与y=图象大致是

8方程= 2有且只有一个根，则a的值 为（　　 ）

A　3　　 B　4　　　　C　3或4　　D　 3或 –4

9. 如图，已知⊙的半径为5，点A到圆心O的距离

为3，则过点A的所有弦中，最短弦的长为

（A）4　　　　　　　  （B）6 　　　　　 

（C）8　　　　　　 　 （D）10

10. 平行四边形ABCD中的面积为72，AE：EB= 1：2　

CF：FB=1：2,　则三角形DEF的面积为_________

 （A） 36　 （B） 30　 （C）32　　（D）34

二、填空题（每题3分，共30分）-----积极思考，细心！

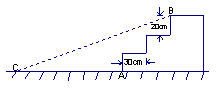
1． 如图，苏州某公园入口处原有三阶台阶，每级台

阶高为

1题

20cm,深为30cm.为方便残疾人士，拟将台阶

改为斜坡，设台阶的起点为A，斜坡的起始点为C，

现将斜坡的坡角∠BCA设计为30°，那么AC的长度为_________

2某城市自来水收费实行阶梯水价，收费标准如下表所示，某户5月份交消费45元，

则所用水为______________吨

月用水量	不超过12度部分	超过12度不超过18度部分	超过18度部分
收费标准（元/吨）	2.00	2.50	3.00

3、已知4^m=a,4ⁿ=b,则4^2m+n-1=　　　　　  (用含a,b的代数式表示)

4.　若代数式x²+3x-5的值为2，则代数式2x²+6x-3的值为　　　　  .

5. 某人在一次买卖中，同时卖出两件衣服，每件240元，按成

本计算，其中一件赔 20%，另一个赚20%，则他在本次经营

活动中___________

6. 菱形ABCD中，边长为10，sin∠1　= 　 点E在对角线

AC上，使AE= AB，点P是BE上任意一点，过点P作PF⊥

BE于点F，过点P作PG⊥AB于G，则PF+PG = ————

7. 第二象限内的点P是抛物线 — 2上的一点，且点PX轴和到Y轴的距离相等，则点P的坐标为___________

8. 一组数据5 ，5， X　 3X　 20 中，正整数X是众数， 则这

组数据的中位数是_______

9. 将两个正方形叠放在一起，∠BAD+∠EAG　= __________

10. 不经过第四象限，则_________

三、简要回答下列问题--------很简单，你能行！(　満分60分　)

1.（本题5分）先化简再求值： ÷（x － 3　－　）其中x　＝　－5

2.（本题6分）

已知x_1,x₂是一元二次方程的两个实数根.

（1）　　 是否存在实数k，使成立？若存在，

求出k的值；若不存在，请说明理由.

（2）求使  的值为整数的实数k的整数值 .

.

3、(本题6分)

一次数学活动课，老师组织学生到野外测量一个池塘的宽度（即图中A、B间的距离）。

在讨论探究测量方案时，同学们发现有多种方法，现请你根据所学知识，设计出两种

测量方案，要求画出测量示意图，并简要说明测量方法和计算依据。

例案：在A处测出∠BAE=90º，并在射线

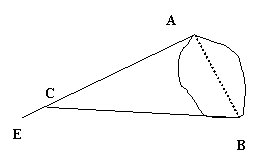AE上的适当位置取点C，量出AC，BC的长度；

运用勾股定理，　得AB=

　 

方案一　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　 

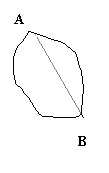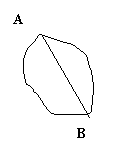方案二：　　　　　　　　　　　　　　

4（本题7分）

 下图是甲 乙两名同学对本班期末考试成绩的统计（分数是整数），

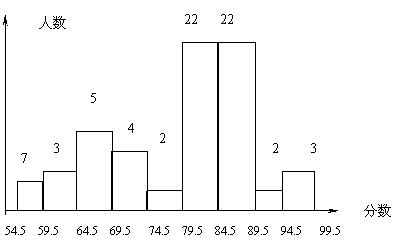
分数	人数
54.5-59.5
59.5-64.5	3
64.5-69.5	5
69.5-70.5
70.5-74.5	3
74.5-76.5	2
76.5-79.5
79.5-82.5	18
82.5-84.5	4
84.5-88.5
88.5-89.5
89.5-94.5	2
94.5-99.5	3
9.5-100.5	0

　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　

　　　　 

　　　　　　　　　　　 　　　　　 

　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　 　　　　　　　

　　　　　　　　　　　　　　　　　　

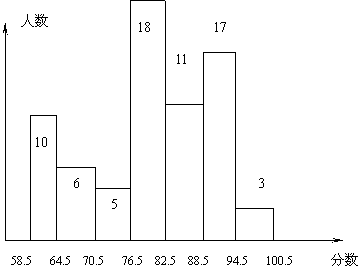
82分的频数为12人，

求（1）根据所给频率分布表填写下列表格

（2）众数是多少？中位数是多少？？

（2）80分（含80分）以上为优秀，优秀率是多少？

（3）及格率是多少 ？

5（本题8分）

图中表示甲 乙两名选手在一次自行车越野赛中，路程Y（千米）随时间X（秒）的变化图象（全程），根据图象回答下列问题：

1） 比赛全程是多少？

2） 两人第一次相遇是在什么时间 ？

3） 乙几分钟走完全程？

（注：粗线为甲，细线为乙，且乙的行驶速度保持不变）

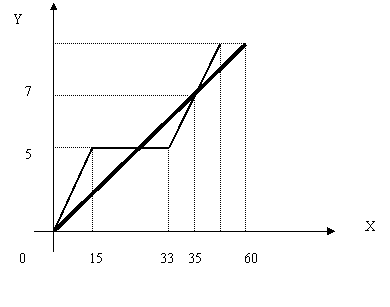6（本题8分）

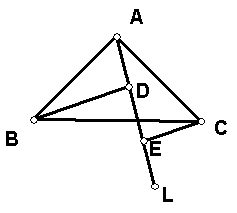
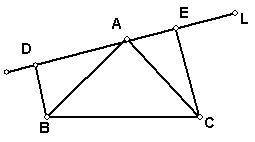
如图1：在△ABC中，∠BAC=90°，AB=AC，L是经过点A的一条直线，且B，C在

L的异侧，BD⊥L于D，CE⊥L于E，易证DE = BD- CE

（1）　　　当直线 L绕点A旋转到图2位置时，DE，BD，CE这间关系如何？写出你的猜想，

并证明。

（2）当直线L绕点A旋转到图3位置时，∠1 = ∠2　∠3 = ∠4， BD， DE，CE之间的关

　系又如何？写出猜想，不用证明。

图1

图2

图3

7．（本题10分）

某中学为筹备校庆活动，准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸，其中4张为彩页，6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩页300元/张，黑白页50元/张；印刷费与印数的关系见下表。

印数a　 (单位：千册)	1≤a＜5	5≤a＜10
彩色 (单位：元/张)	2．2	2．0
黑白（单位：元/张）	0．7	0．6

（1）印制这批纪念册的制版费为　　 元；

（2）　　  若印制2千册，则共需多少费用？

（3）　　  如果该校希望印数至少为4千册，总费用至多为60000元，求印数的取值范围。

（精确到0.01千册）

8：（本题10分）

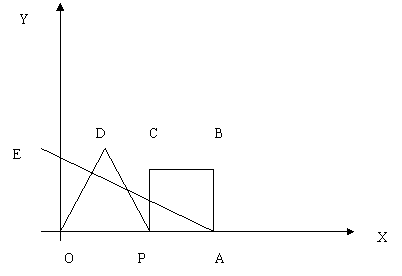
如图所示：直线 AE与X轴正半轴，Y轴正半轴分别交于点A和E,且线段OA，OE的长是关于X的方程的两个根，（OE＜OA＝，且点P为线段OA上从点O向点A运动的一动点，（ 点P不与点A重合），且点P的运动速度 是2厘米/秒，设点P的由点O出发的运动时间为t 秒，当点P运动时，以OP为边长的等边三角形OPD和以PA为边长的正方形ABCP与随之变化，点B，D在第一象限

（1）　　　求直线AE的解析式

（2）　　　当点P运动时，AE与PO的位置关系如何？

（3）　　　是否存在t值， 使得直线BD与X轴交角为30°，若存在，请求出t值，若不存在，请说明理由？

答案

一、　　　　　　 选择题

1　 C　　2　 D　 3　C　 4 B　 5　C　 6　C　　7 D　　8　 C　9  C　10　C

二、　　　　　　 填空题

(1)　AC的长度（60－60）cm（最终结果中不含单位，扣1分）　　　　　　　　 　　　　　　　　　　 (2)　 20　　 ( 3 )　　 　 (4 ) 11　 ( 5) 赔20　 (6 ) 3　

 (7)　 （-2，2）　(8)  10或20　 元　　(9)　 180°　 (10)　3<m≤4

三　1　

2　解：一元二次方程有两个实数根　　

则有K0且△=（-4K）²- 44K(K+1)=-16K≥0　　 ∴k＜0　　　　 

又∵x_1,x₂是一元二次方程　的两个实数根.

 ∴　

∴

　　　　　　　　　　 　　　　=

　 　　　　　　　　　　　　　=2×1²－9× =

若 　则有　=　∴ k=　 而 k＜0

 ∴不存在实数k,使成立

3、只要画出合理的图形，切实可行即可，酌情给分

4　 7　 1　3　　7　 15　　　89　　82　　 70%　　90%

5　 （1）12　（2）　 25 （3）　 50

 6  （1）DE= BD+CE　证明略（2） BC= BD+CE

7。解：（１）１　５００（元）　　（２分）

（２）若印制2千册，则印刷费为：（２.2×4+0.7×6）×2 000=26 000 (元) 　　（１分）

∴总费用为：26 000+1 500=27 500　 (元）　（１分）

(3)设印数为x千册，

①若4≤x＜5，由题意，得

1 000 ×(2.2×4+0.7×6) x+1 500≤60 000

解得x≤4。5　　　（１分）

∴4≤x≤４。5

②若x≥５，由题意，得

1 000×(2.0×4+0.6×6) x+1500≤60 000

解得x≤5。04　　　（１分）

∴5≤x≤5。04

综上所述，符合要求的印数x（千册）的取值范围为：

4≤x≤４。5　或　　5≤x≤5。04　　　（１分）

（如果少考虑等号成立情况，统扣１分）

8. (1)　　(2)垂直　 （3）或

由于时间太紧张，如果有不妥的地方，请见谅

	年　班
	姓　名
△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△△