2006年初中毕业生学业考试数学模拟试卷(一)
考生须知:
1.全卷满分为150分,考试时间120分钟.试卷共4页,有三大题,24小题.
2.本卷答案必须做在答题卷的相应位置上,做在试卷上无效.
3.请用钢笔或圆珠笔将姓名、准考证号分别填写在答题卷的相应位置上.
温馨提示:请仔细审题,细心答题,相信你一定会有出色的表现!
试 卷 Ⅰ
一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
1. 4的平方根是( ▲ )
A、 16 B、![]() 16 C、
16 C、![]() 2
D、2
2
D、2
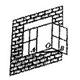 2.
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( ▲ )
2.
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( ▲ )
A、两点之间线段最短
B、三角形的稳定性
C、两点确定一条直线
D、垂线段最短
3. 某物体的三视图是如图所示的三个图形,那么该物体形状是(▲ )
A.
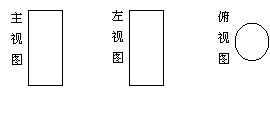 长方体
长方体
B. 圆锥体
C. 立方体
D. 圆柱体
4. 今年6月5日是第33个世界环境日,其主题是“海洋存亡,匹夫有责”.目前全球海洋总面积约为36105.9万平方公里,用科学记数法(保留三个有效数字)表示为( ▲ )
A.3.61×108平方公里 B.3.60×108平方公里
C.361×106平方公里 D.36100万平方公里
5.
要使二次根式![]() 有意义,字母x必须满足的条件是( ▲ )
有意义,字母x必须满足的条件是( ▲ )
A.x≥![]() B.x>-
B.x>-![]() C.x≥-
C.x≥-![]() D.x>
D.x>![]()
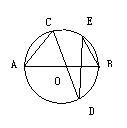
6.下列轴对称图形中(如图),只有两条对称轴的图形是( ▲ )
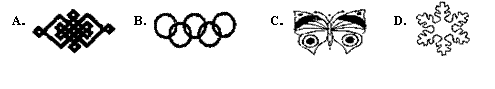
 |
7. 如图,AB为⊙O 的直径,点 C、D、E均在⊙O
上,且∠ACD=60![]()
![]() ,那么∠BED的度数是( ▲ )
,那么∠BED的度数是( ▲ )
A、20![]() B、30
B、30![]()
C、40![]() D、50
D、50![]()
8. 如图,a<0,b>0,c<0,那么二次函数y=ax2+bx+c的图象可能是( ▲ )
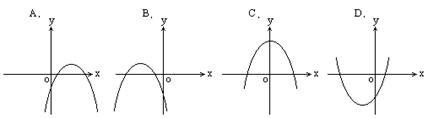
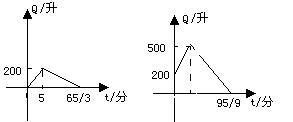 |
9. 有一个装有进、出水管的容器,单位时间内进、出的水量都一定.已知容器的容积为600升,又知单开进水管10分钟可把容器注满,若同时打开进、出水管,20分钟可把容器的水放完.现已知水池内有水200升,先打开进水管5分钟,再打开出水管,两管同时开放直至把容器中的水放完,则能正确反映这一过程中容器的水量Q(升)随时间t(分)变化的图象是( ▲ )
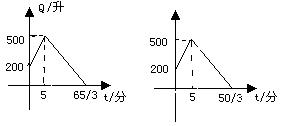
.
10.已知1号、4号两个正方形面积和为7,2号、3号两个正方形面积和为4,则三个正方形a,b,c面积和为(▲ )
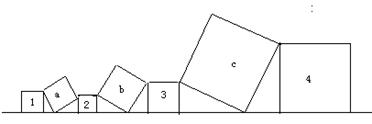 |
A. 11 B 15 C 10 D 22
试 卷 Ⅱ
请将本卷的答案或解答过程用钢笔或圆珠笔写在答卷上.
![]() 二、填空题(本题有6小题,每小题5分,共30分)
二、填空题(本题有6小题,每小题5分,共30分)
 11. 某班55名学生在综合知识竞赛中,分数段在90~100分的频率为0.36,则该班在这个分数段的学生有
▲
人.
11. 某班55名学生在综合知识竞赛中,分数段在90~100分的频率为0.36,则该班在这个分数段的学生有
▲
人.
12.一元二次方程 x(x-1)+3(x-1)=0 的
解是 .
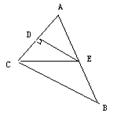
13. 如图,ED为△ABC的边AC上的中垂线,且AB=5,△BCE的
周长为8,则BC= ▲ .
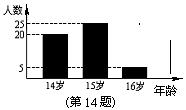
14. 小李将全班同学的年龄情况绘制成了条形统计图(如右图
所示),则该班同学年龄的众数是 ▲ 岁,平均数是 ▲ 岁.
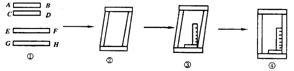 15...工人师傅做铝合金窗框分下面三个步骤进行:先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH, (2)摆放成如图②的四边形,则这时窗框的形状是 ▲ 形,根据的数学道理是:
▲
;(3)将直角尺靠紧窗框的一个角(如图③).调整窗框的边框,当直
15...工人师傅做铝合金窗框分下面三个步骤进行:先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH, (2)摆放成如图②的四边形,则这时窗框的形状是 ▲ 形,根据的数学道理是:
▲
;(3)将直角尺靠紧窗框的一个角(如图③).调整窗框的边框,当直
 角尺的两条直角边与窗框无缝隙时(如图④),
角尺的两条直角边与窗框无缝隙时(如图④),
说明窗框合格,这时窗框是 ▲ 形,根据的数
学道理是: ▲ ;
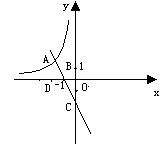
16.. 如图,直线y=-2x-2与双曲线y=k/x交
于点A,与x轴,y轴分别交于点B,C,AD⊥x轴
于点D,如果△ADB的面积与△COB的面积之比等
于4:9![]() ,那么k=__▲_____.
,那么k=__▲_____.
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
 17. (1) 计算: 4
17. (1) 计算: 4![]() +
+![]() ;
;
(2) 先化简再求值:![]() ,其中a=2.
,其中a=2.
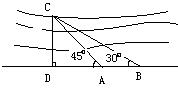
18. 在数学活动上,老师带领学生测河宽.如图, 某学生
在A点观测到河对岸有一点C,并测得∠CAD=45°,
 在距离A点30米的B处测得∠CBD=30°,求河宽
在距离A点30米的B处测得∠CBD=30°,求河宽
CD(结果可带根号)
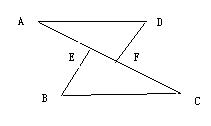
19. 如图,在△AFD和△BEC中,点A、E、F、C在同一直线上,
有下面四个论断:(1)AD∥BC,(2)AE=CF,
(3)∠B=∠D,(4)AD=BC.请用其中三个作为条件,
余下一个作为结论,编写一道数学题,并写出证明过程.
20. 右图是一个正方形花坛的设计图形,空白和阴影两个部份分别种植
不同品种的花卉,请在下列方格中分别设计四种不同的方案,使每
 个图形都有空白部分和阴影部分,且二者的面积之比与右图中两部
个图形都有空白部分和阴影部分,且二者的面积之比与右图中两部
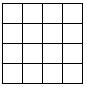 分面积的比相同.
分面积的比相同.



21. 小李和小王用各自的方法,观察并记录了某一天从早上7点整开始的10个小时内,经过学校门口的汽车流量.
小李的方法是:观察记录了每个整点之后十分钟内的车流量,其结果(单位:辆)为:
57,37,50,60,48,30,35,40,70,69.
小王的方法是:观察记录了7点整至9点整这两个小时内的车流量,其结果为489辆.
(1) 按照两人各自的方法,计算这一天在这10个小时内的车流量(精确到10辆);
(2) 你觉得哪种方法更合理?为什么?
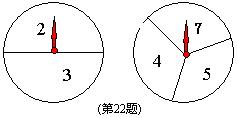
22. 小头爸爸和大头儿子用如图所示的两个转盘做游戏,游戏规则如下:分别转两个转盘,当两个转盘所转到的数字积为偶数时,小头爸爸得1分,当所转到的数字之积为奇数时,大头儿子得1分,这个游戏对双方公平吗?若公平,说明理由.若不公平,如何修改游戏规则才能使游戏对双方公平?
23. 某企业有员工300人,生产A种产品,平均每人每年可创造利润![]() 万元(
万元(![]() 为大于零的常数).为减员增效,决定从中调配
为大于零的常数).为减员增效,决定从中调配![]() 人去生产新开发的B种产品,根据评估,调配后,继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54
人去生产新开发的B种产品,根据评估,调配后,继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54![]() 万元.
万元.
(1)调配后,企业生产A种产品的年利润为_________万元,企业生产B种产品的年利润为_________万元(用含![]() 和
和![]() 的代数式表示).若设调配后企业全年总利润为
的代数式表示).若设调配后企业全年总利润为![]() 万元,则
万元,则![]() 与
与![]() 之间的关系式为
之间的关系式为![]() =____________.
=____________.
(2)若要求调配后,企业生产A种产品的年利润不小于调配前企业年利润的![]() ,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案
?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字).
,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案
?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字).
(3)企业决定将(2)中的年最大总利润(设![]() =2)继续投资开发新产品.现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:
=2)继续投资开发新产品.现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:
| 产 品 | C | D | E | F | G | H |
| 所需资金(万元) | 200 | 348 | 240 | 288 | 240 | 500 |
| 年 利 润(万元) | 50 | 80 | 20 | 60 | 40 | 85 |
如果你是企业决策者,为使此项投资所获年利润不少于145万元,你可以投资开发哪些产品?请写出两种投资方案。
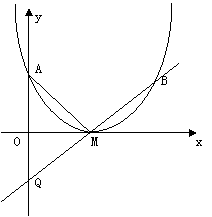
24. 如图,抛物线y=ax2+bx+c的顶点M在x轴上,与y轴交于A点,且2ac+b=0,AM=3,若直线y=3ax+k过M点与抛物线交于B点,与y轴交于Q点;
⑴分别求出二次函数和一次函数的解析式;
⑵以AB为直径作⊙O1,试判断该圆与两坐标轴的位置关系;
⑶过Q点作⊙O1的切线,切点为N,切线交过B点与y轴平行的直线于P,求QN·NP的值.
 |