湖北省荆门市二00六年初中升学考试数学试卷(附评分标准)
人教大纲版.总分120分,考试时间120分钟
一选择题(本大题共10小题,每小题2分,满分20分)
每小题只有一个正确答案,请将选出的答案代号填入题后的括号内.
1.点A在数轴上表示+2,从点A沿数轴向左平移3个单位到点B,则点B所表示的实数是( )
(A)3. (B)-1. (C)5. (D)-1或3.
 2.当m<0时,化简
2.当m<0时,化简![]() 的结果是( )
的结果是( )
(A)-1. (B)1. (C)m. (D)-m.
3.设![]() =a,
=a,![]() =b,用含a,b的式了表示
=b,用含a,b的式了表示![]() ,则下列表示正确的是( )
,则下列表示正确的是( )
(A)0.3ab. (B)3ab. (C)0.1ab2. (D)0.1a2b.
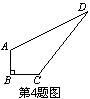
 4.园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
4.园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
(A)24米2. (B)36米2. (C)48米2. (D)72米2.
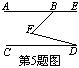
5.如图,直线AE∥CD,∠EBF=135°,∠BFD=60°,则∠D等于( )
 (A)75°.
(B)45°. (C)30°. (D)15°.
(A)75°.
(B)45°. (C)30°. (D)15°.
6.在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是( )
(A)a2-b2=(a+b)(a-b). (B)(a+b)2=a2+2ab+b2.
(C)(a-b)2=a2-2ab+b2. (D)a2-b2=(a-b)2.
7.某市按以下标准收取水费:用小不超过20吨,按每吨1.2元收费,超过20吨则超过部分按每吨1.5元收费.某家庭五月份的水费是平均每吨1.25元,那么这个家庭五月份应交水费( )
(A)20元. (B)24元. (C)30元. (D)36元.
8.某射箭运动员在一次比赛中前6次射击共击中52环,如果他要打破89环(10次射击,每次射击最高中10环)的记录,则他第7次射击不能少于( )
(A)6环. (B)7环. (C)8环. (D)9环.
9.在半径为1的圆中,135°的圆心角所对的弧长为( )
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
10.已知函数y=-kx+4与y=![]() 的图象有两个不同的交点,且A(-
的图象有两个不同的交点,且A(-![]() ,y1)、B(-1,y2)、C(
,y1)、B(-1,y2)、C(![]() ,y3)在函数y=
,y3)在函数y=![]() 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )
(A)y1<y2<y3. (B)y3<y2<y1. (C)y3<y1<y2. (D)y2<y3<y1.
二、填空题(本大题10小题,每小题3分,共30分)
11.举世瞩目的长江三峡水利枢纽工程建成后,总装机容量为1820千瓦,年发电量为847亿千瓦时,将年发电量用科学记数法表示为______千瓦时.
12.计算:(![]() )2=________.
)2=________.
 13.化简:
13.化简:![]() =________.
=________.
14.若方程x2+(m2-1)x+m=0的两根互为相反数,则m=______.
15.一个蓄水池储水20m3,用每分钟抽水0.5m3的水泵抽水,则蓄水池的余水量y(m3)与抽水时间t(分)之间的函数关系式是__________.
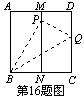
 16.如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=______.
16.如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=______.
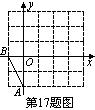
17.在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫格点三角形.在如图5×5的方格中,作格点△ABC和△OAB相似(相似比不为1),则点C的坐标是____________.
18.若(![]() -x)3=a0+a1x+a2x2+a3x3,则(a0+a2)2-(a1+a2)2的值为________.
-x)3=a0+a1x+a2x2+a3x3,则(a0+a2)2-(a1+a2)2的值为________.
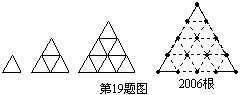
19.如图,是用火柴棒摆出的一系列三角形图案,按这种方案摆下去,当每边上摆2006根火柴棒时,共需要摆________根火柴棒.
20.两圆半径分别为1和7,若它们的两条公切线互相垂直,则它们的圆心距为__________.
三、解答题(本大题共8小题,满分70分)
21.(6分)解不等式组: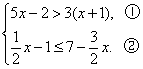
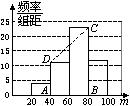
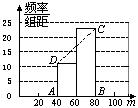
22.(6分)为了增强学生的法制观念,学校举办了一次法制知识竞赛.现将全校500名参赛学生的竞赛成绩(得分取整数)进行随机抽样,并绘制出统计得到的频率分布表和频率分布直方图的一部分.
| 分组 | 频数 | 频率 |
| 0≤m<20 | 0 |
|
| 20≤m<40 | ||
| 40≤m<60 | 11 | 0.22 |
| 60≤m<80 | 23 | 0.46 |
| 80≤m≤100 | 12 | |
| 合计 | 1.00 |
(1)补全频率分布表;
(2)补全频率分布直方图,图中梯形ABCD的面积是______;
(3)估计参赛学生中成绩及格(不低于60分)的人数有多少人?
23.(8分)为了完善城市交通网络,为便市出行,市政府决定修建东宝山交通隧道.现要使工程提前3个月完成,需将原定工作效率提高12%,求原计划完成这项工程需用多少个月?
24.(8分)[尝试]如图,把一个等腰直角△ABC沿斜边上的中线CD(裁剪线)剪一刀,把分割成的两部分拼成一个四边形A′BCD,如示意图(1).(以下有画图要求的,工具不限,不必写画法和证明)
(1)猜一猜:四边形A′BCD一定是__________;
(2)试一试:按上述的裁剪方法,请你拼一个与图(1)不同的四边形,并在图(2)中画出示意图.

[探究]在等腰直角△ABC中,请你沿一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)想一想:你能拼得的特殊四边形分别是________________;(写出两种)
(2)画一画:请分别在图(3)、图(4)中画出你拼得的这两个特殊四边形的示意图.
[拓广]在等腰直角△ABC中,请你沿一条与中线、中位线不同的裁剪线剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)变一变:你确定的裁剪线是________________,(写出一种)拼得的特殊四边形是______;
(2)拼一拼:请在图(5)中画出你拼得的这个特殊四边形的示意图.
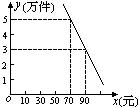 25.(10分)某环保器材公司销售一种市场需求较大的新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售该种产品的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.
25.(10分)某环保器材公司销售一种市场需求较大的新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元)存在如图所示的一次函数关系,每年销售该种产品的总开支z(万元)(不含进价)与年销量y(万件)存在函数关系z=10y+42.5.
(1)求y关于x的函数关系式;
(2)度写出该公司销售该种产品年获利w(万元)关于销售单价x(元)的函数关系式;(年获利=年销售总金额-年销售产品的总进价-年总开支金额)当销售单价x为何值时,年获利最大?最大值是多少?
 (3)若公司希望该产品一年的销售获利不低于57.5万元,请你利用(2)小题中的函数图象帮助该公司确定这种产品的销售单价的范围.在此条件下要使产品的销售量最大,你认为销售单价应定为多少元?
(3)若公司希望该产品一年的销售获利不低于57.5万元,请你利用(2)小题中的函数图象帮助该公司确定这种产品的销售单价的范围.在此条件下要使产品的销售量最大,你认为销售单价应定为多少元?
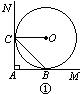
26.(10分)如图①,直线AM⊥AN, ⊙O分别与AM、AN相切于B、C两点,连结OC、BC,则有∠ACB=∠OCB;(请思考:为什么?)如果测得AB=a,则可知⊙O的半径r=a.(请思考:为什么?)
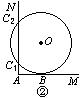 (1)将图①中直线AN向右平移,与⊙O相交于C1、C2两点,⊙O与AM的切点仍记为B,如图②.请你写出与平移前相应的结论,并将图②补充完整;判断此结论是否成立,且说明理由.
(1)将图①中直线AN向右平移,与⊙O相交于C1、C2两点,⊙O与AM的切点仍记为B,如图②.请你写出与平移前相应的结论,并将图②补充完整;判断此结论是否成立,且说明理由.
(2)在图②中,若只测得AB=a,能否求出⊙O的半径r?若能求出,请你用a表示r;若不能求出,请补充一个条件(补充条件时不能添加辅助线,若补充线段请用b表示,若补充角请用α表示),并用a和补充的条件表示r.
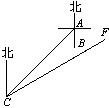 27.(10分)如图,某乡村小学有A、B两栋教室,B栋教室在A栋教室正南方向36米处,在A栋教室西南方向300
27.(10分)如图,某乡村小学有A、B两栋教室,B栋教室在A栋教室正南方向36米处,在A栋教室西南方向300![]() 米的C处有一辆拖拉机以每秒8米的速度沿北偏东60°的方向CF行驶,若拖拉机的噪声污染半径为100米,试问A、B两栋教室是否受到拖拉机噪声的影响?若有影响,影响的时间有多少秒?(计算过程中
米的C处有一辆拖拉机以每秒8米的速度沿北偏东60°的方向CF行驶,若拖拉机的噪声污染半径为100米,试问A、B两栋教室是否受到拖拉机噪声的影响?若有影响,影响的时间有多少秒?(计算过程中![]() 取1.7,各步计算结果精确到整数)
取1.7,各步计算结果精确到整数)
28.(12分)在平面直角坐标系中,已知A(0,2),B(4,0),设P、Q分别是线段AB、OB上的动点,它们同时出发,点P以每秒3个单位的速度从点A向点B运动,点Q以每秒1个单位的速度从点B向点O运动.设运动时间为t(秒).
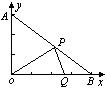 (1)用含t的代数式表示点P的坐标;
(1)用含t的代数式表示点P的坐标;
(2)当t为何值时,△OPQ为直角三角形?
(3)在什么条件下,以Rt△OPQ的三个顶点能确定一条对称轴平行于y轴的抛物线?选择一种情况,求出所确定的抛物线的解析式.
荆门市二00六年初中升学考试
数学试题参考答案及评分说明
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 选项 | B | A | A | B | D | A | C | C | D | B |
二、填空题
11.8.47×1010 12.![]() 13.2 14.-1 15.y=20-0.5t(0≤t≤40) 16.
13.2 14.-1 15.y=20-0.5t(0≤t≤40) 16.![]() 17.(4,0)或(3,2) 18.1 19. 20.6
17.(4,0)或(3,2) 18.1 19. 20.6![]() 或8
或8![]() 或10
或10
说明:17题答对1个给2分,答对2个给3分;20题每答对1个给1分.
三、解答题
 21.解:解不等式①,得x>
21.解:解不等式①,得x>![]() ;解不等式②,得x≤4. …………………………………………4分
;解不等式②,得x≤4. …………………………………………4分
在数轴上表示其解集,如图:![]()
∴不等式的解集是![]() <x≤4. ………………………………6分
<x≤4. ………………………………6分
22. 解:(1)各格依次为4,0.08,0.24,50;………………………………2分
(2)补全直方图如图所示,3分梯形的面积为0.68; …………………………………………4分
(3)![]() ×500=350,(或(0.22+0.46)×500=350)估计及格人数有350人.………………6分
×500=350,(或(0.22+0.46)×500=350)估计及格人数有350人.………………6分
23.解:设原计划完成这项工程需用x个月.依题意得![]() . ………………4分
. ………………4分
化简,得![]() .解得x=28.
.解得x=28.
答:原计划完成这项工程需用28个月.………………………………………………………8分
24.解:[尝试]①平行四边形;1分
②如图(1)所示.3分
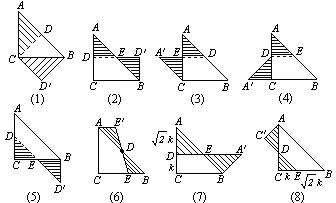
[探究]①平行四边形、矩形或者等腰梯形,(答其中两个即可)……………………………4分
②如图(2)、(3)、(4)、(5)所示.(画其中两个即可)…………………………………………6分
[拓广]①直角梯形,将斜边上的呣绕斜边中点旋转任意角度所得的直线;或者将平行于BC边(直角边)的中位线平移与AC交于点D,使AD:DC=![]() :1的直线;或者将平行于AB边(斜边)的中位线平移与AC交于点D,使AD:DC=
:1的直线;或者将平行于AB边(斜边)的中位线平移与AC交于点D,使AD:DC=![]() :1的直线. ……………………………………7分
:1的直线. ……………………………………7分
说明:裁剪线只答一种即可.其它叙述方式只要表达正确都应给分.
②如图(6)、(7)、(8)所示.(画其中一个即可)………………………………………………8分
25.解:(1)由题意,设y=kx+b,图象过点(70,5),(90,3),
∴![]() 解得
解得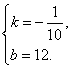 ∴y=
∴y=![]() x+12.…………………………………………3分
x+12.…………………………………………3分
(2)由题意,得w=y(x-40)-z=y(x-40)-(10y+42.5)=(![]() x+12)(x-10)-10(
x+12)(x-10)-10(![]() x+12)-42.5
x+12)-42.5
=-0.1x2+17x-642.5=![]() (x-85)2+80.
(x-85)2+80.
当85元时,年获利的最大值为80万元. ……………………………………………………6分
(3)令w=57.5,得-0.1x2+17x-642.5=57.2.
 整理,得x2-170x+7000=0.
整理,得x2-170x+7000=0.
解得x1=70,x2=100.
由图象可知,要使年获利不低于57.5万元,销售单价应在70元到100元之间.又因为销售单价越低,销售量越大,所以要使销售量最大,又使年获利不低于57.5万元,销售单价应定为70元.………………………………10分
26.解:(1)图②中相应结论为∠AC1B=∠OC1B和∠AC2B=∠OC2B.………………………2分
先证∠AC1B=∠OC1B.连接OB、OC1,
∵AM与⊙O相切于B,∴OB⊥AM.
∵AN⊥AM,∴OB∥AN.∴∠AC1B=∠OBC1.
∵OB=OC1,∴∠OBC1=∠OC1B, ∴∠AC1B=∠OC1B.同理可证∠AC2B=∠OC2B.……4分
(2)若只测得AB=a,不能求出⊙O的半径r.……………………………………………………5分
补充条件:另测得AC1=b.……………………………………………………………………6分
作OD⊥C1C2,则C1D=C2D.
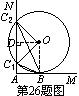 由AB2=AC1•AC2,得AC2=
由AB2=AC1•AC2,得AC2=![]() .则C1C2=AC2-AC1=
.则C1C2=AC2-AC1=![]() -b=
-b=![]() .
.
∴C1D=![]() C1C2=
C1C2=![]() .
.
故r=OB=AD=AC1+C1D=b+![]() =
=![]() .…………………………………………10分
.…………………………………………10分
说明:1.①若补充条件:另测得AC2=b,则r=![]() .②若补充条件:另测得C1C2=b,则r=
.②若补充条件:另测得C1C2=b,则r=![]() .③若补充条件:另测得BC1=b,则r=
.③若补充条件:另测得BC1=b,则r=![]() .④若补充条件:另测得∠ABC1=α,则r=
.④若补充条件:另测得∠ABC1=α,则r=![]() .
.
2.以上答案供参考,若有其他答案,只要正确,都应给分.
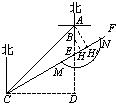 27.解:过点作直线AB的垂线,垂足为D.………………………………………………………1分
27.解:过点作直线AB的垂线,垂足为D.………………………………………………………1分
设拖拉机行驶路线CF与AD交于点E.∵AC=300![]() ,∠ACD=45°,
,∠ACD=45°,
∴CD=AD=300![]() ÷
÷![]() =300.DE=CD•tan30°=300×
=300.DE=CD•tan30°=300×![]() =170.
=170.
∴BE=300-36-170=94.……………………………………………4分
过点B作BH⊥CF,垂足为H,则∠EBH=30°.
∴BH=BE•cos30°=94×![]() =80.∵80<100,∴B栋教室受到拖拉机噪声影响.…………6分
=80.∵80<100,∴B栋教室受到拖拉机噪声影响.…………6分
以点B为圆心,100为半径作弧,交CF于M、N两点,则MN=2![]() =2×60=120.
=2×60=120.
B栋教室受噪声影响的时间为:120÷8=15(秒).……………………………………………8分
作AH′⊥CF,H′为垂足,则∠EAH′=30°.又AE=36+94=130,∴AH′=AE•cos30°=130×![]() =111.
=111.
∵111>100,∴A栋教室不受拖拉机噪声影响.……………………………………………10分
28.解:(1)作PM⊥y轴,PN⊥x轴.∵OA=3,OB=4,∴AB=5.
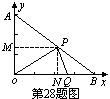 ∵PM∥x轴,∴
∵PM∥x轴,∴![]() .∴
.∴![]() .∴PM=
.∴PM=![]() t.…………2分
t.…………2分
∵PN∥y轴,∴![]() .∴
.∴![]() .∴PN=3-
.∴PN=3-![]() t.
t.
∴点P的坐标为(![]() t,3-
t,3-![]() t). ……………………………………4分
t). ……………………………………4分
(2)①当∠POQ=90°时,t=0,△OPQ就是△OAB,为直角三角形.………………………………5分
②当∠OPQ=90°时,△OPN∽△PQN,∴PN2=ON•NQ.(3-![]() t)2=
t)2=![]() t(4-t-
t(4-t-![]() t).
t).
化简,得19t2-34t+15=0.解得t=1或t=![]() .……………………………………………………6分
.……………………………………………………6分
③当∠OQP=90°时,N、Q重合.∴4-t=![]() t,∴t=
t,∴t=![]() .………………………………………7分
.………………………………………7分
综上所述,当t=0,t=1,t=![]() ,t=
,t=![]() 时,△OPQ为直角三角形.………………………………8分
时,△OPQ为直角三角形.………………………………8分
(3)当t=1或t=![]() 时,即∠OPQ=90°时,以Rt△OPQ的三个顶点可以确定一条对称轴平行于y轴的抛物线.当t=1时,点P、Q、O三点的坐标分别为P(
时,即∠OPQ=90°时,以Rt△OPQ的三个顶点可以确定一条对称轴平行于y轴的抛物线.当t=1时,点P、Q、O三点的坐标分别为P(![]() ,
,![]() ),Q(3,0),O(0,0).设抛物线的解析式为y=a(x-3)(x-0),即y=a(x2-3x).将P(
),Q(3,0),O(0,0).设抛物线的解析式为y=a(x-3)(x-0),即y=a(x2-3x).将P(![]() ,
,![]() )代入上式,得a=-
)代入上式,得a=-![]() .∴y=-
.∴y=-![]() (x2-3x).
(x2-3x).
即y=-![]() x2+
x2+![]() x.……………………………………………………………………………12分
x.……………………………………………………………………………12分
说明:若选择t=![]() 时,点P、Q、O三点的坐标分别是P(
时,点P、Q、O三点的坐标分别是P(![]() ,
,![]() ),Q(
),Q(![]() ,0),O(0,0).求得抛物线的解析式为y=-
,0),O(0,0).求得抛物线的解析式为y=-![]() x2+
x2+![]() x,相应给分.
x,相应给分.
 0
0