06年春九年级升学模拟考试
数学试卷(允许使用计算器)
考试时间:120分钟 总分:150分 得分:A +B
A卷(100分)
一、 选择题 (本大题有12小题,每小题3分,满分36分)
1.3的相反数的倒数是( )
A.-3 B.![]() C.
C.![]() D.3
D.3
2.观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是( )

3.粤海铁路是我国第一条横跨海峡的铁路通道,设计年输送货物能力为11 000 000吨,用科学记数
法应记为( )
A.11×106吨 B.1.1×107吨 C.11×107吨 D.1.1×108吨
4.
把分式方程![]() 的两边同时乘以(x-2), 约去分母,得( )
的两边同时乘以(x-2), 约去分母,得( )
A.1-(1-x)=1 B.1+(1-x)=1 C.1-(1-x)=x-2 D.1+(1-x)=x-2
 5. 如图,
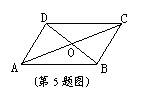
5. 如图,![]() ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取什范围是( ) A.1<m<11
B.2<m<22
ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取什范围是( ) A.1<m<11
B.2<m<22
C.10<m<12 D.5<m<6
6. 函数![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x>3 B.x≥3 C.x>-3 D.x≥-3
7. 从一幅扑克牌中抽出5张红桃,4张梅花,3张黑桃放在一起洗匀后,从中一次随机抽出10张,恰好红桃、梅花、黑桃3种牌都抽到,这件事情( )
A.可能发生 B.不可能发生 C.很可能发生 D.必然发生
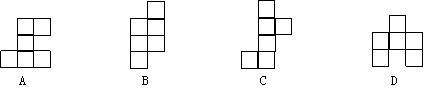
8. 下面的平面图形中,是正方体的平面展开图的是( )
9.
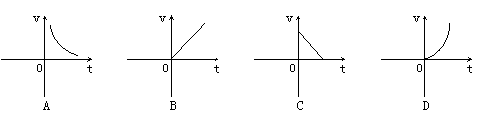 在匀速运动中,路程s(千米)一定时,速度v(千米/时)关于时间t(小时)的函数关系的大致图象是( )
在匀速运动中,路程s(千米)一定时,速度v(千米/时)关于时间t(小时)的函数关系的大致图象是( )
10. 下表是某化妆连锁店05年1至6月份销售额的情况(单位:元)
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | |
| 甲(石板滩店) | 450 | 440 | 480 | 420 | 576 | 550 |
| 乙(泰 兴店) | 480 | 440 | 470 | 490 | 520 | 516 |
根据以上信息可知( ) A.甲比乙的月平均销售量大 B.甲比乙的月平均销售量小 C.甲比乙的销售稳定 D.乙比甲的销售稳定
11.图所示,是两木杆在同一时刻的影子,请问它们是太阳光线还是灯光下的投影?请问这一时刻是上午还是下午? ( )
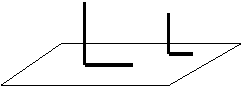 A、太阳光线,上午 B、太阳光线,下午 C、灯光,上午 D、 灯光,下午
A、太阳光线,上午 B、太阳光线,下午 C、灯光,上午 D、 灯光,下午
 |
北
东 西
南
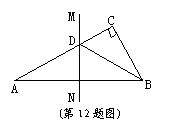
12. 如图,在△ABC中,∠C=90°,AC=8cm, AB的垂直平分线MN交AC于D,连结BD, 若![]() ,则BC的长是( ) A.4cm B.6cm C.8cm D.10cm
,则BC的长是( ) A.4cm B.6cm C.8cm D.10cm
![]()
![]() 二、填空题(本大题有8小题,每小题3分,满分24分)
二、填空题(本大题有8小题,每小题3分,满分24分)
![]() 13.在下面等式的 内填数,
内填运算符号,使等号成立(两个算式中的运算符号不能相同):
13.在下面等式的 内填数,
内填运算符号,使等号成立(两个算式中的运算符号不能相同):
 14. 某商场4月份营业额为x万元,5月份营业额比4月份多10万元. 如果该市场第二季度的营业额为4x万元,那么6月份的营业额为 万元,这个代数式的实际意义是 .
14. 某商场4月份营业额为x万元,5月份营业额比4月份多10万元. 如果该市场第二季度的营业额为4x万元,那么6月份的营业额为 万元,这个代数式的实际意义是 .
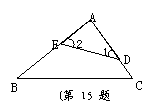
15. 如图,D、E两点分别在AC、AB上,且DE
 与BC不平行,请填上一个你认为合适的条件:
与BC不平行,请填上一个你认为合适的条件:
,使得△ADE∽△ABC.
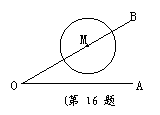
16.如图,已知∠AOB=30°,M为OB边上一点,以M为圆心、
 2cm为半径作M. 若点⊙M在OB边上运动,则当OM=
cm
2cm为半径作M. 若点⊙M在OB边上运动,则当OM=
cm
时,⊙M与OA相切.
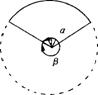
17.如图,扇子的圆心角为α,余下扇形的圆心角为β,为了使扇子
的外形美观,通常情况下α与β的比按黄金比例设计,若制作半径为
30cm的扇子,则扇面弧长为 cm.(精确到个位)
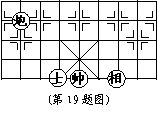 18. 在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红球、两个黄球. 如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄球的概率是
.
18. 在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个红球、两个黄球. 如果第一次先从袋中摸出一个球后不再放回,第二次再从袋中摸出一个,那么两次都摸到黄球的概率是
.
![]()
![]() 19.如图,如果 所 所在位置的坐标为(-1,y),
19.如图,如果 所 所在位置的坐标为(-1,y),
所![]() 在位置的坐标为(x,-2), 那么, 所 所在位置的
在位置的坐标为(x,-2), 那么, 所 所在位置的
坐标为 .
20. 当m =______时,函数![]() 的图象是抛物线,开口向______,有最______值.
的图象是抛物线,开口向______,有最______值.
三、解答题 21.(本题有2小题,每小题4分,满分8分)
(1)
计算:![]()
(2)
先化简,后求值:![]() ,其中
,其中![]()
22. (共4小题,每小题2分,满分8分)图1是某市年生产总值统计图,根据此图完成下列各题:
(1)2003年某市的生产总值达到 亿元,约是1997年的 倍(倍数由四舍五入法精确到个位);
(2)小王把图1的折线统计图改为条形统计图,但尚未完成(如图2),请你帮他完成该条形图;
(3)2003年某市年生产总值与2002年相比,增长率是 %(结果保留三个有效数字);
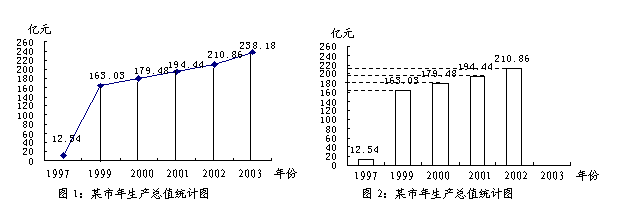 (4)已知2003年某市的总人口是139.19万,则该年某市人均生产总值约是
元(结果保留整数).
(4)已知2003年某市的总人口是139.19万,则该年某市人均生产总值约是
元(结果保留整数).
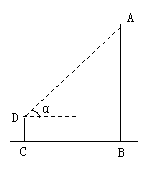 23.(6分)雄伟壮观的“千年塔”屹立在海口市西海岸带状公园的“热带海洋世界”.在一次数学实践活动中,为了测量这座“千年塔”的高度,雯雯在离塔底139米的C处(C与塔底B在同一水平线上),用高1.4米的测角仪CD测得塔顶A的仰角α=43°(如图),求这座“千年塔”的高度AB(结果精确到0.1米).(参考数据:tan43°≈0.9325, cot43°≈1.0724)
23.(6分)雄伟壮观的“千年塔”屹立在海口市西海岸带状公园的“热带海洋世界”.在一次数学实践活动中,为了测量这座“千年塔”的高度,雯雯在离塔底139米的C处(C与塔底B在同一水平线上),用高1.4米的测角仪CD测得塔顶A的仰角α=43°(如图),求这座“千年塔”的高度AB(结果精确到0.1米).(参考数据:tan43°≈0.9325, cot43°≈1.0724)
24.(6分)某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克. 经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克. 现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
25.(6分)已知直线y=-x+2m+1与双曲线y=![]() 有两个不同的公共点A、B.
有两个不同的公共点A、B.
(1)求m的取值范围;(3分)
(2)点A、B能否关于原点中心对称?若能,求出此时m的值;若不能,说明理由.(3分)
26、(6分)如图,已知△ABC,∠ACB=90º,AC=BC,点E、F在AB上,∠ECF=45º,
 (1)求证:△ACF∽△BEC(3分)
(1)求证:△ACF∽△BEC(3分)
(2)设△ABC的面积为S,求证:AF·BE=2S (3分)
B卷(50分)
一、填空题:(本题有5小题,每小题4分,满分20分)
1.关于x的一元二次方程x2-4x + 8sinA = 0的两根相等,且A是锐角,则∠A = _____度.
2.若设石板滩与新都之间有泰兴一个客车中途站,则设计往返于石板滩与新都之间不同的客车车票应有 种?
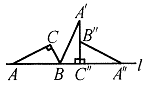
3.如图,把直角三角形ABC的斜边AB放在直
|
△ A"B"C"的位置.设BC=1,![]() ,则顶
,则顶
点A运动到点A"的位置时,点A经过的路线与直
线l所围成的面积是 .(计算结果不取近似值)
4、将一抛物线向右平移3个单位,再向上平移2个单位后,得到抛物线y=![]() x
x![]() ,那么原抛物线是
。
,那么原抛物线是
。
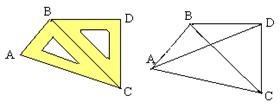
5. 将一副三角尺如图摆放一起,连接AD,则tan∠ADB= 。
二、解答题.
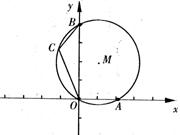
6、(8分)如图,⊙M经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(4,0),C是圆上一点,∠BCO=120°,求⊙M的半径和圆心M的坐标。
7、(11分)如图,已知线段AB上一点O,以OB为半径的⊙O交线段AB于C,以线段AO为直径的半
圆交⊙O于点D,过点B作AB的垂线与AD相交于点E.
①
![]() 求证:AE切⊙O于D;(3分)
求证:AE切⊙O于D;(3分)
② 求证: ;(4分)
![]() ③ 如果⊙O的半径为
③ 如果⊙O的半径为![]() =2㎝,且
,求CD、OE的长;(4分)
=2㎝,且
,求CD、OE的长;(4分)
 |
8、 (11分)
已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;(3分)
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;(4分)
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由.(4分)