初三几何期末复习——直线与圆的位置关系(二)
一、与圆有关的角
| 图形 | 定义 | 定理 | 推论 |
|
| 顶点在圆心上的角 | 圆心角的度数等于它所对弧的度数 | |
|
| 顶点在圆上,并且两边都与圆相交角 | 1、一条弧所对的圆周角等于它所对的圆心角的一半 2、圆周角定理:圆周角的度数等于它所对弧的度数的一半 | 1、同弧或等弧所对的圆周角相等。 2、同圆或等圆中,相等的圆周角所对的弧也相等。 3、半圆(或直径)所对的圆周角是直角:900的圆周角所对的弦是直径。 |
|
| 顶点在圆上,并且一边和圆相交,另一边和圆相切的角叫弦切角 | 1、弦切角定理:弦切角等于它夹弧所对的圆周角。 2、弦切角的度数等于它所夹的弧的度数的一半 | 两个弦切角所夹的弧相等,两个弦切角也相等。 |
说明:在同圆或等圆中,圆心角相等![]() 弧相等
弧相等![]() 弦相等
弦相等![]() 弦心距相等,弧(劣)大
弦心距相等,弧(劣)大![]() 弦大
弦大![]() 弦心距小。
弦心距小。
二、添加辅助线的规律:
1、遇到直径时,一般要引直径所对的圆周角,将直径这一条件转化为直角条件。
2、遇到切线时,一般要引过切点的半径,以便利用切线的性质定理,或者连结过切点的弦,以便利用弦切角定理。
3、遇到过圆外一点的两条切线时,常常引这点到圆心的连线,以便利用切线长定理及推论。
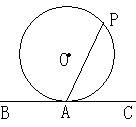
 1、(99辽宁)如图,PA分别切于⊙O于A、B,PA=5,
1、(99辽宁)如图,PA分别切于⊙O于A、B,PA=5,
在劣弧AB上取一点C,过C过作⊙O切线,分别交PA、PB
于D、E,则△PDE的周长等于____。
2、(98上海)一个圆的弦切角等于400,那么这个弦切角所夹
![]() 的弧所对的圆心角的度数是_____。
的弧所对的圆心角的度数是_____。
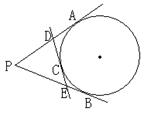
3、(99广东)如图(6),AB、AC是⊙O的两条切线,切点分别是B、C,D是优弧BC
上的点,已知∠BAC=500,则∠BDC=____度。

4、(96山西)如图(8),AB是⊙O直径,点D在AB的延长线上,BD=OB,若CD切⊙O于点C,则∠CAB的度数为_____,∠DCB=___,∠ECA的度数为_____
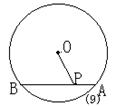
5、(97安徽)已知,如图(9),AB是⊙O的弦,P是AB上一点,AB=10cm,PA=4cm,OP=5cm,则⊙O的半径为____
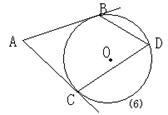
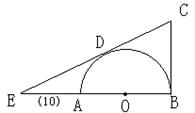
6、(98江苏)如图(10),AB是⊙O的直径,CB切⊙O于B,CD切⊙O于D,交BA的延长线于E,若EA=1,ED=2,则BC的长为________
7、圆外切等腰梯形上底长为4cm,圆的半径为3cm,那么这个梯形的腰长为 ( )
 A、
A、![]() B、
B、![]() C、7cm D、
C、7cm D、![]()
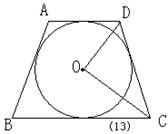
8、(2000吉林)如图(13),⊙O的外切梯形ABCD中,若以AD//BC,那么∠DOC度数为( )
A、700 B、900 C、600 D、450
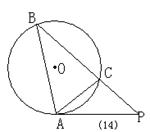
9、(2000哈尔滨)如图(14),经过⊙O上的点A的切线和弦BC延长线相交于点P,若∠CAP=400,∠ACP=1000,则∠BAC所对的弧的度数为( )
A、400 B、1000 C、1200 D、300
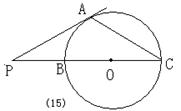
10、(2000辽宁)如图(15),PA为⊙O的切线,A为切点,割线PBC过圆心O,∠APC=300,OC=1cm,则PA的长为( )
 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、(99贵阳)已知等腰直角三角形外接圆半径为5,
则内切圆的半径为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
课后练习
 1、(98广西)PA、PB是⊙O切线,A、B切点,∠APB=780,点C是⊙O上异于A、B任一点,那么∠ACB=_____。
1、(98广西)PA、PB是⊙O切线,A、B切点,∠APB=780,点C是⊙O上异于A、B任一点,那么∠ACB=_____。
2、(96山西)若直角三角形斜边长为10cm,其内切圆半径
为2cm,则它的周长为_。
![]()
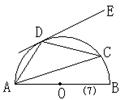
![]() 3、(98云南)如图(7),AB中⊙O直径,C、D是⊙O上的点,
3、(98云南)如图(7),AB中⊙O直径,C、D是⊙O上的点,
∠BAC=200,AD =DC,ED是⊙O的切线,则∠EDC的度数是____.
 4、(99天津)一圆中,两弦相交,一弦长为2a,且被交点平分,另一弦被分为1:4两部分,则另一弦长为_______
4、(99天津)一圆中,两弦相交,一弦长为2a,且被交点平分,另一弦被分为1:4两部分,则另一弦长为_______
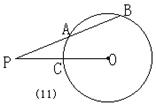
5、(99贵阳)如图(11),已知⊙O的割线PAB交⊙O于A和B,
PA=6cm,AB=8cm,PO交⊙O于点C,且PO=10cm,则⊙O的
半径为______
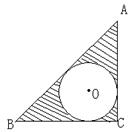 6、(98贵阳)如图,⊙O是Rt△ABC的内切圆,∠ACB=900,且AB=13,AC=12,则图中阴影部分的面积是( )
6、(98贵阳)如图,⊙O是Rt△ABC的内切圆,∠ACB=900,且AB=13,AC=12,则图中阴影部分的面积是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、(98天津)下列说法不正确的是( )
A、三角形的内心是三角形三条角平分线的交点
B、每条边都相等的圆内接四边形是正方形
C、垂直于半径的直线是圆的切线
D、有公共斜边的两个直角三角形有相同的外接圆
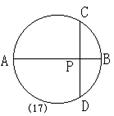 8、(2000四川)如图(17),AB是⊙O直径,弦CD⊥AB于点P,CD=10cm,AP:PB=5:21,那么⊙O的半径是( )
8、(2000四川)如图(17),AB是⊙O直径,弦CD⊥AB于点P,CD=10cm,AP:PB=5:21,那么⊙O的半径是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]() cm
cm
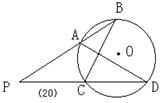 9、(98山西)如图(20),若直线PAB、PCD分别与⊙O交于点A、B、C、D,则下列各式中,相等关系成立的是( )
9、(98山西)如图(20),若直线PAB、PCD分别与⊙O交于点A、B、C、D,则下列各式中,相等关系成立的是( )
A、PA:PC=PB:PD
B、PA:PB=AC:BD
C、PA:PC=PD:PB
D、PB:PD=AD:BC
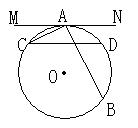 10、(98北京)如图,已知MN是⊙O切线,A为切点,MN平行于弦CD,弦AB交CD于E,
10、(98北京)如图,已知MN是⊙O切线,A为切点,MN平行于弦CD,弦AB交CD于E,
求证:AC2=AE·AB
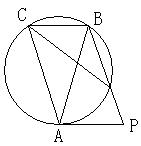 11、(99三明)已知:如图,圆内接△ABC中,AB=AC,PA是圆的切线,PB与相交圆相交于D,
11、(99三明)已知:如图,圆内接△ABC中,AB=AC,PA是圆的切线,PB与相交圆相交于D,
连结CD,求证:AC2=PB·CD