初三第三次模拟考试数学试卷
一、填空题（每小题3分，共36分）
1、计算：（+1）—（—2）=___________
2、方程3x=2—x的解是______________
3、函数
自变量x的取值范围是___________
4、△ABC中，AB=AC，∠A=80°，那么∠B=_______度
5、一次函数y=2x+b经过原点，则b=________
6、Rt△ABC中，∠C=90°，AB=6，
，则BC=________
7、
不等式组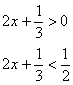 
的解是___________
8、以下命题中正确的有__________个
(1) 数据2、3、4、5的平均数是3.5
(2) 数据2、2、2、2的方差是0
(3) 某一事件成功的概率是
，那么这事件不成功的概率为
9、⊙O的两条弦AB、CD相交于P，CD=6，且PD是PA、PB 的比例中项，则PA·PB=________
10、如图，梯形ABCD中，AD∥BC，AD=3，BC=5，EF是梯
形的中位线，M是BF的中点，AM与EF相交于N，则
EN=__________
11、已知：a1+a2+a3+a4=(
+1)2，a1—a2+a3—a4=(—1)2，那么(a1+a3)2—(a2+a4)2=__________
12、游乐场转车的直径为36米，甲从地面A上车，50秒钟后发现自己的高度和三楼顶平（约9米高），如果转车匀速转动，估计转车转一圈需要的时间为_______分钟。
二、选择题（每小题3分，共24分）
13、函数
，当x=—2时，函数值是（ ）
A 
B —2 C 
D 2
14、a2—2a+1分解因式的结果是（ ）
A a(a—2)+1 B (a—1)2 C (a—2)2 D (a+1)(a—1)
15、光的速度约为3×105千米/秒，太阳光射到地球上需要的时间约是5×102秒，则地球与太阳的距离用科学记数法表示为（ ）
A 15×107千米 B 15×1010千米 C 1.5×108千米 D 0.15×109千米
16、⊙O的直径4，直线
与⊙O相切，那么圆心O到的距离为（
）
A 4 B 2 C 大于2且小于4 D 不能确定
17、如图，长方形AC′中，线段AC与D′B的大小关系是（ ）
A AC>D′B B AC=DB′ C AC<DB′ D 不能确定
18、下列命题中，是真命题的是（ ）
A 两个三角形某一对应边上的高的比是2：1，则它们的面积比是4：1
B 如果直角三角形两直角边分别为a、b，斜边上的高为h，那么
C 顺次连结等腰梯形四边中点所得的四边形是菱形
D 正三角形内切圆与外接圆面积之比为1：2
19、半径之比为1：3的两圆⊙O′和⊙O内切，⊙O的两条半径切⊙O′于AB，则∠AOB等于（ ）
A 30° B 45° C 60° D 90°
20、如图，正方形ABCD中，AB=1，Rt△PQR中∠Q=90°，PQ=RQ=1，P、Q、A、B在一条直线上，起始位置P与A重合，△PQR向右平移2个单位，在平移过程中，若PA=x，△PQR与正方形ABCD重叠的面积为y，则y与x的关系，可用以下图象表示（ ）
三、解答题
21、计算
22、先化简，再求值 
23、解方程组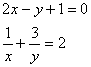 
24、作图题：画一个三角形A′B′C′，同时满足(1) △ABC∽△A′B′C′；
(2)S△A′B′C′=
△ABC
25、Rt△ABC中，∠C=90°，以AB为边作正方形ABEF，延长CB到D使BD=AC，连结AD、CF，求证：△ACF≌△BDA
26、船由A地向正东方向航线出发，航灯C在A的北偏东45°，船行7海里后，测得船距航灯C13海里，求C到航道的最短距离。
27、已知两种食物中的维生素A和B的含量及甲、乙食物的成本如下表：现将两种食物混合成100千克的混合食品，设混合食品中，甲、乙食物含量分别为x千克和y千克，如混合食品中要求维生素A不低于40000单位，B不低于28000单位。(1)求x的范围。(2)当甲、乙取多少千克时，符合题意的混合食品的成本最低，并求 最低成本价。
| 甲 | 乙 | |
| 维生素A（单位/千克） | 300 | 500 |
| 维生素B（单位/千克） | 700 | 100 |
| 成本（元/千克） | 5 | 4 |
28、二次函数y=x2—x+1，当x为自然数时，函数值为y，一次差是指函数值中，后一项与前一项的差，二次差是指一次差数据中，后一项与前一项的差。
(1)按要求填写下表。
(2)指出二次差的规律。
(3)是否对任意的二次函数y=ax2+bx+c都具有类似的规律，如果有请给出证明，如果没有，请举一个反例。
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6…… | |||||||||||||
| Y | 1 | 1 | 3 | 7 | 13 | …… | ||||||||||||||
| 一次差 | 0 | 2 | …… | |||||||||||||||||
| 二次差 | 2 | …… | ||||||||||||||||||
29、如图，AB是半圆O的直径，AB=5，C是半圆上一点，
，E是AC上一点，BE交AC于D。
(1) 若D是AC的中点，求BE的长。
(2)
AC上是否存在点E，使得
，若不存在说明理由；若存在求EC的长。