初三(上)数学期末试题
一、填空题(共20分,每小题2分)
1、在直角坐标系中,点P(-5,3)在第 象限。
2、x1、x2是方程x2-2x-6=0的两根,那么x1+x2= ,x1·x2= 。
3、点P(3,5)关于x轴对称的点的坐标是 。
4、到相交两直线距离相等的点的轨迹是 。
5、已知sin66°=0.9135,那么cos24°= 。
6、反比例函数y=-2/x的图象位于第 象限。
7、求值:cos245°+tan60°cos30°= 。
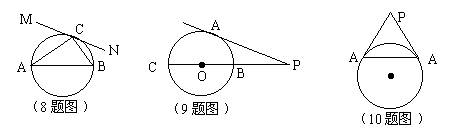
8、如图,直线MN与圆相切于点C,AB为直径,如果∠A=40°,那么∠ACM= 。
9、如图,PA切⊙O于点A,PBC交圆O于点B、C,如果PA=6,PB=PC,那么PC= 。
 10、如图,PA、PB是⊙O的切线,A、B是切点,且△APB是等边三角形,如果PA的长为a,那么⊙O的半径长为 。
10、如图,PA、PB是⊙O的切线,A、B是切点,且△APB是等边三角形,如果PA的长为a,那么⊙O的半径长为 。
二、选择题(共10分,每小题2分)
1、一元二次方程2x2-x-3=0的一次项系数是( )
A、2 x2 B、-1 C、-3 D、-x
2、一元二次方程x2-5x-1=0的根的情况是( )
A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、有一个实数根
3、函数y=![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A、x>3 B、x≥3 C、x<3 D、x≤3
4、如果正比例函数y=kx(k≠0),y随x的增大而减小,那么相应的一次函数y=kx+b(b<0)经过( )
A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限
5、如图,AB为⊙O的直径,弦AC、BD相交于点P,那么CD/AB等于( )
A、sin∠BPC B、cos∠BPC C、tan∠BPC D、cot∠BPC
三、(共21分,每小题7分)
1、 已知反比例函数y=k/x(k≠0)的图像经过点(4,3),求当x=6时,y的值。
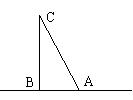
2、 如图,点A在距离铁塔塔底20米远的地面上,在A处测得塔顶的仰角为62°30′,求铁塔的高BC(精确到0.1米,以下可供选择的数据为:sin62°30′=0.8870、
cos62°30′=0.4617、tan62°30′=1.921、cot62°30′=0.5206)
3、
解方程组: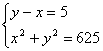
四、(共24分,每小题6分)
1、
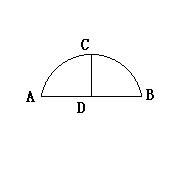 某地野生动物园的河上要建筑一圆形的拱桥,设计上要求拱桥的跨度为30米,拱高(弧的中点到弦的距离)为5米,为计划圆弧拱桥所需材料,必须先求得圆弧所在圆的半径,请你运用所学知识,求出这条半径为多少?(如图,为拱桥的示意图,用弧AB表示拱桥,CD为拱高,AB为拱桥的跨度)
某地野生动物园的河上要建筑一圆形的拱桥,设计上要求拱桥的跨度为30米,拱高(弧的中点到弦的距离)为5米,为计划圆弧拱桥所需材料,必须先求得圆弧所在圆的半径,请你运用所学知识,求出这条半径为多少?(如图,为拱桥的示意图,用弧AB表示拱桥,CD为拱高,AB为拱桥的跨度)
2、
用换元法解方程:![]()
3、已知二次函数y=-![]() ;(1)通过配方法将函数写成y=a(x-h)2+k的形式;
;(1)通过配方法将函数写成y=a(x-h)2+k的形式;
(2)写出这个函数图象的顶点坐标和对称轴及开口方向;(3)求函数图象与坐标轴的交点坐标。
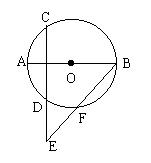 4、已知:如图,点E在与直径AB垂直的弦CD的延长线上,连结BE,交⊙O于点F。
4、已知:如图,点E在与直径AB垂直的弦CD的延长线上,连结BE,交⊙O于点F。
求证:BC2=BE·BF。
五、(共12分,每小题6分)
1、 某钢铁厂去年8月份的钢产量为5000吨,9月份的产量下降了10%,工厂及时采取措施后,产量持续上升,11月份的产量上升到6480吨,问10、11月份两个月平均每月增长的百分数是多少?
2、
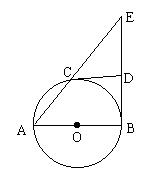 已知:如图,AB是⊙O的直径,点E在⊙O外,AE交⊙O于点C,CD是⊙O的切线,交BE于点D,C为切点,且DE=DB。求证:BE是⊙O的切线。
已知:如图,AB是⊙O的直径,点E在⊙O外,AE交⊙O于点C,CD是⊙O的切线,交BE于点D,C为切点,且DE=DB。求证:BE是⊙O的切线。
六、(共6分)甲种糖果的进价为每千克6元,乙种糖果的进价为每千克10元,某商店将甲、乙两种糖果混合(搅拌均匀)销售,经过市场调查,发现在混合的糖果中,当加入乙种糖果的重量不少于甲种糖果重量的2倍时,最好销售,如按这种比例混合搅拌制15千克糖果;
(1)设混合糖果中有甲种糖果x千克,拌制的15千克混合糖果中,甲、乙两种糖果的进价共为y元,写出y与x的函数关系式;
(2)求出(1)中函数的自变量x的取值范围;
(3)商家在拌制这15千克混合糖果时,甲、乙两种糖果各取多少千克,获利最大?
七、(共7分)
如图,直线AC交x轴的正半轴于点A,交y轴的正半轴于点C,以AC为直径的⊙F过原点O,点在B 第一象限,且在⊙F上,BC∥x轴,点D在第四象限,且在⊙F上,CD交x轴于点E,弧AB=弧AD,连结AB、AD,tan∠ECO=3/4,CE=10。
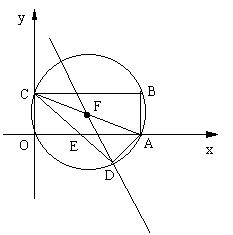 (1)求OE、OC的长;(2)求点D的坐标;(3)判断点(16,-18)是否在过D、F两点的直线上,并说明理由。
(1)求OE、OC的长;(2)求点D的坐标;(3)判断点(16,-18)是否在过D、F两点的直线上,并说明理由。