初三数学综合训练一
班级 姓名 记分
一、选择题：（每题3分，共10分）
1、在直角坐标系中（0，5）在（ ）
A、x轴上 B、y轴上 C、 第一象限 D、 第四象限
2、函数y=
中自变量的取值范围是（ ）
A、x≥2 B、x≤2 C、x≠2 D、x>2
3、函数y=
中，自变量x的取值范围是（ ）
A、x>3 B、x≥3 C、x<3 D、x≤3
4、如果正比例函数y=kx（k≠0），y随x的增大而减小，那么相应的一次函数y=kx+b
（b<0）经过（ ）
A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限
5、如图，AB为⊙O的直径，弦AC、BD相交于点P，那么CD/AB等于（ ）
A、sin∠BPC B、cos∠BPC C、tan∠BPC D、cot∠BPC
6、抛物线y=x2-bx+8的顶点在x轴上，b的值一定为 ( )
(A) 4 (B) -4 (C)
2或-2 (D) 4
或-4
7、设y=x2+x，则方程x2+x+1=
可变形为（ ）
A、y2－y－2=0 B、y2+y+2=0 C、y2+y－2=0 D、y2－y+2=0
8．某同学骑自行车上学，开始以正常速度匀速行驶。但行至中途因车出了毛 病，只好停下修车，车修好后，因怕耽误上课他比修车前加快了骑车速度 继续匀速行驶。下面是行驶路程S关于行驶时间t的函数图象（见图），那 么符合这个同学行驶情况的图象大致是（ ）
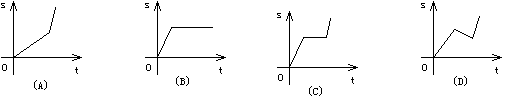
9、下列式子正确的是（ ）
A、sin66°>sin68° B、tan66°>tan68°
C、cos66°>cos68° D、cot66°<cot68°
10、圆内接四边形ABCD中，∠B:∠C:∠D=5:4:1, 则∠A的度数是 。
A：50° B：60° C：70° D：80°
二、填空题：（每题3分，共30分）
1、设路程为s（千米），速度为v（千米/小时），时间为（t小时），关系式t=50/v中，变 量是 ，常量是 。
2、在几何图形中， 既是轴对称又是中心对称图。（只填写满足条件的图形一个）。
3、函数y=2x－5，当x=2时，函数值是 。
4、一次函数y=(m2－4)x+(1－m)和y=(m－1)x+m2－3的图象与y轴分别交于点P和点Q，若 点P和点Q关于x轴对称，则m 。
5、点P（3，5）关于x轴对称的点的坐标是 。
6、到相交两直线距离相等的点的轨迹是 。
7、已知sin66°=0.9135，那么cos24°= 。
8、圆外切等腰梯形中位线长为10，则它的周长为 。
9、半径分别为4厘米和1厘米的相外切的两圆的外公切线长是 厘米。
10、两个正五边形的周长分别为15和20，则它们半径的比为 。
三、解答题：（每小题10分）
1、甲、乙两地相距600km，快车匀速走完全程需10小时，慢车匀速走完全程需15小时， 两车分别从甲、乙两地同时相向而行，求出发到相遇，两车的距离y（km）与行驶时 间x（h）之间的函数关系式，指出自变量x的取值范围。
2、某车间有20名工人，每人每天加工甲种零件5个或乙种零件4个。在这20名工人中，派x 人加工甲种零件，其余的加工乙种零件。已知每加工一个甲种零件可获利16元，每加 工一个乙种零件可获利24元。
（1）写出此车间每天所获利润y（元）与x（人）之间的函数关系式。
（2）若要使车间每天获利不低于1800元，问至少要派多少工人加工乙种零件。
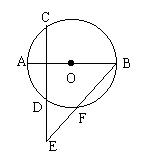
3、已知：如图，点E在与直径AB垂直的弦CD的延长线上，连结BE，交⊙O于点F。
求证：BC2=BE·BF。
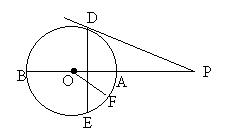
４、已知：如图AB是⊙O的直径，弦DE⊥AB，垂足为C，过点D作⊙O的切线交BA的延长 线于点P，tan∠P=
/15，PO=16。
（1）求⊙O的半径；
（2）求OC的长；
（3）如果 F为弧AE的中点，求cos∠AOF的值。
