初三数学综合训练二
班级______姓名_________得分________
一、填空题(共30分,每小题3分)
1、x1、x2是方程x2-2x-6=0的两根,那么x1+x2= ,x1·x2= 。
2、点P(3,5)关于x轴对称的点的坐标是 。
3、 知a=2.5㎝,b=40㎝,那么a和b的比例中项d=______.
4、
长线段AB到C,使BC=![]() AB,那么AC:AB=________.
AB,那么AC:AB=________.
5、圆内接四边形ABCD中,如果∠B=60°,那么∠D= 度。
6、函数y=3x-2,y随x的 而增大。
7、⊙O中弦AB=8cm,弦心距为3cm,那么⊙O的半径为 ㎝。
8、函数![]() 中自变量
中自变量![]() 的取值范围是____________________.
的取值范围是____________________.
9.若反比例函数y =![]() 的图象在一、三象限,则一次函数y=kx+1的图象
的图象在一、三象限,则一次函数y=kx+1的图象
不过第 象限。
10、 梯形ABCD的腰BA和CD的延长线交于E,EB:AB=8:5 ,
DC=6㎝,则ED=_______㎝.
二、选择题(共30分,每小题3分)
1、一元二次方程2x2-x-3=0的一次项系数是( )
A、2 x2 B、-1 C、-3 D、-x
2、一元二次方程x2-5x-1=0的根的情况是( )
A、无实数根 B、有两个相等的实数根
C、有两个不相等的实数根 D、有一个实数根
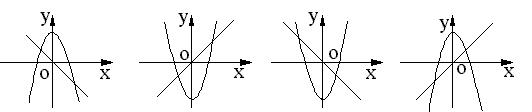
3.在直角坐标系中,函数y= -3x与y=x2-1的图象大致是( )
 A.
B.
C.
D.
A.
B.
C.
D.
4.如果两圆有且只有一条公切线,那么两圆的位置关系是( )
A. 外切 B、 相交 C、 内切 D、 内含
5、同圆的内接正三角形与正六边形的边长之比为( )。
(A) 1:2 (B) 1:1 (C)√3:1 (D) 2:1
6、知![]() =k, 那么k=( )
=k, 那么k=( )
A.![]() B.-1 C.-1,
B.-1 C.-1, ![]() D.0
D.0
7、 知CD是Rt△ABC斜边AB上的高,在这组图形中,相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
8、点P(2,3)关于y轴对称的点的坐标是( )
A、(2,-3) B、(-2,3) C、(-2,-3) D、(2,3)
9、下列各式中错误的是( )
A、sin30°=cos60° B、sin45°=cos45° C、cos25°=sin65° D、cos25°=sin25°
10、一次函数y=6x+8的图象经过( )
A、一、三、四象限 B、二、三、四象限
C、一、二、三、象限 D、一、二、四象限
三、解答题:
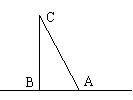
1、 (7分)如图,点A在距离铁塔塔底20米远的地面上,在A处测得塔顶的仰角为62°30′,求铁塔的高BC(精确到0.1米,以下可供选择的数据为:sin62°30′=0.8870、
cos62°30′=0.4617、tan62°30′=1.921、cot62°30′=0.5206)
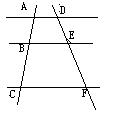
2、(6分) 如图,AD∥BE∥CF, AB=3, AC=8, DE=5, 求DF的长.
3、
(6分)方程组: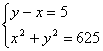
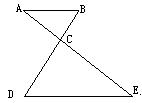 4. (7分)如图,AB∥DE,AC=4,BD=9,CD=6.
4. (7分)如图,AB∥DE,AC=4,BD=9,CD=6.
求CE的长.
5、(7分)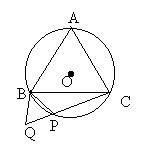 已知:如图,△ABC是⊙O的内接等边三角形,点P在弧BC上,延长CP到Q,使PQ=PB;求证:(1)△PBQ是等边三角形;
已知:如图,△ABC是⊙O的内接等边三角形,点P在弧BC上,延长CP到Q,使PQ=PB;求证:(1)△PBQ是等边三角形;
(2)CQ=AP。
6、
(7分)在直角坐标系xoy中,二次函数图象的顶点坐标为C(4,![]() ),且在x轴上截得的线段长为6。
),且在x轴上截得的线段长为6。
a) 求二次函数的解析式。
b)
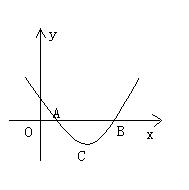 在x轴上方的抛物线上,是否存在点Q,使得以Q、A、B三点为顶点的三角形与△ABC相似;如果存在,请求出Q点的坐标;如果不存在,请说明理由。
在x轴上方的抛物线上,是否存在点Q,使得以Q、A、B三点为顶点的三角形与△ABC相似;如果存在,请求出Q点的坐标;如果不存在,请说明理由。