 初三数学综合试题
初三数学综合试题
一、填空题:(每小题3分,共30分)
1、计算:-3 - ![]() -3
-3![]() = 。
= 。
2、分解因式:![]() 。
。
3、若![]() 是方程
是方程![]() ,则a = 。
,则a = 。
4、函数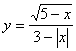 中自变量取值范围是 。
中自变量取值范围是 。
5、已知关于![]() 的一元二次方程
的一元二次方程![]() 的两根为3和-1,则
的两根为3和-1,则![]() 。
。
6、已知样本数据:98,99,100,101,102 。则它们的标准差是 。
7、已知二次函数![]() 中,当
中,当![]() ,y <0,则其对称轴是 。
,y <0,则其对称轴是 。
 8、若
8、若![]() ,则
,则![]() 。
。
9、线段AB=2cm,P是AB的黄金分割点,且PA>PB,则PB= 。
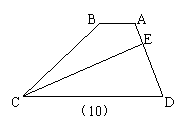
10、如图,在梯形ABCD中,AB∥CD,CE平分∠BCD,且CE⊥AD于E,若DE=2AE,![]() ,则
,则![]() 。
。
二、 选择题(每小题3分,共30分)
1、
当a为实数时,![]() ,则实数a在数轴上对应的点在( )
,则实数a在数轴上对应的点在( )
A、原点的右侧;B、原点的左侧;C、原点或原点右侧;D、原点或原点的左侧。
2、下列方程中有实数解的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
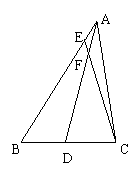 3、已知四个函数(1)y = - x (2)
3、已知四个函数(1)y = - x (2)![]() (3)
(3)![]() (4)
(4)![]() 其中y随x 的增大而增大的函数有( )
其中y随x 的增大而增大的函数有( )
A、1个 B、2个 C、3个 D、4个
![]()
4、已知ΔABC中,∠C=90°,CD是AB边上的高,则CD∶CB等于( )
A、SinA B、CosA C 、tgA D、ctgA
5、ΔABC中,AD是BC边上的中线,F是AD上一点,且AF∶FD =1∶5,连结CF并延长交AB于E,则AE∶EB等于( )
A、1∶6 B、1∶8、 C、1∶9 D、1∶10
6、已知抛物线![]() 的图象开口向上,对称轴为
的图象开口向上,对称轴为![]()
,若![]() ,
,![]() ,
,![]() 时,的函数值分别为y1 , y2 ,y3 ,则y1 ,y2 , y3的大小关系为 ( )
时,的函数值分别为y1 , y2 ,y3 ,则y1 ,y2 , y3的大小关系为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、把50个数据分成6组,前4个组的频率分别为2,4,11,20,第五组的频率为0.20,则第六组的频率是( )
A、0.06 B、0.1 C、0.15 D、0.3
8、一元二次方程![]() 的两根和为
的两根和为![]() ,则两根之积为(
)
,则两根之积为(
)
A、2 B、-2 C、 - 6或2 D、6或 – 2
 9、销售某种商品,如价格上涨 x ,则销售量就要减小0.8x ,要使销售所得资金额最大,则 x 的值为( )
9、销售某种商品,如价格上涨 x ,则销售量就要减小0.8x ,要使销售所得资金额最大,则 x 的值为( )
A![]() B、
B、![]() C、
C、![]() D、
D、![]()
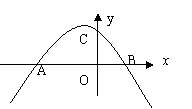
10、如图抛物线![]() 与 x 轴相交于A、B两点,与y轴交于C点,若OB=OC=0.5OA,则b的值为( )
与 x 轴相交于A、B两点,与y轴交于C点,若OB=OC=0.5OA,则b的值为( )
A、0.5 B、- 0.5 C、-1 D、 -2
三、![]() 解答题
解答题
1、 计算(本题5分)
2、(本题5分)已知![]() ,
,![]() 。求
。求![]() 的值。
的值。
3、(本题5分)解方程![]()
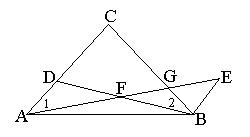
4、(本题6分)如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于F、G,且∠1=∠2 。(1)求证:ΔFAD≌ΔFEB;(2)求证:FG×BE=BG×FD
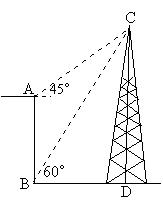
5、(本题6分)一暸望台AB高20m ,从暸望台底部B测得对面塔顶C的仰角为60°,从暸望台顶底A测得塔顶C的仰角为
45°。已知暸望台与塔CD地势高低相同。求塔高CD的长。
 6、(本题6分)抛物线
6、(本题6分)抛物线![]() 经过点(1,0)、(5,0),(4,3)。(1)求抛物线的解析式。(2)若抛物线顶点的横坐标,纵坐标分别是方程
经过点(1,0)、(5,0),(4,3)。(1)求抛物线的解析式。(2)若抛物线顶点的横坐标,纵坐标分别是方程![]() 的两个根。求:m ,n的值。
的两个根。求:m ,n的值。
![]()
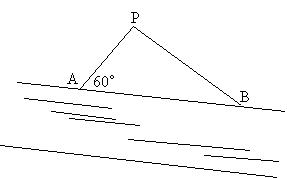
7、(本题9分)如图,有块直角三角形菜地,分配给张、王、李三家农户耕种。已知张、王、李三家人口分别为2人、4人、6人,菜地分配办法按人口比例,并要求每户土地均有一部分紧靠水渠AB,P点处是三家合用的肥料仓库,P点必须是三家地的交界处。已知RtΔPAB的∠P=90°,PA=20m ,∠PAB=60°。
(1) 计算出每家应分配的菜地面积(4分)
(2) 用尺规在图中作出各家菜地的分界线。(保留作图痕迹,不写作法,标出名称)(5分)
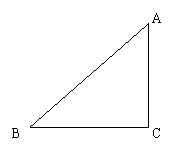
8、(本题8分)如图ΔABC中,∠A= 45°,AB+AC = 8cm ,设AC= x cm ,
ΔABC的面积为 y cm2 。(1)求 y 关于 x 的函数关系式和自变量 x 的取值范围;
(3)
 当x为何值,ΔABC的面积为最大?最大面积为多少?
当x为何值,ΔABC的面积为最大?最大面积为多少?
9、(本题10分)如图,抛物线![]() 与
与![]() 轴交点为A 、B(A在B左侧),与
轴交点为A 、B(A在B左侧),与![]() 轴交点为C ,顶点为P,连结PC并延长交
轴交点为C ,顶点为P,连结PC并延长交![]() 轴于点N。
轴于点N。
(1)
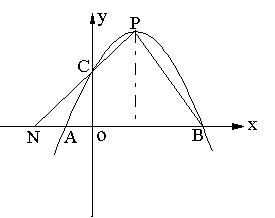 求经过P、C两点的直线解式。(3分)
求经过P、C两点的直线解式。(3分)
(2) 求ΔNPB的面积。(3分)
(3) 求Sin∠BPN的值。(4分)