初三数学综合练习

　　　　  初三数学综合练习 　　 姓名________　

一、填空题（2′×3+3′×18＝60′）

1.　　　 –7的倒数是______；－2.8的绝对值是______；的算术平方根是____.

2.　　　 大量事实表明，治理垃圾污染刻不容缓，据统计，某市每天的生活垃圾达2.09万吨.如果一年按365天计算，那么该市一年的垃圾大约为　　　　吨（用科学计数法表示，结果保留三个有效数字）.

3.　　　 把4x⁴y²-5x²y²-9y²分解因式得　　_____. 如果4a-3b=0,那么　　　的值为　　.

4.　　　 如果a+=2,那么a的取值范围是___________.

5.　　　　　　　 已知方程x²+4x-2k=0的一根为α，比另一根β小4，则α、β、k的值分别为　　　　.

6.　　　 在同一直角坐标系中，对于函数①y=-x-1,②y=x+1;③y=-x+1;④y=-2(x+1)的图象，其中交点在y轴上的是　　　　，不经过第四象限的是　　　　（填序号）.

7.　　　 如果顺次连结四边形ABCD四边中点得四边形EFGH,要使EFGH是菱形，应添加的条件是　　　　______.

8.　　　 抛物线y=x²-2x+a²的顶点在直线y=2上，则a的值是　　　　，当x　　　　　　　  　　　　__________时，y随x的增大而增大.

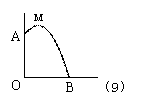
9.　　　　　　　 某撞建筑物，从10米高的窗口A用水管向外喷水，喷水的水流呈抛物线状.如果抛物线的最高点M离墙1米，离地面米， 则水流落地点B离墙的距离OB＝　　　　.

10.　 用一个直径为6cm的半圆纸片做成一个圆锥的侧面，则此圆锥的底面直径为　　　　.

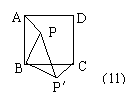
　　11.如图，正方形ABCD内一点P，将ΔABP绕点B顺时针旋转能与ΔCBP′重合，若BP=3，则PP′=　　　　.

　　　　　　　　　　　　　　　

　　

　　

　　

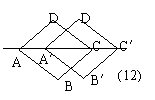
　　12.把菱形ABCD沿着对角线AC的方向移动到菱形A′B′C′D′的位置，它们的重叠部分的面积是菱形ABCD的面积的一半，若AC＝，则菱形移动的距离AA′是　　　　.

　  13. 下列每个图是由若干盆花组成的形如三角形的图案，每边（包括两个顶点）有n（n>1）盆花，每个图案的花盆的总数是s.

n=2,s= 3　 n=3,s=6　 n=4,s=9

　　　　　　　　　　　　　　　  按此规律推断，s与n的关系式为　　　　.

14.抛物线经过直线y=x+3与双曲线y= 的一个交点，且以另一交点为顶点，此抛物线的解析式是　　　　　　　  _______.

15.在⊙O中，弦AB是圆内接正三角形的一边，弦AC是同圆内接正六边形的一边，则∠BAC＝　　　　.

16.一种商品，每件进价a元，将进价增加25％定出零售价格，后因仓库积压，决定降价，按零售价格的92％出售，那么每件还能盈利　　　　元.

二、计算或解方程（4′×2＝8′）

　 1.　　　　　　 2. x²+3x－　　　　+1=0

三、解答题（6′×4+8′＝32′）

1.　　　 2.如图：在梯形ABCD中，AD∥BC，AB＝CD，BD＝，∠DBC＝30°，∠BDC＝90°，求梯形ABCD的面积.

 

 

 

2.　　　  如图：ΔABC是等边三角形，⊙O与AC相切于A点，与BC相交于E点，与AB的延长线相交于D点，已知AC＝10cm，CE＝4cm，求 BD的长.

 

 

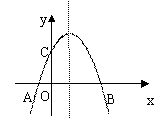3.如图：抛物线y＝ax²＋bx＋c与x轴相交于A、B两点（A、B分别在原点左、右两侧）与y轴正半轴交于点C，OA∶OB∶OC＝1∶4∶4，ΔABC的面积为40.⑴求A、B、C三点的坐标；⑵求抛物线的解析式.

4.甲、乙两台机床同时加工直径为100mm的零件，为了检验产品的质量，从产品中各随机抽出6件进行测量，测得数据如下；（单位；mm）

甲机床：99　100　98  100　100　103 ；乙机床：99　100　102  99　100　100

⑴分别计算上述两组数据的平均数及方差（写出过程）；⑵根据⑴的计算结果，说明哪一台机床加工这种零件更符合要求.

5.若抛物线y＝ax²＋bx＋c过y轴上的一点C(0,2),且与x轴只有一个交点A，又b＋2ac＝0，另有直线y＝x＋m过A点且与抛物线相交于B点，与y轴相交于P点.⑴求直线与抛物线的解析式，并画草图；⑵连结AC、BC，试判断ΔABC的形状；⑶以BC为直径作⊙M，过P作直线PN切⊙M于N，并与过点B且平行于y轴的直线交于Q，求PN、PQ的值.