初三数学综合练习（三）

初三数学综合练习（三）

姓名　　　　班级　　　学号

一、填空题（2×16=32分）

1、如果a、b互为相反数，m、n互为倒数，k的绝对值为2，那么100a+99b+mnb+k²的值为　　　　　 。

2、如果0.=3.14×10ⁿ，那么n=　　　　。

3、25的平方根是　　 ，的算术平方根是　　　　 。

4、设a、b、c为△ABC三边的长，那么+a+b-c=　　　　 。

5、能使不等式成立的x最大整数值是　　　　。

6、如果a、b、c表示△ABC的三边，且方程有两个相等的实数根，那么这个三角形是　　　　　 三角形。

7、如果关于x的方程x²－2(m+1)x+m²－2=0的两个根之和等于两根之积的相反数，那么m=　　　　。

8、如果，那么　　　　　 。

9、分母有理化得　　　　 。

10、菱形ABCD的对角线AC=24，BD=10，那么等于　　　　 。

11、样本2、4、3、6、5、8、7、3的平均数，中位数和众数分别是　　　　　 。

12、在Rt△ABC中，∠C=90°，BC=4，sinA=2/3，那么AB=　　　　。

13、已知矩形ABCD的一边AB=10cm，另一边AD=3cm，如果以直线AB为轴旋转一周，那么所得的圆柱的侧面积是　　　　  cm²（不取近似值）

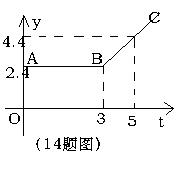
14如图中的折线ABC，为甲地向乙地打长途电话费y（元）与通话时间t（分钟）之间的函数关系的图象，当t≥3时，该图象的解析式为　　　　　  ；从图象上可知，通话2分钟需付电话费　　　元；通话7分钟需付电话费　　　　 元。

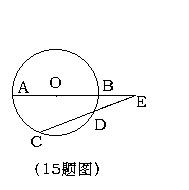
15如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E，已知AB=2DE，∠E=18°，那么∠AOC=　　　　 度。

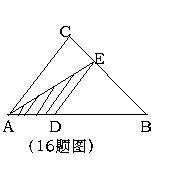16、如图△ABC中，CE∶EB=1∶2，DE∥AC，如果△ABC的面积为S，那么△ADE的面积为　　　　　  。

　　　　　　　　　　　　　　　　　　　

二、选择（2×10=20分）

1、下列计算正确的是（　　）

A、(－x) ³÷(－x) ²=x　　　　　　　　　　　　　　　　　 B、(2a+b) ³÷(2a+b)=(2a+b) ²　　　

C、　　　　 D、

2、下列各式中正确的是（　　 ）

A、　 　　　　B、　

C、　　　　 D、　

3、下列等式不成立的是（　　）

A、　 B、　 C、　 D、

4、如果a、b、c是实数，当a>b时，那么必有（　　　 ）

A、ac>bc　　 B、ac<bc　　　　 C、ac²>bc²　　　D、ac²≥bc²

5、下列三角形不是直角三角形的是（　　  ）

A、三角形的三边分别是5、12、13

B、三角形中有一边上的中线等于这边的一半

C、三角形的三内角之比是1∶2∶3

D、三角形的三边之比为1∶∶

6、在△ABC中，∠C=90°，sinA=/2，cosB的值是（　　）

A、1/2　　B、/2　　C、/2　　 D、1

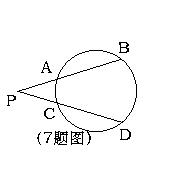
7、如图，PAB和PCD是圆的两条割线，交圆于点A、B和点C、D，如果PA=5，AB=7，CD=11，那么AC∶BD等于（　　 ）

A、1∶3　　　　 B、5∶12　　　C、5∶7　　　 D、5∶11

8、已知a·b<0，点P(a，b)在反比例函数y=a/x的图象上，那么直线y=ax+b不经过的象限为（　 　 ）

A、第一象限　　 B、第二象限　　　　C、第三象限　　　　 D、第四象限

9、已知正比例函数y₁=ax，反比例函数y₂=b/x在同一坐标系中该两个函数的图象没的交点，那么a与b的关系是（　　）

A、同号　　  B、异号　　　C、互为倒数　　　D、互为相反数

10、一个扇形的弧长是20πcm，面积是240πcm²，那么扇形的半径是（　　　）

A、6cm　　　 B、12cm　　　　C、24cm　　　 D、2cm

三、（4×3=12分）

1、　计算

2、　计算

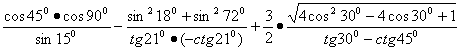
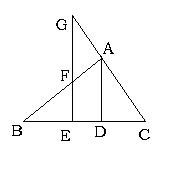3、　已知：如图△ABC中，AD⊥BC，垂足为D，E为BD上一点，EG∥AD，分别交AB和CA的延长线于点F、G。∠AFG=∠G。（1）求证△ABD≌△ACD；

（2）如果∠B=40°，求∠G和∠FAG的大小。

四、（4×2=8分）

1、　解方程

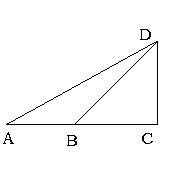2、　如图，某人要测一建筑物CD的高度，他在地面A处测得建筑物顶端D的仰角为30°，沿AC方向前进10米到达点B处，测得建筑物的顶端D的仰角为45°，求建筑物的高度（精确到0.1米，）

五、（5×2=10分）

1、某工程由甲、乙两队合做6天完成，厂家需付甲、乙两队共8700元；乙、丙两队合做10天完成，厂家需付乙、丙两队共9500元；甲、丙两队合做5天完成全部工程的2/3，厂家需付甲、丙两队共5500元。

（1）求甲、乙、丙各队单独完成全部工程各需多少天？

（2）如果工期要求不超过15天完成全部工程，问可由哪队单独完成此项工程花钱最少？说明理由。

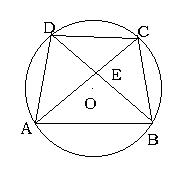2、已知：如图，⊙O的内接四边形ABCD中AD=CD，AC交BD于点E，求证（1）；（2）AD·CD－AE·EC=DE²

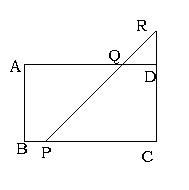六、（6分）已知：如图，矩形ABCD中，AB=4，BC=7，P 是BC边上与点B不重合的动点，过点P的直线交CD的延长线于点R，交AD于点Q（Q与D不重合）且∠RPC=45°，设BP=x，梯形ABPQ的面积为y，求y与x之间的函数关系，并求出自变量x的取值范围。

七、（6分）如图，双曲线y=5/x在第一象限的一支上有一点C（1，5）过点C的直线

y=－kx+b(k>0)与x轴交于点A(a，0)

（1）求点A的横坐标a与k之间的函数关系式（不写自变量取值范围）；

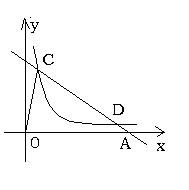（2）当该直线与双曲线在第一象限的另一交点D的横坐标是9时，求△COA的面积。

八、（6分）已知：如图，⊙O和⊙O′相交于点A、B，过点A作⊙O′的切线交⊙O于点C，过点B作两圆的割线分别交⊙O、⊙O′于点E、F，EF与AC相交于点P

（1）求证：PA·PE=PC·PF　 （2）PE²/PC²=PF/PB

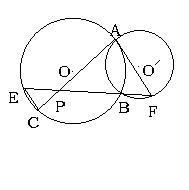（3）当⊙O与⊙O′为等圆，且PC∶CE∶EP=3∶4∶5时，△ECP与△EAP的面积的比值。