初三数学专题（六）—圆二
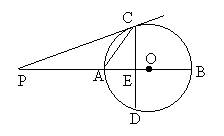1、如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，且PC2=PE·PO。（1）求证：PC是⊙O的切线。（2）若OE∶EA=1∶2，PA=6，求⊙O的半径。
（3）求sin∠PCA的值。
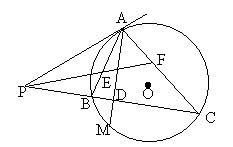
2、如图，PA为⊙O的切线，A为切点，PBC为割线，∠APC平分线PF交AC于点F，交AB于点E。（1）求证：AE=AF；（2）若PB∶PA=1∶2，M是弧BC上的一点，AM交BC于D，且PD=PC，试确定M点在弧BC上的位置，并证明你的结论。
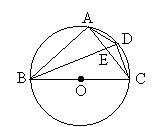
3、已知：如图，BC为圆的直径，O为圆心。D是弧AC的中点，四边形ABCD的对角线AC、BD交于点E。（1）求证△ABE∽△DBC；（2）已知BC=5/2，CD=
/2，求sin∠AEB的值。（3）在（2）的条件下，求弦AB的长。
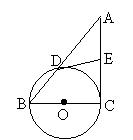
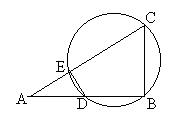
4、如图，BC是⊙O的直径，A是弦BD延长线上一点，切线DE平分AC于E。
求证（1）AC是⊙O的切线；（2）若AD∶DB=3∶2，AC=15，求⊙O的直径。
5、如图，在△ABC中，AB=4，BC=3，∠B=90°，点D在AB上运动，但与A、B不重合，过B、C、D三点的圆交AC于E，连结DE。（1）设AD=x，CE=y，求y与x之间的函数关系式，并指出自变量x的取值范围；（2）当AD长为关于x的方程2x2+（4m+1）x+2m=0的一个整数根时，求m的值。
6、如图，△ABC内接于⊙O，BC=4，S△ABC=6
，∠B为锐角，且关于x的方程x2－4xcosB+1=0有两个相等的实数根。D是劣弧AC上任一点（点D不与点A、C重合），DE平分∠ADC，交⊙O于点E，交AC于点F（1）求∠B的度数；（2）求CE的长；
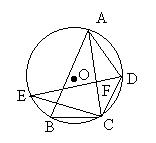（3）求证：DA、DC的长是方程y2－DE·y+DE·DF=0的两个实数根。