初三数学月考(二)
班级 姓名 学号
一、填空题(2×13=26分)
1、方程x2+kx+2=0的一个根是1,那么k= 。
2、点P(5,—3)关于原点对称的点的坐标是 ,点P到原点的距离是 。
3、点(3,—2)到x轴的距离是 ,到y轴的距离是 。
4、函数![]() 的自变量x的取值范围是
。
的自变量x的取值范围是
。
5、配方:x2+8x+9=(x+ )2+( )
6、在RtΔABC中,∠C=90°,cosA=1/5,那么sin(90°—A)= 。
7、ΔABC中,如果∠A=90°,a、b、c分别是∠A、∠B、∠C的对边,则cosB·cotC= 。
8、已知y与x2成正比例,当x= —2时,y=12,则y与x之间的函数关系式为 。
9、在函数y=![]() 中,y随x的减小而
。
中,y随x的减小而
。
10、一次函数y=2x+m的图象不经过第二象限,则实数m的取值范围是 。
11、若一元二次方程x2-12x+m=0的两根之比为1∶5,则m= 。
12、已知等腰三角形的周长为50cm,设腰长为xcm,底边长为ycm,那么y与x之间的函数关系式为 ,自变量x取值范围是 。
13、已知:α、β为锐角,且(2cosβ![]() )2+2sinα-1=0,则α= 度,β= 度。
)2+2sinα-1=0,则α= 度,β= 度。
二、选择题(2×10=20分)
1、一元二次方程3x2-5x-4=0的两根是x1、x2,则的x1·x2值是( )
A、4/3 B、—4/3 C、5/3 D、—5/3
2、在平面直角坐标系中,点(3,—2)所在象限是( )
A、一象限 B、二象限 C、三象限 D、四象限
3、方程x2-2x+3=0的根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实数根
C、没有实数根 D、有两个正实数根
4、把2x2-4x-5分解因式,结果正确的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、下列判断正确的是( )
A、RtΔABC中,sinB=2/5,如果三角形各边都扩大2倍,则sinB=4/5
B、![]() =sin45°-1
C、sin75°=sin30°+sin45°
=sin45°-1
C、sin75°=sin30°+sin45°
D、RtΔABC中,如果cosA=3/5,那么sinA=4/5。
6、如果一次函数y=kx+b的图象经过第一、三、四象限,且b=3,k=2b,则此一次函数的解析式为( )
A、y=6x+3 B、y=-6x-3 C、y=6x-3 D、y=-6x+3
7、某人沿着坡度为i=1∶![]() 的山坡前进了100米,那么这个人上升的高度为( )
的山坡前进了100米,那么这个人上升的高度为( )
A、100 m
B、50 m C、50![]() m D、以上答案都不对
m D、以上答案都不对
8、如果函数y=kx+b的图象经过第二、三、四象限则( )
A、k>0 b>0 B、k>0 b<0 C、k<0 b>0 D、k<0 b<0
9、函数y=ax+a的图是( )
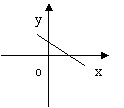 | 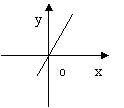 | 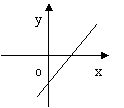 | 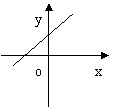 |
A B C D
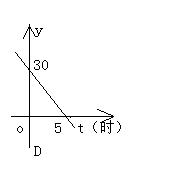
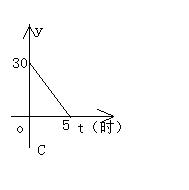
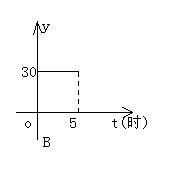
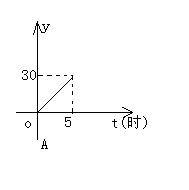 10、某水池蓄水30m3,打开阀门后每小时流出6m3,放水后池内剩下的水的立方数y(m3)与放水时间t(小时)之间的函数关系用图象表示为( )
10、某水池蓄水30m3,打开阀门后每小时流出6m3,放水后池内剩下的水的立方数y(m3)与放水时间t(小时)之间的函数关系用图象表示为( )
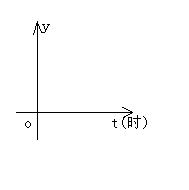 |
三、解答题:(5×6=30分)
1、![]() 2、解方程
2、解方程![]()
3、解方程![]() 4、解方程组
4、解方程组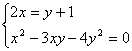
5、已知直线y=kx+b经过点(—2,—1),且点A(3,—3)也在此直线上,求(1)此函数的解析式;(2)求此函数图象与两坐标轴的交点坐标。
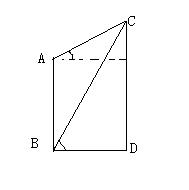 6、如图,河边有一高为20米的建筑物AB,它的正对岸有另一建筑物CD,从点A望点C,测得点C的仰角为30°,从点B望点C,测得点C的仰角为60°,求CD的高度和河面BD的宽度。
6、如图,河边有一高为20米的建筑物AB,它的正对岸有另一建筑物CD,从点A望点C,测得点C的仰角为30°,从点B望点C,测得点C的仰角为60°,求CD的高度和河面BD的宽度。
四、(6×4=24分)
1、 仓库存米1200吨,每天运出8吨。(1)列出仓库内剩下的米的吨数Q与运米的时间t之间的函数关系式;(2)求出函数自变量t的取值范围;(3)在直角坐标系内画出该函数的图象。
2、 某商店从厂家以每件21元的价格购进一批商品,该商店可以自行立价,若每件商品售价为a元,则可卖出(350—10a)件,但物价局限定每次商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品售价为多少元?
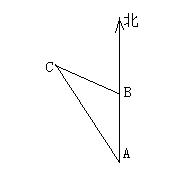 3、如图,某轮船沿正北方向航行,在A处测得灯塔C在北偏西30°,船以20海里/时的速度航行2小时后到达B处,测得灯塔在北偏西45°,又知在灯塔C 50海里内有暗礁,试问该船有无触礁危险?试计算说明。
3、如图,某轮船沿正北方向航行,在A处测得灯塔C在北偏西30°,船以20海里/时的速度航行2小时后到达B处,测得灯塔在北偏西45°,又知在灯塔C 50海里内有暗礁,试问该船有无触礁危险?试计算说明。
4、已知关于x的方程x2-2(k+1)x+k2+12=0的两个实数根的平方和是一个直角三角形的斜边的平方,这个直角三角形的两直角边的差是2,求k的值。