初三数学易错题
代数
第一章∶一元二次方程
1、解方程
的过程中若会产生增根，则m=＿＿＿＿
2.关于x的方程m2x2＋（2m＋1）x＋1=0有两个不相等的根，求m的取值范围＿＿
3，若关于x的方程ax2－2x＋1=0有实根，那a范围＿＿＿＿
4，已知方程3x2－4x－2=0,则x1－x2=＿＿＿,大根减小根为＿＿＿＿
5，以
和
的一元二次方程是＿＿＿＿
6,若关于x的方程（a+3）x2－（a2－a－6）x＋a=0的两根互为相反数，则a=＿＿＿
7，已知a,b为不相等的实数，且a2－3a＋1=0,b2-3b+1=0则
＋
=＿＿＿
8，方程ax2＋c=0（a≠0）a,c异号，则方程根为＿＿＿＿＿
9,若方程3x2＋1=mx的二次项为3x2,则一次项系数为＿＿＿＿＿
23,分解因式4x2＋8x＋1=＿＿＿＿＿
24,若方程2x2＋3x－5=0的两根为x1 ,x2 则x12＋x22=＿＿＿＿＿
25,方程组
有两组相同的实数解，则k=＿＿＿方程组的解为＿＿＿
43，若x是锐角，cosA是方程2x2－5x＋2=0的一个根，则∠A=＿＿＿
1、已知：Rt△ABC中,∠C=900,斜边c长为5 ,两条直角边a,b的长分别是 x2-(2m-1)x+4(m-1)=0的两根,则m的值等于 ( )
A. –1 B. 4 C.-4或1 D. –1或4.
2、已知关于x的方程
有两个不相等的实数根，则m的范围是：( ) A．m<3 B. 
C. 
D. 
3、已知方程①
，②
,③
,
④
，⑤
其中一定有实数解的方程有
A、1个 B、2个 C、3个 D、4个
5、已知 
那么代数式
的值是
( )
(A)2000 (B)-2000 (C)2001 (D)-2001
6,下面解答正确的是( )
A， 分式
的值是零，x=-2或x=1
B, 实数范围内分解因式2x2＋x－2=
C, x=-1是无理方程
的根
D, 代数式x2＋2x－1通过配方法知x=-1时，它有最小值是－2
7，关于x的方程x2－mx＋n=0有一正一负的两实根，且负根绝对值较大，则（ ）
A， n＞0, m＜0 B,n>0, m＞0, C, n<0 m>0 D,n＜0 m<0
8,若 
则有（ ）
A，ax2+bx+c=0 B,ax2+bx-c=0 C,ax2-bx+c=0 D, ax2-bx-c=0
9、在Rt△ABC中，∠C=900，a、b、c分别是∠A、∠B、∠C的对边，a、b是关于x的方程
的两根，那么AB边上的中线长是（ ）
（A） 
（B）
（C）
5 （D）2
20，已知关于x的方程x2＋px＋q=0的两根为x1=－3 x2=4,则二次三项式x2－px＋q=（ ）
A.（x＋3）（x－4） B, （x－3）（x＋4） C,（x＋3）（x＋4）D,（x－3）（x－4）
三, 解答题
1,甲乙二人合作一项工程，4天可完成，若先有甲单独做3天，剩下的由乙独做，则以所用的时间等于甲单独完成这项工程的时间，求甲乙二人单独完成此项工程各需几天？
2，解方程mnx2－（m2＋n2）x＋mn=0 （mn≠0）
3，在⊿ABC中，∠A ∠B ∠C 的对边分别为a,b,c且a,b是关于x的方程∶x2－（c＋4）x＋4c＋8=0的两根，若25asinA=9c,求⊿ABC的面积
第二章∶函数
第一节∶平面直角坐标系
22，平面直角坐标系中，点A（1－2a,a-2）位于第三象限且a为整数，则点A的坐标是＿＿＿＿＿
10、已知点
在第二象限，则a的取值范围是（ ）
（A）
（B）
（C）
（D）
14、若点M（x－1,1－y）在第一象限，则点N（1－x，y－1）关于x轴的对称点在（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
第二节∶函数
11、函数
中，自变量x的取值范围是＿＿＿＿
12、函数
的自变量的取值范围是＿＿＿＿＿
1，锐角三角形ABC内接于⊙O，∠B=2∠C，∠C所对圆弧的度数为n，则n的取值范围是 （ ）A, 0°＜n＜45° B, 0°＜n＜90° C, 30°＜n＜45° D,60°＜n＜90°
第三节∶一次函数
15，当＿＿＿时，函数y=（m＋3）x2m＋3＋4x－5（x≠0）是一个一次函数。
16，若直线y=kx+b经过第一，三，四象限，则直线y=bx+k过＿＿＿＿象限
17.已知函数y=3x+1,当自变量x增加h时，函数值增加＿＿＿＿
19,下列图形中，表示一次函数y=mx+n与正比例函数y=mnx.(m,n是常数且mn≠0)图像的是（ ）
18，已知直线l与直线y=2x+1的交点的横坐标是2,与直线y=-x+2的交点的纵坐标为1，求直线l解析式为＿＿＿＿
19.已知y与x成正比例，若y随x增大而减小，且其图像过（3，－a）和（a,-1）两点则此解析式为＿＿＿＿＿
20，直线y=ax-3与y=bx+4交于x轴上同一点，则a∶b=＿＿＿＿
21,若一次函数y1=（m2－4）x＋1－m与一次函数y2=（m2－2）x＋m2－3的图像与y轴交点的纵坐标互为相反数，则m=＿＿＿＿
11．不论m何实数，直线
与
的交点不可能在（ ）
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
17，对于不同的k值，函数y=kx+4(k≠0）时不同直线，则这些直线一定（ ）
A, 互相平行 B, 相交于一点 C, 有无数个交点 D, k＞0交于一点，k<0交于另一点
11，一次函数y=kx+b的图像经过点（m,-1）（1,m）,其中m＜－1，则k,b满足的条件（ ）
A,k＜0,b＜0 B,k＞0,b＞0 C,k＜0,b＞0 D,k＞0,b＜0
第四节∶二次函数
1,二次函数的一般形式是＿＿＿＿＿，它的解为＿＿＿＿＿
13、抛物线
与y轴交于点A，与x轴的正半轴交于B、C点，且BC=2，
，则b=＿＿＿＿＿
14、若抛物线
与x轴有交点，则k的取值范围是＿＿＿。
16，已知等腰三角形ABC周长为20，则底边y与腰长x的函数关系式是＿＿＿＿＿＿
自变量的取值范围是＿＿＿＿＿
11,抛物线y=x2+（m-4）x－4m，若顶点在y轴上，则m=＿＿＿若顶点在x轴上，则m=＿＿＿
11,若二次函数y=mx2－（m－2）x－1的图像与x轴交于点A（a,0）B（b,0）且a+b=ab则m =＿＿＿＿
12,用30厘米的铁丝围成的矩形最大面积可以达到＿＿＿＿厘米
12，如图，用12米长的木方，作一个有一条横档的矩形窗子，为使透
进的光线最多，应选窗子的长宽各为＿＿＿米
11，抛物线y=x2+11x－2m于x轴交于（x1,0）（x2,0），已知x1x2=x1＋x2－15,要是次抛物线经过原点，应将它向＿＿平移＿＿＿个单位。
12，函数y=-2（x＋3）2＋2的对称轴是＿＿＿，于x轴的交点为＿＿＿，于y轴的交点为＿＿＿
11，已知函数y=-
x＋2,当－1＜x≤1时，y的取值范围（
）
13，已知抛物线y=ax2＋bx,当a＞0,b＜0时，它的图像过（ ）
A,一，二，三，象限 B,一，二，四象限 C,一，三，四象限
D，一，二，三，四象限
13，不论x为何值，函数y=ax2＋bx＋c（a≠0）的值小于0的条件是
（ ）A,a＜0 ⊿＜0 B,a＞0 ⊿＜0 C,a＜0 ⊿＞0 D,a＞0 ⊿＜0
16、下列四个函数：①
；②
；③
；④
；⑤
；⑥
。其中，在自变量的允许值范围内，y随x的减小而减小的函数个数为（ ）
A、1 B、2 C、3 D、4
18、下列四个函数中，y的值随着x值的增大而减小的是（ ）
（A）
（B）
（C）
（D）
第五节∶反比例函数
1，已知反比例函数的图像经过点（a,b）,则它的图像一定经过（ ）
A,（－a,b） B,(a,-b) C,(-a,b) D,(0,0)
2,下列函数中，反比例函数是（ ）
A,x(y-1)=1 B,
C,y=1/x2 D,y=1/3x
3，若y与－3x成反比例，x与
成正比例，则y是z的（ ）
A,正比例函数 B,反比例函数 C,一次函数 D,不确定
第三章∶统计初步
2，已知一组数据x1,x2,x3,x4的平均数是2，方差是1，则另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数和方差分别是＿＿＿＿
2，对60名学生的测量身高，落在167.5～170.5cm之间的频率是0.3，未落在这个区间的学生人数是＿＿＿＿人。
21,下列语句正确的是( )
A,四个班的平均成绩分别是a,b,c,d,则这四个班的总体评剧成绩为
B, 方差都为正数 C,标准差都为正数 D,众数，中位数，平均数有可能一样
几何
第一章∶三角函数
1、在Rt△ABC中，∠C=90°，tanA+2cotA=
，AC=2，则AB=＿＿＿＿
2，sinA=
,求cos
=＿＿＿
6,sin221°39′＋sin2α=1，α=＿＿＿
7，（1＋sin45°－cos30°）（1－sin45°－cos30°）=＿＿＿
29, 
30，若A是锐角，且sinA=
则tanA=＿＿＿＿＿
31,比较大小∶ sinα＿＿＿＿tanα （α为锐角）
32,在⊿ABC中，a=2b=
c,则tanC=＿＿＿＿
33,利用正切和余切的倒数关系消去公式1／cot38°21′中的分母为＿＿＿
36，计算 cos21°＋cos22°＋cos23°＋- - -＋cos288°＋cos289°=＿＿＿＿
37，在等腰Rt⊿ABC中，∠C=90°，AD是中线，则∠DAC的余弦值是＿＿＿＿
38，tan230°＋2sin60°＋tan45°×sin90°－tan60°＋cos230°=＿＿＿＿
39，等腰⊿ABC的腰长为2cm,面积为1cm2,其顶角度数为＿＿＿＿＿
41，tanA=2,
=＿＿＿＿＿＿
42，已知sinα＋cosα=3／2,则sinα×cosα=＿＿＿＿
1，一直角三角形的两边长为3，4，则较小角的正切值时（ ）
A，3／4 B,4／3 C,3／4 或 
D，以上答案都不对
2、在△ABC中，∠C＝90°，△ABC面积为5cm2 ,斜边长为4cm,则tanA+cotB的值为( )
(A) 
(B)
(C)
(D)
3，若α为锐角，sinα＞cos30°，则α的取值范围（ ）
A,0＜α＜30° B,30°＜α＜60° C,α＞60° D,60°＜α＜90°
第二章∶解直角三角形
3.在高2m，坡角为30°的楼梯表面铺地毯，地毯长度至少需＿＿＿m
4.在Rt⊿ABC中，∠ACB=90°，CD为斜边上的高，BD＝3，AD＝16／3则sinA＝＿
5.以坡面长为4
米，水平宽为2
米，则这个坡面的坡角为＿＿＿
第三章∶圆
第一节∶圆的有关性质
8、如图，锐角△ABC中，以BC为直径的半圆O分别交AB，AC于D、E两点，且
,则cosA=＿＿＿＿＿
11,一弦分圆周为5∶7，此弦所对的圆周角为＿＿＿＿
12，在半径为5cm的圆内有长为5
cm的弦，则此弦所对的圆周角为＿＿＿＿＿
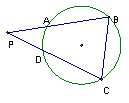15，⊙O的半径为5cm弦AB∥CD，AB=6cm,CD=8cm，则两弦之间的距离为＿＿＿＿
16，已知，如图，∠P=40°, 
则∠ACD=＿＿＿＿
27，已知A,B,C三点在⊙0上，且∠A0B=1000，则∠C=＿＿＿＿
28，已知⊙0的半径为5cm,A为线段OP中点，当OP=6cm 时，点A与⊙0的位置关系是＿＿＿＿＿＿＿＿
40，一直顶角A＝50°的等腰⊿ABC内接⊙0，D为圆周上一点，则∠ADB度数为＿＿＿
18，在⊿ABC中，AB=AC=13cm，BC=10cm,求⊿ABC的外接圆半径R=＿＿＿＿
第二节∶直线与圆
13，正⊿ABC的边长为a,则它的高为＿＿＿内切圆半径为＿＿＿外接圆直径为＿＿＿
14,已知⊿ABC中，∠C＝90°，AC＝9cm,BC＝12cm，以C为圆心，AC为半径作圆交BA于D，则AD长为＿＿＿＿
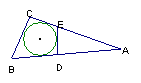17，圆中最大弦长为12，若直线与圆相交，设直线与圆心的距离为d，则d的取值范围＿＿＿＿
18，如图⊙O是⊿ABC的内切圆⊙0的切线DE交AB于D，交AC于E ①若DE=6，BC=8，则四边形DBCE的周长为＿＿＿＿②若⊙O的半径为6，OA=10，则⊿ADE的周长为＿＿＿＿
19、已知P是△ABC的内心，O是△ABC的外心，若∠BPC=125°则∠BOC＿＿
20、如图，点P是半径为5的⊙O内一点，且OP=3，在过点P的所有⊙O的弦中，弦长为整数的弦的条数为＿＿＿＿＿
21，AB是⊙O的弦，P是AB上的一点，AB=10cm，PA=4cm，OP=5cm
则⊙O的半径为＿＿＿＿＿＿＿
22，已知顶角A等于50°的等腰三角形ABC内接⊙O,D为圆周上一点,则∠ADB的度数为＿＿＿＿＿
23，已知⊙0直径AB＝2cm,AD=cm,那麽弧CD的度数为＿＿＿
24，已知⊙O的半径为2cm，弦AB的长为2cm，求这弦中点到这条弦所对的弧中点的距离为＿＿＿＿
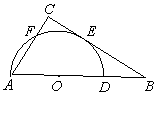25，圆的弦长等于它的半径，这条弦所对的圆周角的度数为＿＿＿＿
13．如图：△ABC中∠C=90°，AC=3，BC=4，
D在边AB上，以AD为直径的半圆切BC于E，
交AC于F，则BD = ______________.
26，⊙O中弦AB,CD互相垂直，垂足为E，AE=2,EB=6,ED=3,则⊙0半径为＿＿＿
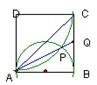34，PAB为⊙O的割线，PO交⊙O于C，若⊙O的半径为R，PO=d，则PA×PB=( )A,2R－2d B,2R+2d C, d2—R2 D, R2－d2
35，如图，已知正方形ABCD，以D为圆心，以DA为半径的圆与以AB为直径的圆交于P,AP的延长线交BC于Q，则CQ与QB的关系是（ ）
A, CQ=QB B, CQ＞QB C, CQ＜QB D, 无法确定
4、如图，圆外切等腰梯形ABCD的中位线EF= 15 cm，那么等腰梯形ABCD的周长等于 （ ）（A）15 cm（B）20 cm （C）30 cm（D）60 cm
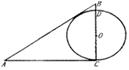5.如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，以BC上一点O为圆心作⊙O与AC、AB都相切，又⊙O与BC的另一个交点为D，则线段BD的长为（ ）
（A）1 （B）
（C）
（D）
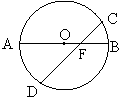6、如图，已知⊙O的直径AB与弦CD交于点F，∠AFD＝450，AB＝
，则FC2＋FD2＝_______.
A． 2
B. 
C.
1 D.不确定
7.⊙O的直径AB＝5，弦BC＝4，∠ABC的平分线交半圆于点D，延长AD、BC交于E，则
的值为（ ）A、9 B、8 C、7 D、6
8、相交两圆的公共弦长为24cm,两圆的半径长分别为15cm和20cm,则这两个圆的圆心距等于 （ ）A．16cm B. 9cm或16cm C. 25cm D.7cm和25cm
9.如果两圆心都在X轴上,⊙O1的圆心坐标为(7,0),半径为1;⊙O2的圆心坐标为(X,0),半径为2,当2<X<4时,两圆的位置关系是( ) A.相交 B.相切 C.外离 D.内含
10.在直角三角型ABC中，∠C=60°，以AB为直径的半圆交斜边BC于D，则△ACD与△ABD的面积之比为 ( ) A.1:2 B.1:3 C.2:3 D.3:4
11、使用直角钢尺检查某一工件是否恰好是半圆形的凹面，成半圆形的为合格，如图所示的四种情况中合格的是 （ ）
15.在⊙O中，弦AB=2CD，则（ ）
A，
B, 
C, 
D,不能确定
16、四边形ABCD内接于圆，∠A、∠B、∠C、∠D的度数比依次可以是（ ）
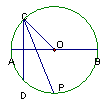（A）1：2：3：4 （B）6：7：8：9 （C）4：1：3：2 （D）4 ：3：1：2
19，已知点P到⊙0最大距离为a,最小距离为b(a>b)则此圆的半径为（ ）
21,如图，AB为⊙0的一直径，它把⊙0分成上下两个半圆，自上半圆上一点C作弦CD⊥AB，∠OCP的平分线交⊙0于点P，当C在上半圆（不包括A,B两点）上移动时，则点P（ ）A, 到CD的距离保持不变 B,位置不变 C，等分弧DB D,随C移动而移动
1.已知，如图直径AB⊥CD，弦AE，CD延长线交于F，求证：AC×EF=CE×DF
1,如图，BC为直径，G为半圆上任意点，A为弧BG中点，AP⊥BC于P，求证AE=BE=EF
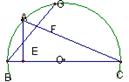
2，如图，⊿ABC中，AB=AC,BD平分∠B交AC于D，⊿ABD的外接圆交AC于E，求证AD＝EC
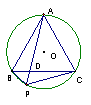
4，如图等边三角形ABC内接于圆，P为BC上任一点，AP交BC于D,求证∶PB和PC是方程x2－PA×x＋PA×PD=0的两根
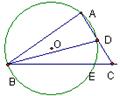
5，如图，从圆外一点P作圆的一条切线PA，A为切点，过点P作一直线与圆交于B，C两点，弦CD∥AP，PD与圆交于E，连结EB并延长交AP于M，求证：AM=PM
6，已知PBD是⊙0的割线，PA，PC是⊙0的切线，求证：①PA×PB＝PB×AD ②AD2／AB2 =PD／PB
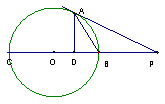7，P是⊙0直径CB延长线上一点，PA切⊙0于A，AD⊥BC于D，若PA=10，PB=5，求sin∠BAP的值
8，如图，BC为⊙O的直径，PA切⊙0与A，AB＝15，∠P的正弦值为3／5，求PC的长
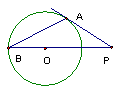
9，已知，如图，⊿ABC内接于⊙0，∠BAC的平分线交BC于D，交⊙0于E，⊙0的切线BF交AE延长线于F，过E作EH⊥BF，垂足为H，求证：①BE平分∠CBF ②BC＝2BH；③AD×EF=CD×BF
10,已知，如图PA,PB切⊙0于A,B求证 ∠OPC=∠OCM
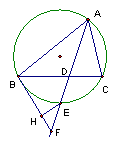
11，已知Rt⊿ABC，以o为圆心，OB为半径的圆交AB于E，且AC于D，延长ED，BC交于F，求证：BC=CF
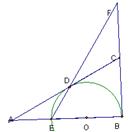
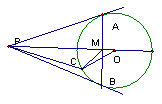
第三节∶圆与圆
9、直径分别为12和4的两个圆的圆心距是8，则这两个圆共有＿＿条公切线。
10，⊙01与⊙02相交于AB，它们的半径分别为 r1=3 r2=5,AB=4,则o1o2=＿＿＿＿
11，若两圆半径分别为9cm和4cm,圆心距为10cm，则这两圆的外公切线长为＿＿＿＿
它们的夹角为＿＿＿＿
12，⊙o1和⊙O2相交于A,B两点，⊙O1和⊙O2的半径分别为2和
，公共弦长为2，
∠O1AO2的度数为＿＿＿＿，圆心距为＿＿＿＿
11,在下列四个命题中，正确的是（ ）
A，两圆的外公切线的条数不小于它们的内公切线的条数
B,相切两圆共有三条公切线 C,无公共点的两圆必外离
D,两圆外公切线的长等于圆心距
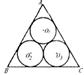12.如图，三个半径为r的等圆两两外切，且与△ABC的三边分别相切，则△ABC的边长为（ ）
（A）2r (B)
(C)3r (D)
12，命题：（1）两圆相切，连心线段过切点 （2）两圆相交公共弦一定不平分连接两圆心的线段（3）两圆内切，过切点有一条内公切线，其中正确的个数是（ ）
A,1 B,2 C,3 D,4
13、已知两圆半径之比R：r=7：3，两圆内切时的圆心距d=6， 若两圆相交，则d为( )
(A)5 (B)12 (C)15 (D)18
14、现有半径为R的两圆外切，能与这两圆都相切且半径为2R的圆共有( )
(A)5个 (B)4个 (C)3个 (D)2个
3，如图，⊙0与⊙A相交于C,D，A在⊙0上，过A的直线交⊙A于E，B求证 AE2＝AF×AB
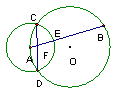
6，如图⊙O1 ⊙O2外切于点A，BC为⊙O1
⊙O2的外公切线，B,C为切点，连心线O1O2交BC于P，求证∶（1）AB⊥AC（2）PA2=PB×PC
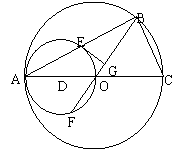
10.已知：如图，ΔABC内接于⊙O，AC是⊙O的直径，以AO为直径的⊙D交AB于E，交BO的延长线于F，EG切⊙D于E，交OB于G，求证：（1）AE＝BE，（2）EG⊥OB，（3）2AE2=GF•AC
第四节∶正多边形与圆