2005年安徽省初中升学统一数学试题
一、选择题(本题共10小题,每小题4分,共40分).
1.计算2-(-1)2等于( )
A.1 B.0 3.-1 D.3
2.化简x-y-(x+y)的最后结果是( )
A.0 B.2x C.-2y D.2x-2y
3.用两个完全相同的直角三角板,不能拼成下列图形的是( )
A.平行四边形 B.矩形 C.等腰三角形 D.梯形
4.我国“杂交水稻之父”袁隆平主持研究的某种超级杂交水稻平均亩产820千克.某地今年计划载插这种超级杂交水稻3000亩,预计该地今年收获这种超级杂交水稻的总产量(用科学记数法表示)是( )
A.![]() 千克
B.
千克
B.![]() 千克 C.
千克 C.![]() 千克 D.
千克 D.![]() 千克
千克
5.分解因式a-ab2的结果是( )
A.a(1+b)(1-b) B.a(1+b)2 C.a(1-b)2 D.(1-b)(1+b)
6.函数![]() 自变量x的取值范围是( )
自变量x的取值范围是( )
A.x≤![]() B.x≥
B.x≥![]() C.x≥
C.x≥![]() D.x≤
D.x≤![]()
7.某市社会调查队对城区内一个社区居民的家庭经济状况进行了调查,结果是:该社区共有500户,高收入、中等收入和低收入家庭分别有125户、280户和95户.已知该市有100万户家庭,下列表述正确的是( )
A.该市高收入家庭约25万户 B.该市中等收入家庭约56万户
 C.该市低收入家庭约19万户
C.该市低收入家庭约19万户
D.因为城市社区家庭经济状况良好,所以不能据此估计全市所有家庭经济状况
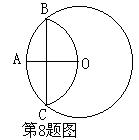
8.如图,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
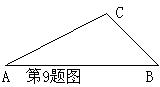 9.如图,在△ABC中,∠A=30°,tanB=
9.如图,在△ABC中,∠A=30°,tanB=![]() ,AC=
,AC=![]() ,则AB=( )
,则AB=( )
A.4 B.5 C.6 D.7
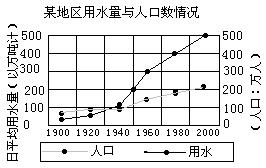
10.下图是某地区用水量与人口数情况统计图.日平均用水量为400万吨的那一年,人口数大约是( )
A.180万 B.200万 C.300万 D.400万
二、填空题(本题共5小题,每小题4分,共20分)
 11.冬季的某日,上海最低气温是3℃,北京最低气温是-5℃,这一天上海的最低气温比北京的最低气温高______℃.
11.冬季的某日,上海最低气温是3℃,北京最低气温是-5℃,这一天上海的最低气温比北京的最低气温高______℃.
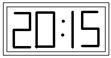
 12.在平面镜里看到背后墙上,电子钟示数如图所示,这时的实际时间应该是______.
12.在平面镜里看到背后墙上,电子钟示数如图所示,这时的实际时间应该是______.
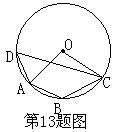
13.如图,ABCD是⊙O的内接四边形,∠B=130°,则∠AOC的度数是______.
14.某射击运动爱好者在一次比赛中共射击10次,前6次射击共中53环(环数均是整数),如果他想取得不低于89环的成绩,第7次射击不能少于_____环.
15.写出一个图象经过点(-1,-1),且不经过第一象限的函数表达式______.
三、(本题共2小题,每小题8分,共26分)
16.当a=![]() 时,求
时,求![]() 的值.
的值.
17.小明的爷爷退休生活可丰富了!下表是他某日的活动安排.和平广场位于爷爷家东400米,老年大学位于爷爷家西600米.从爷爷家到和平路小学需先向南走300米,再向西走400米.
(1)请依据图示中给定的单位长度,在图中标出和平广场A、老年大学B与和平路小学的位置.
(2)求爷爷家到和平路小学的直线距离.
| 早晨6:00—7:00 与奶奶一起到和平广场锻炼 |
| 上午9:00—11:00 与奶奶一起上老年大学 |
| 下午4:30—5:30 到和平路小学讲校史 |

四、(本题共2小题,第18题6分,第19题10分,共16分)
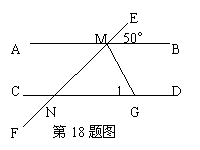 18.如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G.求∠1的度数.
18.如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G.求∠1的度数.
19.右图的花环状图案中,ABCDEF和A1B1C1D1E1F1都是正六边形.
(1)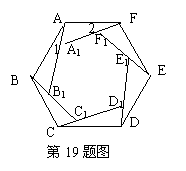 求证:∠1=∠2;
求证:∠1=∠2;
(2)![]() 找出一对全等的三角形并给予证明.
找出一对全等的三角形并给予证明.
五、(本题共2小题,每小题10分,共20分)
20.张新和李明相约到图书城去买书,请你根据他们的对话内容(如图),求出李明上次所买书籍的原价.

 21.已知函数y1=x-1和y2=
21.已知函数y1=x-1和y2=![]() .
.
(1)在所给的坐标系中画出这两个函数的图象;
(2)求这两个函数图象的交点坐标;
(3)观察图象,当x在什么范围内时, y1>y2?
六、(本题满分12分)
22.某校为了了解全校400名学生参加课外锻炼的情况,随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查,结果如下:(单位:分)
40 21 35 24 40 38 23 52 35 62
36 15 51 45 40 42 40 32 43 36
34 53 38 40 39 32 45 40 50 45
40 40 26 45 40 45 35 40 42 45
(1)补全频率分布表和频率分布直方图.
| 分组 | 频数 | 频率 |
| 14.5-22.5 | 2 |
|
| 22.5-30.5 | 3 | |
| 30.5-38.5 | 10 | 0.250 |
| 38.5-46.5 | 19 | |
| 46.5-54.5 | 5 | 0.125 |
| 54.5-62.5 | 1 | 0.025 |
| 合计 | 40 | 1.00 |
(2)填空:在这个问题中,总体是_____,样本是_____.
由统计结果分析的,这组数据的平均数是38.35(分),众数是_____,中位数是______.
(3)如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?
(4)估计这所学校有多少名学生,平均每天参加课外锻炼的时间多于30分?
七、(本题满分12分)
23.一列火车自A城驶往B城,沿途有n 个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,运行时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发往下面行程中每个车站的邮包一个.
例如,当列车停靠在第x 个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包共(x-1)个,还要装上下面行程中要停靠的(n-x)个车站的邮包共(n-x)个.
(1)根据题意,完成下表:
| 车站序号 | 在第x车站启程时邮政车厢邮包总数 |
| 1 | n-1 |
| 2 | (n-1)-1+(n-2)=2(n-2) |
| 3 | 2(n-2)-2+(n-3)=3(n-3) |
| 4 | |
| 5 | |
| … | …… |
| n |
(2)根据上表,写出列车在第x车站启程时,邮政车厢上共有邮包的个数y(用x、n表示).
(3)当n=18时,列车在第几个车站启程时邮政车厢上邮包的个数最多?
八、本题满分14分)
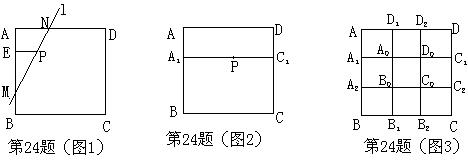
24.在一次课题学习中活动中,老师提出了如下一个问题:
点P是正方形ABCD内的一点,过点P画直线l分别交正方形的两边于点M、N,使点P是线段MN的三等分点,这样的直线能够画几条?
经过思考,甲同学给出如下画法:
如图1,过点P画PE⊥AB于E,在EB上取点M,使EM=2EA,画直线MP交AD于N,则直线MN就是符合条件的直线l.
根据以上信息,解决下列问题:
(1)甲同学的画法是否正确?请说明理由.
(2)在图1中,能否画出符合题目条件的直线?如果能,请直接在图1中画出.
(3)如图2,A1、C1分别是正方形ABCD的边AB、CD上的三等分点,且A1C1∥AD.当点P在线段A1C1上时,能否画出符合题目条件的直线?如果能,可以画出几条?
(4)如图3,正方形ABCD边界上的A1、A2、B1、B2、C1、C2、D1、D2都是所在边的三等分点.当点P在正方形ABCD内的不同位置时,试讨论,符合题目条件的直线l的条数的情况.
参考答案
一.选择题
1.A;2.C;3.D;4.C;5.A;6.D;7.D;8.B;9.B;10.A.
二.填空题
11.8; 12.21:05; 13.100; 14.6; 15.答案不唯一,如y=-x-2,或y=-x2等;
三.16.原式=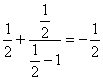 ;
;
17.(1)图略;(2)![]() (m).
(m).
四.18.由∠EMB=50°,所以∠BMF=130°,又MG平分∠BMF,所以∠BMG=![]() ∠BMF=65°,而AB∥CD,所以∠1=∠BMG=65°.
∠BMF=65°,而AB∥CD,所以∠1=∠BMG=65°.
19.(1)多边形ABCDEF与A1B1C1D1E1F1都是正六边形,所以∠1+∠A1AF=120°,∠2+A1AF=∠B1A1F1=120°,所以∠1+A1AF=∠2+∠A1AF,即∠1=∠2;(2)△ABB1≌△FAA1.因为∠F1A1B1=∠A1B1C1=120°,所以∠AB1B=∠FA1A=60°,又AB=FA,∠1=∠2,所以△ABB1≌△FAA1.
五.20.设李明上次购买书籍的原价是x元,由题意有0.8x+20=x-12,解得x=160.
21.(1)略;(2)解x-1=![]() ,得
,得![]() ,即y1=x-1和y2=
,即y1=x-1和y2=![]() 的两个交点坐标分别为A(-2,-3),B(3,2);(3)观察图象可知,当-2<x<0或x>3时, y1>y2.
的两个交点坐标分别为A(-2,-3),B(3,2);(3)观察图象可知,当-2<x<0或x>3时, y1>y2.
六.22.(1)自上而下依次是0.075和0.475,图略;(2)全校400名学生平均每天参加课外锻炼的时间,40名学生平均每天参加课外锻炼的时间,40,40;(3)用平均数、众数和中位数描述该校400名学生平均每天参加课外锻炼时间的总体情况都比较合适.因为在这一问题中,这三个量非常接近;(4)因为随机调查的40名学生平均每天参加课外锻炼的时间多于30分的有35人,所以可以估计这所学校平均每天参加课外锻炼的时间多于30分的学生有35÷40×400=350人.
七.23.(1)
| 车站序号 | 在第x车站启程时邮政车厢邮包总数 |
| 1 | n-1 |
| 2 | (n-1)-1+(n-2)=2(n-2) |
| 3 | 2(n-2)-2+(n-3)=3(n-3) |
| 4 | 3(n-3)-3+(n-4)=4(n-4) |
| 5 | 4(n-4)-4+(n-5)=5(n-5) |
| … | …… |
| n | 0 |
(2)y=x(n-x);(3)当n=18时,y=x(18-x)=-x2+18x=-(x-9)2+81,当x=9时,y 取得最大值.所以列车在第9个车站启程时,邮政车厢上邮包的个数最多.
八.24.(1)的画法正确.因为PE∥AD,所以△MPE~△MNA,所以![]() ,而EM=2EA,所以MP:MN=2:3,因此点P是线段MN的一个三等分点.(2)能画出一个符合题目条件的直线,在EB上取M1,使EM1=
,而EM=2EA,所以MP:MN=2:3,因此点P是线段MN的一个三等分点.(2)能画出一个符合题目条件的直线,在EB上取M1,使EM1=![]() AE,直线M1P就是满足条件的直线,图略;(3)若点P在线段A1C1上,能够画出符合题目条件的直线无数条,图略;(4)若点P在A1C1,A2C2,B1D1,B2D2上时,可以画出无数条符合条件的直线l;当点P在正方形A0B0C0D0内部时,不存在这样的直线l,使得点P是线段MN的三等分点;当点P在矩形ABB1D1,CDD2B2,A0D0D2D1,B0B1B2C0内部时,过点P可画出两条符合条件的直线l,使得点P是线段MN的三等分点.
AE,直线M1P就是满足条件的直线,图略;(3)若点P在线段A1C1上,能够画出符合题目条件的直线无数条,图略;(4)若点P在A1C1,A2C2,B1D1,B2D2上时,可以画出无数条符合条件的直线l;当点P在正方形A0B0C0D0内部时,不存在这样的直线l,使得点P是线段MN的三等分点;当点P在矩形ABB1D1,CDD2B2,A0D0D2D1,B0B1B2C0内部时,过点P可画出两条符合条件的直线l,使得点P是线段MN的三等分点.
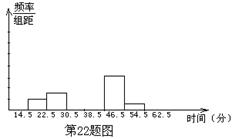 0.050
0.050