2006年崇明县初三数学质量测试试卷 2006.4.27
（满分150分，考试时间100分钟）
一、填空题：（本大题共12题，满分36分）
【只要求直接填写结果，每个空格填对得3分，否则得0分】
1．
的相反数是____________________.
2．因式分解：
3．不等式组
解集是_____________________.
4．方程
的解是___________________.
5．据测算，我国每天因土地沙漠化造成的经济损失平均为元，这个数用科学记数法表示为________________________.
6. 函数
的定义域为________________________.
7. 如果方程
的两个实数根分别是
,
那么
8．如果一元二次方程
有两个不相等的实数根,
那么实数
的取值范围是________________________.
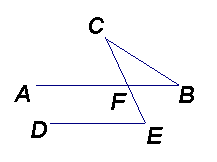
9．如图, 已知AB//DE, 
,
那么
的度数是__________________.
10．已知两个相似三角形对应高的比是1:2 ,那么它们的面积比是_________________.
11．两圆内切,其中一圆的半径是5, 两圆的圆心距为2,
那么另一圆的半径为______________________.
12．如图, DE是
的中位线,M是DE的中点,
CM的延长线交AB于N,
那么
=_________________.
二、选择题：（本大题共4题，满分16分）
【下列各题的四个结论中，有且只有一个结论是正确的，把正确结论的代号写在题后的圆括号内，选对得4分；不选、错选或者多选得0分】
13．下列运算中, 正确的是……………………………………………………………( )
(A) 
(B)
(C) 
(D)
14．已知直线
, 当
时, 直线不经过…………………………………( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
15．下列图形中, 既是中心对称图形, 又是轴对称图形的是…………………………( )
(A) 等边三角形 (B) 等腰梯形 (C) 圆 (D) 平行四边形
16．下列命题中, 真命题是……………………………………………………………( )
(A) 对角线相等的四边形是矩形
(B) 对角线互相垂直且相等的四边形是正方形
(C) 对角线互相垂直的四边形是菱形
(D) 对角线互相平分的四边形是平行四边形
三、（本大题共5题，满分48分）
17．（本题满分9分）
计算：．
+
解：
18．（本题满分9分）
解方程组: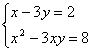 
解：
19．（本题满分10分）
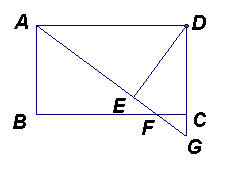如图, 在矩形ABCD中，F是BC边上的一点, AF的延长线交DC的延长线于G,
DE
AG于E, 且DE=DC.
求证: 
≌
证明：
20．（本题满分10分）
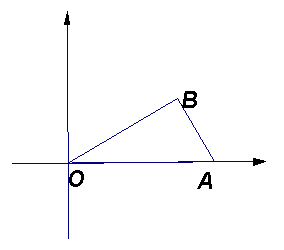
如图, 已知O为坐标原点，
,
,且点A的坐标为(2, 0).求:
(1) 点B的坐标;
(2)
若二次函数
的图象过
A、B、O三点，求此二次函数的解析式,
并用配方法求出其顶点坐标.
解：
21．（本题满分10分）
某研究性学习小组，为了了解本校初一学生一天中做家庭作业所用的大致时间(时间以整数记，单位：分钟)，对本校的初一学生做了抽样调查，并把调查得到的所有数据(时间)进行整理，分成五个时间段，绘制成统计图(如图所示)，请结合统计图中提供的信息，回答下列问题：
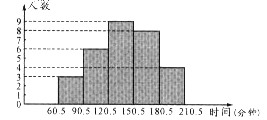
(1)这个研究性学习小组所抽取样本的容量是多少?
(2)在被调查的学生中，一天做家庭作业所用的大致时间超过120分钟(不包括120分钟)的人数占被调查学生总数的百分之几?
(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内?
解：
四、（本大题共4题，满分50分）
22．（本题满分12分）
如图,已知BF、BE分别是△ABC中∠B及它的外角的平分线，AE⊥BE，E为垂足，
AF⊥BF，F为垂足，EF分别交AB、AC于M、N两点.
求证：(1) 四边形AEBF是矩形；
(2) 
.
证明：
23．（本题满分12分）
某商店以2400元购进某种盒装茶叶，第一个月每盒按进价增加20％作为售价,售出50盒,第二个月每盒以低于进价5元作为售价，售完余下的茶叶，在整个买卖过程中盈利350元,求每盒茶叶的进价．
解：
24．（本题满分12分）
如图，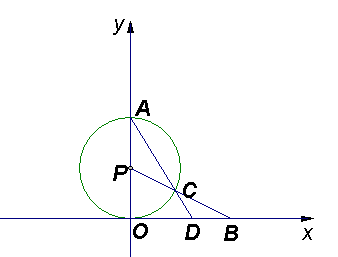
已知⊙P与
轴相切于坐标原点O，点A(0
,2)是⊙P 与
轴的交点，
点B
,连结BP交⊙P 于点C,连结AC并延长交轴于点D．
(1) 求线段BC的长；
(2) 求直线AC的函数解析式；
(3) 当点B在轴上移动时，是否存在点B，
使△BOP相似于△AOD? 若存在，
求出符合条件点的坐标;若不存在，请说明理由．
解：
25．（本题满分14分）
如图1,在四边形ABCD中，
，BC∥AD，BC=20，DC=16，AD=30，动点P从点D出发，沿射线DA的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P、Q分别从点D、C同时出发，当点Q运动到点B时，点P随之停止运动，设运动时间为t（秒）
(1)设△BPQ的面积为S，求S与t之间的函数关系式;
(2)当t为何值时，以B、P、Q三点为顶点的三角形是等腰三角形;
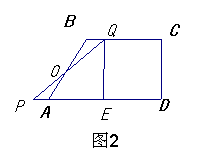
(3)当线段PQ与线段AB相交于点0，且2AO=OB时，求∠BQP的正切值;
(4)是否存在时刻t，使得PQ⊥BD?若存在，求出t的值;若不存在，请说明理由.
解：
2006年崇明县初三数学质量测试卷参考答案 2006.4
一、填空题（本题共12小题,每小题3分,满分36分）
1．3 2. 
3. 
4. =2 5. 
6. 
7. 
8. 
9. 
10. 1 :
4 11. 3或 7 12. 1 : 5
二、选择题（本题共4小题, 每小题4分, 满分16分）
13. B 14. B. 15. C. 16. D
三、（本大题共5题，第17、18题每题9分，第19~21题每题10分，满分48分）
17. 解：原式=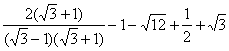 
……5分（每项各1分）
= 
……………2分(笫一、三项各1分)
= 
………………………………………………2分
18.解：
由（2）得
----（3）…………………………………2分
把（1）代入（3）得2=8…………………………………………1分
=4………………………………………………2分
把 =4代入（1）得 4-3
…………………………………1分
…………………………………………2分
原方程组的解为
…………………………………………1分
19．证明：
四边形ABCD为矩形
………………………………………………………2分
AB=DC…………………………………………………………2分
AD//BC…………………………………………………………2分
………………………………………………1分
…………………………1分
……………………1分
………………………………………………1分
20．解：（1）点A的坐标为（2，0） OA=2
在Rt△ABO中，
……1分 OB=OA
………1分
过B作BE
轴于E，在
中，
∵ BE=
……………1分 OE=
………1分
点B（
）……1分
（2）按题意可知
………………1分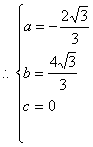 
……………………1分
所求二次函数的解析式为
……………………………1分
………1分 顶点坐标为（1，
）……1分
21、解：（1）样本的容量为3+4+6+8+9=30（人）………………………………3分
（2） 一天做家庭作业时间超过120分钟的人数为9+8+4=21………1分
占被调查人数的百分比为
……………………3分
（3）中位数落在120.5~150.5 这一时间段中……………………………3分
四、（本大题共4题，第22、23、24题每题12分，第25题14分，满分50分）
22.证明：
（1）BF、BE分别是中
及它的外角的平分线
……………………1分
……1分
…1分
四边形AEBF为矩形……………………………1分
（2）四边形AEBF为矩形 BM=MA=MF…………2分
……………………………1分
……………………………1分
MF//BC……………………………1分
M是AB的中点 N为AC的中点……………………………1分
MN为
ABC的中位线………………1分 
………1分
23．解：设每盒茶叶的进价为元. …………………1分
…………………5分
化简得：
…………2分 解之得：
…………2分
经检验，是方程的解，但
不符合题意，故舍去. ………1分
答：每盒茶叶的进价为40元. …………………1分
24.解：（1）由题意得：OP=1，OB=
，CP=1，在
中，
………………1分 BC=2 …………………1分
（2）过点C作
轴于E，则CE//AO
……………………………1分
…………………1分
……………………………………………1分
设直线AC的函数解析式为
…………………1分
∵
即直线AC的函数解析式为
………1分
3．在轴上存在点B，使
相似。
相似，则
……………………………1分
……………………………1分
……………1分
点坐标为（
………………………1分
根据对称性得
…………………………………………………1分
符合条件的B点坐标为
25．解：（1）过点P作
，垂足为M，则四边形MPDC为矩形.
∵QC=t ∴
……………1分
………………………1分
（2）由图1可知
i) 若PQ=BQ
在
由
得
…………1分 解得：
…………1分
ii) 若PB=BQ
在
中，
由
，得
…………………1分
即
方程无解
…………………………………1分
iii) 若PB=PQ
由
得
…………………1分
整理得
解之得：
（舍去）………1分
综上可知， 当秒或
秒时，以B、P、Q三点为顶点的三角形是等腰三角形.
（3）如图2，
………1分
…………………1分
过Q作
于E，
…………………1分
（4）如图3，设存在时刻
，使得
，过点Q作
于G，
可证
…………………1分
∴
…………………1分
当
秒时，…………………1分