初三(上)第一学月考试数学试题
一、选择题：（14×3分=42分
1、Rt△ABC中,∠C=900，AC=5，BC=12，则其外接圆半径为（ ）
A、5 B、12 C、13 D、6.5
2、一元二次方程x2-3x-1=0与x2-x +3=0所有实数根 之和为（ ）
A、2 B、—4 C、4 D、3
3、在Rt△ABC中，∠C=900，a、b、c为三边，则下列等式中不正确的是( ）
A、a=csinA B、a=bcotB C、b=csinB D、c=
4、下列语句中，正确的有（ ）个
（1）三点确定一个圆.（2）平分弦的直径垂直于弦
（3）长度相等的弧是等弧.（4）相等的圆心角所对的弧相等
A、0个 B、1个 C、2个 D、3个
5、下列结论中正确的是（ ）
A、若α+β=900，则sinα= sinβ; B、sin（α+β）=sinα+sinβ
C、cot 470- cot 430 ＞0
D、Rt△ABC中 ，∠C=900，则sinA+cosA＞1，sin2A+sin2 B=1
6、过⊙O内一点M的最长弦为4cm，最短弦为2cm，则OM的长为（ ）
A、
B、
C、1 D、3
7、a、b、c是△ABC的三边长，则方程cx2+(a+b) x + 
=0 的根的情况是（ ）
A、没有实数根 B、有二个异号实根
C、有二个不相等的正实根 D、有二个不相等的负实根
8、已知⊙O的半径为6cm，一条弦AB=6cm，则弦AB所对的圆周角是（
）
A、300 B、600 C、600或1200 D、300 或1500
9、关于x的方程x2 - 2(1- k)x +k2 = 0有实数根α、β，则α+β的取值范围是（ ）
A、α+β≥1 B、α+β≤—1 C、α+β≥
D、α+β≤
10、设方程x2- x -1=0的二根为x1、x2 ，则x12、x22为二根的一元二次方程是（ ）
A、y2+3y+1=0 B、y2+3y-1=0 C、y2-3y-1=0 D、y2-3y +1=0
11、若x1≠x2，且x12-2x1-1=0，x22-2x2-1=0，则x1x2的值为（ ）
A、2 B、- 2 C、1 D、- 1
12、要使方程组
有一个实数解， 则m的值为（ ）
A、
B、±1 C、±
D、±3
13、已知cosα=
，则锐角α满足（ ）
A、00＜α＜300 ;B、300＜α＜450;C、450＜α＜600;D、600＜α＜900
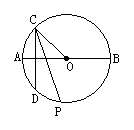
14、如图，C是上半圆上一动点，作CD⊥AB，CP平分∠OCD交⊙O于下半圆P，则当C点在上半圆（不包括A、B二点）移动时，点P将（ ）
A、随C点的移动而移动;B、位置不变;C、到CD的距离不变;D、等分
二、填空题（4×3分=12分）
1、某人上坡走了60米，实际升高30
米，则斜坡的坡度i=_______.
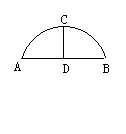
2、如图，一圆弧形桥拱，跨度AB=16m，拱高CD=4m，则桥拱的半径是______m.
3、在实数范围内分解因式：x2y-xy-y=____________________。
4、由一个二元一次方程和一个二元二次方程组成的方程组的解是
,
， 试写出一个符合以上要求的方程组：
_______________.
三、解答题（1 —4题，每题5分，5—6 题，每题6分，7—8题，每题7分，总分46分）
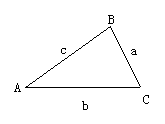
1、（5分）如图：在△ABC中，已知∠A=α，AC=b，AB=c.
(1)求证：S△ABC =
bcsinA. (2)若∠A=600，b=4，c=6，求S△ABC和BC的长。
2、（5分）用换元法解分式方程：
- 4x2 +7=0.
3.（5分）解方程组：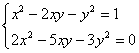
4、（5分）如图，AB=AC，AB是直径，求证：BC=2·DE.
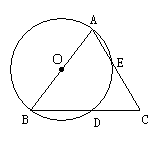
5、（7分）如图,DB=DC，DF⊥AC.求证：①DA平分∠EAC;②FC=AB+AF.
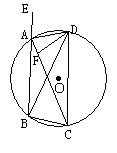
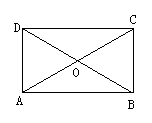
6、（7分）矩形的一边长为5，对角线AC、BD交于O，若AO 、BO的长是方程
x2+2（m-1）x+m2+11=0的二根，求矩形的面积。
7、（7分）已知关于x的方程x2-2mx+
n2=0，其中m、n是一个等腰△的腰和底边的长。
(1)求证：这个方程有二个不相等的实数根。
(2)若方程的二根x1、x2满足丨x1-x2丨=8，且等腰三角形的面积为4，求m、n的值。
8、（5分）如果一元二次方程ax2+bx+c=0的二根之比为2:3，试探索a、b、c之间的数量关系，并证明你的结论。
参考答案:
一. DDDAD,ADCAD,DBDB.
二.
1. 1：1;
2. 10;
3.
y(x-
)(x-
);
4.
.
三.
1.(1)作BD⊥AC于D,则
sinA=
,
∴ BD=c·sinA,
∵SΔABC=AC·BD
∴SΔABC =bcsinA.
(2) SΔABC=bcsinA
=×4×6×sin600
=6
.
2.原方程变为
设
=y,则原方程变为
-2y+1=0,即2y2-y-1=0.
∴ y=1 或y=-.
当y=1时,2x2-3=1,x=±2.
当y=-时,2x2-3=-,x=±
.
经检验,原方程的根是
±2, ±.
3.由(2)得 (2x+y)(x-3y)=0.
∴ y=2x 或x=3y.
∴原方程组化为
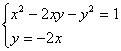或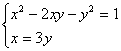
用代入法分别解这两个方程组,
得原方程组的解为
,
,
,
.
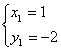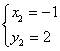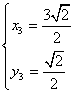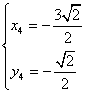4.连结AD.
∵AB是直径,
∴∠ADB=900.
∵AB=AC,
∴BD=DC, ∠BAD=∠CAD.
∴
,
∴BD=DE.
∴BD=DE=DC.
∴BC=2DE.
5.(1) ∵DB=DC,
∴∠DBC=∠DCB.
∵∠DBC=∠DAC, ∠DCB=∠DAE,
∴∠DAE=∠DAC,
∴AD平分∠EAC.
(2)作DG⊥AB于G.
∵DF⊥AC,AD=AD, ∠DAE=∠DAC,
∴ΔAFD≌ΔAGD,
∴AF=AG,DG=DF,
∵DB=DC,
∴ΔDBG≌ΔDCF,
∴GB=FC,
即FC=GA+AB,
∴FC=AF+AB.
6. ∵矩形ABCD中,AO=BO,
而AO和BO的长是方程的两个根,
∴Δ=(2m-2)2-4(m2+11)=0
解得m=-5.
∴x2-12x+36=0,
∴x1=x2=6,即AO=BO=6,
∴BD=2BO=12,
∴AB=
,
∴S矩形ABCD=5
.
7.
(1) ∵m和n是等腰三角形的腰和底边的长,
∴2m+n>0,2m-n>0,
∴Δ=4m2-n2=(2m+n)(2m-n)>0,
∴原方程有两个不同实根.
(2)∵丨x1-x2丨=8,
∴(x1-x2)2=64，
即(x1+x2)2-4x1x2=64,
∵x1+x2=2m,x1x2=n2,
∴4m2-n2=64. ①
∵底边上的高是
,
∴
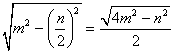. ②
① 代入②,得 n=2.
n=2代入 ①, 得 m=
.
8.结论:6b2=25ac.
证明:
设两根为2k和3k,则
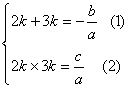
由(1)有 k=-
(3)
(3)代入(2)得 6×
,
化简,得 6b2=25ac.