![]() 信懋学校初三年级阶段性评估测试
信懋学校初三年级阶段性评估测试
| 题号 | 一 | 二 | 三 | 总分 |
| 应得分 | 30 | 24 | 46 | 100 |
|
|
一, 选择题(本题有10小题,每小题3分,共30分)
1.—3 的相反数是 ( )
(A)![]() (B)
3
(C)—
(B)
3
(C)— ![]() (D)—3
(D)—3
2. 地球上的海洋面积约为 千米2,用科学记数法表示为 ( )
![]() (A) 3.61×106 千米2
(B)3.61×107 千米2
(A) 3.61×106 千米2
(B)3.61×107 千米2
(C)3.61×108 千米2 (D)3.61×109 千米2
3.一组数据的每个数都减去5所得新数据的平均数为3,则原数据的平均数为 ( )
(A)2 (B) — 2 (C) 8 (D)15
![]() 4. 若圆锥的母线长为4cm,底面半径为3cm,则圆锥的侧面展开图的面积是( )
4. 若圆锥的母线长为4cm,底面半径为3cm,则圆锥的侧面展开图的面积是( )
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() ;
;
5.一个正方形的内切圆半径,外接圆半径与这个正方形边长的比为( )
(A)1∶2∶![]() ; (B)1∶
; (B)1∶![]() ∶2; (C)1∶
∶2; (C)1∶![]() ∶4; (D)
∶4; (D)![]() ∶2∶4;
∶2∶4;
![]() 6.若二次函数
6.若二次函数![]() 的图象如图所示,则点(a+b,ac)在(
)
的图象如图所示,则点(a+b,ac)在(
)
(A)第一象限; (B)第二象限;
(C)第三象限; (D)第四象限;
7.一个圆锥的底面半径为10,母线长30,则它的侧面展开图(扇形)的圆心角是( )
(A)60°
; (B)90°; (C)120°; (D)150°;
8.如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于( )
(A)20°; (B)30°; (C)40°; (D)50°;
 | |||||
 | |||||
 | |||||
(第6题) (第8题) (第9题)
9.如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连结BC,若△ABC面积为S,则( )
的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连结BC,若△ABC面积为S,则( )
(A)S=1; (B)S=2; (C)S=3; (D)S=![]() ;
;
10设x,y,z为实数,且x+y+z=5 ,xy+yz+zx=3 则z.的最小值为 ( )
(A)—1 (B)0 (C)1 (D)2
二. 填空题(每小题3分,共24分)
11. 两个不相等的无理数,它们的乘积为有理数,这两个数可以是______.
12.抛物线![]() 的对称轴是
;顶点的坐标是
;
的对称轴是
;顶点的坐标是
;
13.已知点P在第二象限,它的横坐标与纵坐标的和为1.点P的坐标是______(写出符合条件的一个点即可).
14如果两圆的半径分别为1和2,圆心距为![]() ,那么一条外公切线的长是
;
,那么一条外公切线的长是
;
15.若正多边形的一个内角等于140°,则它是正 边形;
16.观察图形的变化规律,写出第n个小房子用了
块石子
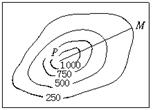
17.如图所示,测量队为了测量某地区山顶P的海拔高度.选择M点作为观测点.从M点测得山顶P的仰角为30°.在比例尺为1∶50000的该地区等高线地形图上,量得这两点间的图上距离为3厘米,则山顶P的海拔高度为______米(取![]() =1.732).
=1.732).
18.已知△ABC中,∠C=90°,AC=3,BC=4,分别以A,C为圆心作⊙A和⊙C与直线AB不相交,⊙A与⊙C相切,设⊙A的半径为r,则r的取值范围为
三.解答题(19,20题各4分;21,22题各5分;23题4分;24题10分;25题14分;共46分)
19.计算:(—2)0+ 4×(—3) +3cos600
20.解方程组;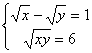
 21.如图已知,矩形ABCD中AC与BD相交一点,过C
,D分别作对角线的平行线相交于点。E求证:OE垂直平分CD
E
21.如图已知,矩形ABCD中AC与BD相交一点,过C
,D分别作对角线的平行线相交于点。E求证:OE垂直平分CD
E
D C
O
A B
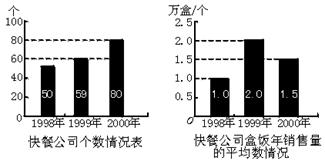
22.小李通过对某地区1998年至2000年快餐公司发展情况的调查,制成了该地区快餐公司个数情况的条形图(如图11)和快餐公司盒饭年销售量的平均数情况条形图(如图12).利用下面两副图共同提供的信息,解答下列问题:
(1)1999年该地区销售盒饭共______万盒.
(2)该地区盒饭销售量最大的年份是______年,这一年的年销售量是______万盒;
(3)这三年中该地区每年平均销售盒饭多少万盒?
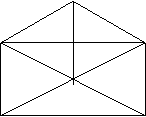
23.用四种方法把一个矩形分割成四个彼此相似而不全等的直角三角形.
![]()
![]()
24. 某汽车租赁公司共有30辆出租汽车,其中甲型汽车20辆,乙型汽车10辆。现将这30辆汽车租赁给A、B两地的旅游公司,其中20辆派往A地,10辆派往B地,两地旅游公司与汽车租赁公司商定每天价格如下表:
| 每辆甲型车租金(元/天) | 每辆乙型车租金(元/天) | |
| A地 | 1000 | 800 |
| B地 | 900 | 600 |
(1)设派往A地的乙型汽车![]() 辆,租赁公司这30辆汽车一天共获得的租金为
辆,租赁公司这30辆汽车一天共获得的租金为![]() (元),求
(元),求![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若要使租赁公司这30辆汽车一天所获得的租金总额不低于26800元,请你说明有多少种分派方案,并将各种方案设计出来;
(3)如果要使这30辆汽车每天获得的租金最多,请你为租赁公司提出合理的分派方案.
25.RT△ABC中直角边OA,OB分别在X轴,Y轴的正半轴上,O为坐标原点,以F为圆心的圆与Y轴,直线AB分别相切于O,D (如图)若AD=2,AE=1。
(1) 求BD的长度;
(2) 求经过A,B两点的直线解析式;
(3) 求经过E,D,O三点的二次函数的解析式;
(4) 判断(3)中的抛物线的顶点是否在直线AB上。
 Y
Y
B
D
|
O
(请仔细答题)