初三(上)数学试卷
一、填空题(共28分,每小题2分)
1、当a 时,关于x的方程(a-5)x2+bx-4=0是一元二次方程。
2、已知x1、x2是方程x2-3x+1=0的两个根,那么x1+x2= ,x1·x2= 。
3、圆的面积S(cm2)与它的半径R(cm)之间的函数关系式是S=πR2,其中变量是 ,常量是 。
4、圆的对称轴是 。
5、在Rt△ABC中,∠C=90°,BC=a,AB=c,AC=b,那么cosB= ,cotA= 。
 6、抛物线x2+2x-1=0的顶点坐标是
,对称轴是 。
6、抛物线x2+2x-1=0的顶点坐标是
,对称轴是 。
7、已知sin35°=0.5736,那么cos55°= 。
8、函数y=![]() 中,自变量x的取值范围是
。
中,自变量x的取值范围是
。
9、方程组的解是![]() 。
。
10、已知圆的直径为13cm,如果直线和圆心的距离为4.5cm,那么直线和圆 个公共点。
11、点P(-2,-3)关于原点对称的点的坐标是 。
12、在⊙O中弦AB的长为8cm,弦心距为3cm,那么⊙O的半径为 。
13、如果点P(1,2)在过原点的一条直线上,那么这条直线的解析式是 。
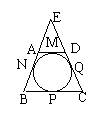
 14如图,⊙O与四边形ABCD的边分别相切于点M、N、P、Q,
14如图,⊙O与四边形ABCD的边分别相切于点M、N、P、Q,
BA、CD的延长线相交于点E,如果△BCE的周长为16,BC=4,
那么△ADE的周长为。
二、选购题(共14分,每小题2分)
1、如图,四边形ABCD为⊙O的内接四边形,那么( )
A、∠B=∠D B、∠B>∠D C、∠B+∠D=90° D、∠B+∠D=180°
2、下列方程中,有两个相等实数根的是( )
A、x2-4x+4=0 B、x2-2x+2=0 C、x2+x+1=0 D、x2+5x+3=0
3、下列式子正确的是( )
A、
 sin66°>sin68° B、tan66°>tan68°
sin66°>sin68° B、tan66°>tan68°
C、cos66°>cos68° D、cot66°<cot68°
4、如图,在⊙O中,∠AOB=92°,那么∠ACB的度数为( )
A、92° B、46° C、84° D、以上都不对。
5、△ABC的内切⊙O和各边分别相切于点D、E、F,那么O是△DEF的( )
A、三条中线的交点 B、三条高线的交点
C、三条角平分线的交点 D、三条边的中垂线的交点
6、函数y=(3m-1)x是正比例函数,且y随自就量x的增大而增大,那么m的取值范围是( )
A、m>1/3 B、m<1/3 C、m≥1/3 D、m≤1/3
7、在实数范围内把二次三项式x2+x-1=0分解因式正确的是( )
A、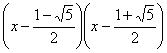 B、
B、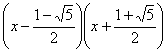
C、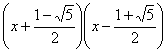 D、
D、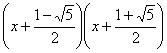
三、(共18分,每题6分)
1、
计算cos230°-![]() sin45°·tan45°+sin30°
sin45°·tan45°+sin30°
 2、如图,在离地面高度为5米处引拉线固定电线杆,拉线和地面成66°的角,求拉线AC的长及拉线下端点A与杆底D的距离;(精确到0.1米) 参考数据sin66°=0.9135,cos66°=0.4067,tan66°=2.246,cot66°=0.4452。
2、如图,在离地面高度为5米处引拉线固定电线杆,拉线和地面成66°的角,求拉线AC的长及拉线下端点A与杆底D的距离;(精确到0.1米) 参考数据sin66°=0.9135,cos66°=0.4067,tan66°=2.246,cot66°=0.4452。
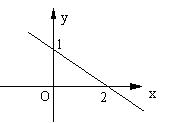 3、一次函数的图象如图所示,且点(m,3)在这个图象上,求这个一次函数的解析式和m的值。
3、一次函数的图象如图所示,且点(m,3)在这个图象上,求这个一次函数的解析式和m的值。
四(共18分,每小题6分)
1、用配方法解方程 x2-4x-3=0 2、用换元法解方程 ![]()
2、
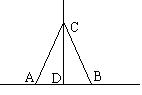
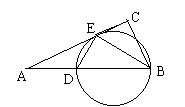 已知:如图在△ABC中,∠C=90°,BE是角平分线,DE⊥BE交AB于点D;
已知:如图在△ABC中,∠C=90°,BE是角平分线,DE⊥BE交AB于点D;
求证:AC是△BDE的外接圆的切线。
五、(共10分,每小题5分)
1、 列方程解应用题:从A站到B站共有120千米,一辆客车和一辆货车同时从A站出发,行驶了1小时的时候,客车在货车前面24千米,客车到达B站比货车早25分钟,求客车和货车每小时各走多少千米?
2、
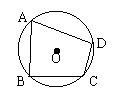
 已知:如图,△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,过D作
已知:如图,△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,过D作
DE⊥AC交于点E,求证:BD2=AC·EC。
六、(6分)
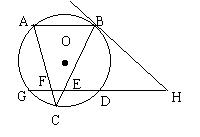
已知:如图,△ABC内接于⊙O,BH是⊙O的切线,⊙O的割线HDG分别交BC和AC于点E、F,且EG·ED=EH·EF,求证:AB∥GH。
七、(共6分)
一次函数y=kx+b的图象在第一、二、四象限内,且经过点(6,4)和(0,t),与x轴交于点P,与直线y=4x交于点Q。
(1)用含t的代数式表示Q的纵坐标和△POQ的面积(O为坐标原点);
(2)设△POQ的面积等于40,求函数y=kx+b的解析式。