北京市东城区2005年初三年级综合练习（一）
初三数学
第I卷 （选择题44分）
一、选择题：本题共11个小题，每小题4分，共44分，在每小题给出的四个选项中，只有一个是符合题目要求的。
1、下列各组数中，互为倒数的是
A、-2和2 B、 
和-2 C、2和 D、2和 
2、如图在Rt△ABC中，∠C=90°， 
，则cosB的值为
A、 
B、 
C、 
D、 
3、下列各式中，运算正确的是
A、m3+m2=m5
B、m3·m2=m6
C、(4m2)3=4m6
D、3m2÷m2=3
4、十届人大三次会议温总理在政府工作报告中指出，今年中央财政将安排万元解决下岗工人的再就业问题，这个数字用科学记数法表示成
A、109×104万元 B、1.09×104万元 C、1.09×105万元 D、1.09×106万元
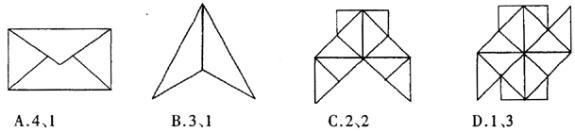
5、观察下列用纸折叠成的图案，其中轴对称图形和中心对称图形的个数分别是
6、函数 
中，自变量x的取值范围是
A、x≥0 B、x>0且x≠1 C、x>1 D、x≥0且x≠1
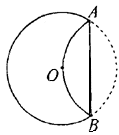7、如图，半径为4的⊙O中有弦AB，以AB为折痕对折，劣弧恰好经过圆心O，则弦AB的长度等于（ ）
A、 
B、4 C、 
D、
8、化简 
的结果是
A、1 B、x2+1 C、x2-1 D、
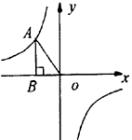9、如图，A为双曲线 
上的一点，直角三角形ABO的面积为2，则k的值为
A、4 B、-4 C、-2 D、-1
10、如果两圆的直径是方程x2-10x+24=0的两根，两圆圆心距为5，则这两个圆的公切线共有（ ）
A、1条 B、2条 C、3条 D、4条
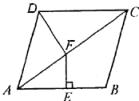
11、如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，E为垂足，连结DF，则∠CDF等于
A、60° B、65° C、70° D、80°
第II卷（填空题20分，解答题56分）
二、填空题：本大题共5小题，每小题4分，共20分，把答案填在题中的横线上。
12、阿拉木图与乌鲁木齐时差2个小时，飞机于18：20从乌鲁木齐起飞，到达阿拉木图时，当地时间为18：10，那么从乌鲁木齐到阿拉木图的飞行时间为_______分钟.
13、若a、b都是无理数，且ab=1，则a、b的值可以是_________________________（填上一组满足条件的值即可）.
14、某校对初三（1）班50名学生进行了“一周（按7天计算）做家务所用时间（单位：小时）”的调查如下表：
| 一周做家务所用时间（单位：小时） | 0.5 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 4 |
| 学生人数 | 8 | 12 | 9 | 7 | 6 | 5 | 2 | 1 |
则该校这50个学生一周做家务所用时间的众数为________(小时)，中位数为_______(小时).
15、已知圆锥的母线长是5cm，底面半径为3cm，那么它的侧面展开图的面积是______cm2。
16、一次函数y=ax+b的图象过点P(1，2)，且与x轴交于点A，与y轴交于点B，若 
，则点B的坐标是___________________。
三、解答题：本大题共9小题，共56分，解答应写出文字说明、证明过程或演算步骤。
17、（本题5分）因式分解：a3+ab2-2a2b-a.
18、（本题5分）计算：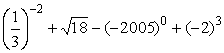 
.
19、（本题6分）解方程： 
.
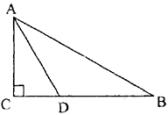
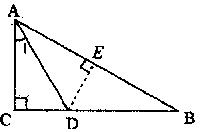
20、（本题5分）如图，在Rt△ABC中，∠C=90°，AC=6，∠A的平分线 
，求△ABD的面积。
21、（本题6分）为了节约能源，某小区物业在冬季供暖之前就制定了详细的燃煤计划，如果每天比计划多烧一吨，那么冬季用煤将超过2500吨；如果每天比计划节约一吨，那么冬季用煤将会不足2300吨，如果供暖时间按120天计算，那么应计划每天用煤控制在什么范围？（精确到0.1）
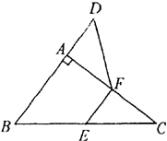
22、（本题6分）如图，在△ABC中，∠BAC=90°，延长BA到点D，使 
，点E、F分别为BC、AC的中点，请你在图中找出一组相等关系，使其满足上述所有条件，并加以证明。
23、（本题7分）已知关于x的一元二次方程(m+1)x2-2(m+1)x+m-1=0.
（1）当m取何值时，方程有两个实数根？
（2）设x1、x2是方程的两个实数根，且满足 
，求m的值.
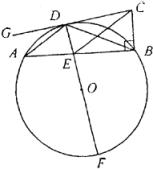
24、（本题8分）如图，⊙O的直径DF与弦AB交于点E，C为⊙O外一点，CB⊥AB于点B，G是直线CD上一点，∠ADG=∠ABD，AD//CE.
（1）求证：AD·CE=DE·DF.
（2）若∠DAE=30°，BC=2， 
，AE：BE=2：3，求 
的长。
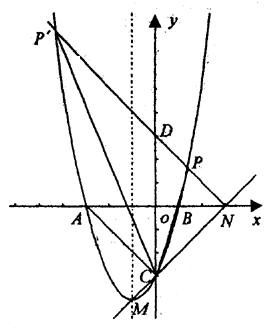
25、（本题8分）已知二次函数y=a(x+1)2+m的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于C，顶点为M，直线MC的解析式为y=kx-3，且直线MC与x轴交于点N， 
.
（1）求直线MC及二次函数的解析式；
（2）在二次函数的图象上是否存在点P（异于点C），使以点P、N、C为顶点的三角形是以NC为一条直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由。
北京东城区2005年初三年级综合练习(一)
初三数学参考答案
一、选择题(每小题4分，共44分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 | C | A | D | D | B | D | C | D | B | C | A |
二、填空题(每小题4分，共20分)
12. 110；13. 
14.
1, 1.2；15.15π.16. 
三、解答题(共56分)
17.(本题5分)
解：原式=a(a2+b2-2ab-1)……………………………………………………3分
=a[(a-b)2-1]…………………………………………………………4分
=a(a-b+1)(a-b-1)……………………………………………………5分
18.(本题5分)
解：原式 
………………………………………………………4分
…………………………………………………………………5分
19. (本题6分)
解：设x2+2x=y，则原方程化成 
………………………………………1分
化简，得y2-2y-8=0
解这个方程，得y1=4，y2=-2.……………………………………………………3分
当y=4时，x2+2x-4=0，解得 
；…………………………4分
当y=-2时，x2+2x+2=0，这时△=4-8<0，此方程无实数根.……………5分
经检验， 都是原方程的根.
∴原方程的根为 .………………………………………6分
20.(本题5分)
解：过点D作DE⊥AB于E.………………………………………1分
在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，
∴DE=CD
∵AC=6， 
，
.
∴∠1=30°…………………………………………………………………2分
…………………………………………………………………3分
这时∠BAC=60°，∠B=30°.
∴AB=2AC=12.………………………………………………………………4分
………………………………………5分
21.(本题6分)
解：设计划每天用煤x吨.……………………………………………………1分
依题意，得 
……………………………………………………3分
解这个不等式组，得 
即19.8<x<20.2.…………………………………………………………………5分
答：应计划每天用煤控制在19.8~20.2吨的范围.………………………………6分
22.(本题6分)
答：BE=DF.(或∠B=∠D，∠AFD=∠C等.如果所得结论只用了一个条件此题只给2分，用了两个条件，给4分，三个条件全用上了，给全分)……………1分
证法一：作EH⊥AB于H，如图.……………………………………………2分
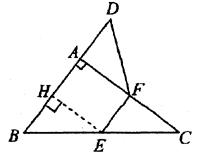在△ABC中，∠BAC=90°
∴EH∥AC，∠BHE=∠DAF=90°
∵E、F分别是BC、AC的中点，
∴H是AB的中点， 
………………………………………3分
∴BH=AD……………………………………………………………………4分
∴△BEH≌△DFA(SAS)……………………………………………………5分
∴BE=DF……………………………………………………………………6分
证法二：连结AE如图.……………………………………………………2分
在△ABC中，E、F分别是BC、AC的中点，点D在BA的延长线上，
.
∴EF=AD
∴四边形AEFD是平行四边形.………………………………………3分
∴AE=DF…………………………………………………………………4分
∵∠BAC=90°
…………………………………………………………5分
∴BE=DF…………………………………………………………………6分
23.(本题7分)
解：(1)依题意，有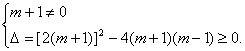 
………………2分
解得m>-1…………………………………………………………3分
(2)由根与系数的关系，得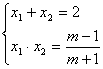 
…………………………4分
…………………………5分
整理，得m2+2m-3=0.
解得m1=1，m2=-3.……………………………………………………6分
由于m>-1，故m=-3不合题意，舍去.
所以m=1为所求。……………………………………………………7分
24.(本题8分)
(1)证明：连结AF……………………………………………………1分
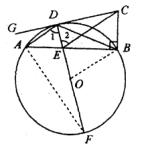∵DF是⊙O的直径，
∴∠DAF=90°
∵∠ADG=∠ABD
而∠F=∠ABD。
∴∠ADG=∠F
∵∠F+∠1=90°
∴∠ADG+∠1=90°
∴CG是⊙O的切线，∠CDE=90°………………………………………2分
∵AD∥CE，∴∠1=∠2，∴△ADF∽△DEC.……………………………3分
即AD·CE=DE·DF.……………………………………………………………4分
(2)解：∵AD∥CE，∠DAE=30°
∴∠CEB=∠DAE=30°
在Rt△EBC中，∵BC=2，
∴CE=4， 
∵AE：BE=2：3， 
…………………………………………5分
设DE=x,DF=y
∵AD·CE=DE·DF， 
，
∴xy=10……………………………………………………………………6分
由AE·BE=DE·EF，得 
解得x2=2. 
………………………………………7分
连结OB,于是∠DOB=60°
∴ 
………………………………………8分
25.(本题8分)
解：(1)二次函数y=a(x+1)2+m的图象的顶点M(-1,m)，
由直线MC的解析式y=kx-3,得C(0,-3)………………………………………1分
设OB=t， 
，则OC=3t.
∵OC=3，∴3t=3
∴t=1.∴OB=1…………………………2分
∵点B(1,0)，C(0,-3)都在二次函数的图象上，
∴二次函数的解析式为：y=x2+2x-3………………4分
∵点M(-1，-4)在直线MC上，
∴-4=-k-3即k=1.
∴直线MC的解析式为：y=x-3.………………………………………5分
(2)存在这样的点P.
①由于∠CNO=45°，则N(3,0)，在y轴上取点D(0,3)，连结ND交抛物线于点P(如图).
∴PNC=90°
直线ND的解析式为：y=-x+3.
解方程组 
得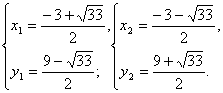 
………………………………………7分
②由于点A是二次函数图象与x轴的另一交点，故A(-3,0)。连结AC(如图)，∠ACN=90°，点A就是所求的点P(-3,0)
综上，满足条件的点为P1(-3，0)， 
……………………………………………………8分