初三数学阶段测试B卷
命题时间：10月10日
本卷总分为130分，时间为100分钟
一、填空题：（每题2分共30分）
1、方程
化为一元二次方程的一般形式为
。、
2、若
、
满足
，
，则
的值等于
。
3、方程
的解为
。
4、若一元二次方程
满足
，则该方程必有一根为 。
5、方程
的两根为
，则
=
。
6、若方程
的两根为
和4，则二次三项式
应该分解为 。
7、一件商品原价
元，连续两次均降价10%，则现价为
。
8、某钢铁厂去年第一季度增长率为20%，3月份钢产量7200吨，设1月份钢产量
吨，则可列方程为 。
9、当
时，方程
会产生增根。
10、方程组
的解为
。
11、在△ABC中，∠C=900，
，则
。
12、在Rt △ABC中，∠C=900，若
，则∠A= 。
13、一斜坡的坡度
，则坡角
= 。
14、计算：3cot600－
= 。
15、等腰三角形顶角为1200，底边上的高为4cm，则底边长为 。
二、选择题：（每题3分共30分）
16、 若sinA＜
，则锐角A一定……………………………………………（ ）
A、小于600 B、大于600 C、小于300 D、大于450
17、Rt△ABC中，若sinA=
,那么tanB的值（∠C=900）为 …………………（ ）
A、
B、
C、
D、
18、Rt△ABC中∠C=900，
，
，则斜边
的长为…（ ）
A、10 B、14 C、20 D、24
19、某人在距一建筑物100米处测得该建筑物顶部的仰角为600，则该建筑物的高度为（ ）
A、50米 B、100米 C、
米
D、100
米
20、等腰三角形一腰上的高为，这高与底的夹角是600，则
=………（ ）
A、
B、
C、
D、3
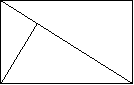
21、如图，矩形ABCD中，AB=3，BC=4，BE⊥AC，垂足为E，则sin∠ABE的值（ ）
A、
B、
C、
D、
A
D
E
B C
22、下列方程中，有实数根的方程是………………………………………………（ ）
A、
B、
C、
D、
23、某厂计划用天生产机床120台，由于采用新技术，每天多生产3台，则可提前2天完成，由题意可列方程…………………………………………………………………（ ）
A、
B、
C、
D、
24、若关于
的方程组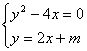
有两个不同的实数解，则
的取值范围是（ ）
A、≥
B、≤
C、＞
D、＜
25、若方程的方程
的两根互为相反数，则
的值为（ ）
A、0
B、4
C、0或4 D、0或
三、解答题：
26、若关于的方程
有一个正根和负根，且正根的绝对值较小，求整数的值。（本题6分）
27、已知：方程
，求作一个一元二次方程，使它的一根为原方程和的倒数，另一根为原方程两根差的平方。（本题6分）
28、在实数范围内分解因式：（本题8分）
（1）、
（2）、
四、应用题：
29、某车间加工300个零件，在加工完80个后，改进了操作方法，每天能多加工15个，一共用6天完成了任务，求改进操作方法后每天加工的零件数。（本题5分）
30、小明将勤工俭学挣得的100元钱，按一年定期存入银行，到期后取出50元，剩下的50元和应得的利息，又全部按一年定期存入，若存款的年利率保持不变，这样到期后可得本金和利息共66元，求这种存款的年利息。（本题6分）
五、解答题：
31、为何值时方程组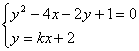
（1）有两个相等的实数根，并求出此时的解。
（2）无实数解。（本题6分）
32、在Rt△ABC中，∠C=900，斜边C=5，两直角边长分别为关于的方程
的根，求的值。（本题6分）
33、已知关于的方程
，
（1）、取什么实数时，方程有两个相等的实数根？
（2）、是否存在实数，使方程的两根满足
，若存在求出方程的两根，若不存在说明理由。（本题8分）
34、已知等腰梯形下底长为12，高为6，下底角的余弦值为，求梯形的上底长。（本题5分）
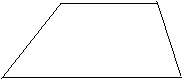
35、如图，水坝的横截面积为梯形，坝顶宽6米，坝高4米，坡AB的坡度为
，坡CD的坡角为600，求坝底宽BC（本题7分）
A
D
B E C
36、一艘船以每小时20海里的速度向正东方向航行，上午8时位于A处，这时灯塔S在船的北偏东450方向上，上午9时30分船B处，这时灯塔S在此船的北偏东300方向上，若船继续航行，求船和灯塔之间的最短距离。（本题7分）
北
S
东
