初三上学期复习讲义一元二次方程
一.
知识归纳
1 一元二次方程概念ax2+bx+c=0(a≠0)
2 解法①直接开平方法②配方法③公式法④因式分解法
3 根的判别式⊿△=b![]() -4ac
-4ac
4 根与系数关系![]() +
+ ![]() =
=![]() ,
, ![]() ·
·![]() =
=![]()
二.
填空题
1方程![]() 的解为__________,方程
的解为__________,方程![]() 的解为________若关于x的二次方程(m+1)x2-3x+2=0有两个相等的实数根,则m=______.
的解为________若关于x的二次方程(m+1)x2-3x+2=0有两个相等的实数根,则m=______.
2设方程![]() 的两根分别为
的两根分别为![]() ,
,![]() ,则
,则![]() +
+ ![]() =______,
=______,![]() ·
·![]() =________
=________
![]() ________,
________, ![]() =________,
=________, ![]() =___________
=___________
3 若方程x2-5x+m=0的一个根是1,则m=________
4 两根之和等于-3,两根之积等于-7的最简系数的一元二次方程是________
5 已知方程2x2+(k-1)x-6=0的一个根为2,则k=_______
6若关于x的一元二次方程mx2+3x-4=0有实数根,则m的值为______
7方程 ![]() 无实根,则
无实根,则
![]() ______
______
8如果 ![]() 是一个完全平方公式,则
是一个完全平方公式,则
![]() ______。
______。
9若方程 ![]() 的两根之差的绝对值是8,则
的两根之差的绝对值是8,则 ![]() ______。
______。
10若方程 ![]() 的两根之比为3,则
的两根之比为3,则 ![]() _____。
_____。
11在实数范围内分解因式:![]() ___________,
___________,![]() =____________
=____________![]() =______________
=______________![]() =____________
=____________
12若a,b为实数,且![]() ,则以a,b为根的一元二次方程是_______________
,则以a,b为根的一元二次方程是_______________
13以方程![]() 的两根的相反数为根的一元二次方程是______________
的两根的相反数为根的一元二次方程是______________
三. 选择题
1下列方程(1)-x2+2=0 (2)2x2-3x=0 (3)-3x2=0 (3)x2+![]() =0
=0
(5)![]() =5x (6)2x2-3=(x-3)(x2+1)中是一元二次方程的有( )
=5x (6)2x2-3=(x-3)(x2+1)中是一元二次方程的有( )
A、2个 B、3个 C、4个 D、5个
2下列配方正确的是( )
(1) x2+3x=(x+![]() )
)![]() -
-![]() (2)x2+2x+5=(x+1)2+4
(2)x2+2x+5=(x+1)2+4
(3)x2-![]() x+
x+![]() =(x-
=(x-![]() )2+
)2+![]() (4)3x2+6x+1=3(x+1)2-2
(4)3x2+6x+1=3(x+1)2-2
3方程(x-1)2+(2x+1)2=9x的一次项系数是( )
A、2 B、5 C、-7 D、7
4方程x2-3x+2-m=0有实根,则m的取值范围是( )
A、m>-![]() B、m≥
B、m≥![]() C、m≥-
C、m≥-![]() D、m>
D、m>![]()
5方程(m+1)x2-(2m+2)x+3m-1=0有一个根为0,则m的值为( )
A、![]() B、
B、![]() C、-
C、-![]() D、-
D、-![]()
6方程![]() 化为
化为![]() 形式后,a、b、c的值为( )
形式后,a、b、c的值为( )
(A)1,–2,-15 (B)1,-2,15(C)-1,2,15
(D)–1,2,–15
7方程![]() 的解的个数是( )
的解的个数是( )
(A)1 (B)2 (C)3 (D)4
8若方程![]() 的两根为x1,x2,下列表示根与系数关系的等式中,正确的是( )
的两根为x1,x2,下列表示根与系数关系的等式中,正确的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
9以![]() 和
和![]() 为根的一元二次方程是( )
为根的一元二次方程是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10如果一元二次方程![]() 的两个根是x1,x2,那么二次三项式
的两个根是x1,x2,那么二次三项式![]()
分解因式的结果是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11在实数范围内,![]() 可以分解为( )
可以分解为( )
(A)![]() (B)
(B)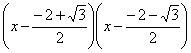
(C)![]() (D)
(D)![]()
12已知方程![]() 的两个根是互为相反数,则m的值是( )
的两个根是互为相反数,则m的值是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
13如果关于x的方程3ax2-2![]() (a-1)x+a=0有实数根,则a的取值范围是( )
(a-1)x+a=0有实数根,则a的取值范围是( )
A、a<![]() 且a≠0 B、a≥
且a≠0 B、a≥![]() C、a≤
C、a≤![]() 且a≠0 D、a≤
且a≠0 D、a≤![]()
14若方程2x(kx-4)-x2+6=0没有实数根,则k的最小整数值是( )
A、1 B、2 C、3 D、4
15一元二次方程一根比另一根大8,且两根之和为6,那么这个方程是( )
A、x2-6x-7=0 B、x2-6x+7=0 C、x2+6x-7=0 D、x2+6x+7=0
16已知方程![]() 的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角 形的斜边的长是( )
的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角 形的斜边的长是( )
(A)9 (B)6 (C)3 (D)![]()
17若一元二次方程![]() 的两根之比为3∶2,则
的两根之比为3∶2,则![]() 满足的关系式是( )
满足的关系式是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D) ![]()
18方程x2-2x-m=0有两个正实根,则m的取值范围是 ( )
A、0<m<1 B、m>0
C、-1≤m<0 D、m<-1
19一元二次方程ax2+bx+c=0(a≠0)的两根之和为m,两根平方和为n,则![]() 的值为(
)
的值为(
)
A、0 B、![]() C、
C、![]() D、
D、![]()
20已知关于![]() 的一元二次方程
的一元二次方程![]() 的两根
的两根![]() 满足
满足![]() ,则m的值为( )
,则m的值为( )
A、4 B、-36 C、4或-36 D、-36或-4
21若一元二次方程的两根![]() 满足下列关系:
满足下列关系:![]() 0,
0,
![]() ,则这个一元二次方程( )
,则这个一元二次方程( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
四. 解方程
1、![]() 2、
2、![]() 3、
3、![]()
4、![]() 5、
5、![]() 6、
6、![]()
五. 在实数范围内分解因式
1、![]() 2、
2、![]() 3、
3、![]()
六. 解答题
1已知方程![]() 的两个根是
的两个根是![]() ,求代数式
,求代数式
(1)![]() ;(2)
;(2)![]() 的值。
的值。
2、已知![]() 是一元二次方程
是一元二次方程![]() 的两根,求以
的两根,求以![]() 为根的
为根的
方程。
3、已知一元二次方程![]() ,求当k为何值时,方程有两个
,求当k为何值时,方程有两个
不相等的实数根?
4、求证:方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
5.已知关于x的方程![]()
1)若1是方程的一个根,求![]() 的值
的值
2)若方程有两个不相等的实数根,求![]() 的取值范围
的取值范围
6. 关于x的方程![]() 的两根之和为-1,两根之差为1
的两根之和为-1,两根之差为1
1) 这个方程的两个根
2) 求![]() :
:![]() :
:![]()
7. 证明:方程![]() 没有实数根
没有实数根
8. 已知αβ是方程![]() x2+(m-1)x+3=0的两根,且(α-β)2=16,m<0.求证:m=-1
x2+(m-1)x+3=0的两根,且(α-β)2=16,m<0.求证:m=-1
9. 已知αβ是方程ax2+bx-2=0的两根,
求证:以![]() 和
和![]() 为两根的方程是x2-bx –2a=0
为两根的方程是x2-bx –2a=0
10. 已知αβ是方程x2+4(m-1)x+12=0的两根,且![]() =4,m>0.求证:m=3
=4,m>0.求证:m=3
11. 已知x1,x2是关于x的方程x2-(2m+3)x+m2=0的两个实数根,
求证:![]() =1时m=3
=1时m=3
12. 已知一元二次方程8x2-(m-1)x+m-7=0,
⑴m为何实数时,方程的两个根互为相反数?
⑵ m为何实数时,方程的一个根为零?
⑶ 是否存在实数m,使方程的两个根互为倒数?
14已知:关于x的方程![]() x2-(m-2)x+m2=0,⑴若方程有两个相等的实数根,求m的值,并求出这时方程的根。 ⑵ 是否存在正数m,使方程的两个实数根的平方和等于224?若存在,请求出满足条件的m的值;若不存在,请说明理由。
x2-(m-2)x+m2=0,⑴若方程有两个相等的实数根,求m的值,并求出这时方程的根。 ⑵ 是否存在正数m,使方程的两个实数根的平方和等于224?若存在,请求出满足条件的m的值;若不存在,请说明理由。
15. m取何值时,方程![]()
(1)有两个不相等的实数根
(2)有两个相等的实数根;
(3)没有实数根