初三数学总复习测试十八模拟试卷五

初三数学总复习测试十八模拟试卷五

班级　　　　　 姓名　　　　 学号　　　　　 得分　　　　 

卷　　　 一

一、选择题

1、已知∣a∣=2，则a的值为（　　　 ）（2001山东临沂）

A　　2　　B　 ―2　  C　　±2　　D　　

2、下列说法中正确的是（　　　 ）（2001江苏扬州）

A　 ―1的绝对值是±1　　  B　 0的平方根是0

C　 是最简二次根式　　 D　 ()^―3等于

3、下列图形是中心对称图形的是（　　  ）（2001湖南常德）

A　　等腰梯形　 B　　等边三角形　 C　　正五边形　　D　　圆

4、用下面的语句至：① 所以∠A+∠B+∠C=90°+90°+∠C>180°，这与三角形内角和定理矛盾 ② 假设∠A、∠B、∠C中有两个直角，不妨令∠A=∠B=90° ③ 所以一个三角形中不能有两个直角　 组成用反证法证明“一个三角形中不能有两个角是直角”这一命题正确的证明过程，其排列次序依次是（　　　 ）（2001湖南常德）

A　　①②③　 B　　③②①　 C　 ②①③　 D　 ②③①

5、初三（1）班几个同学，毕业前合影留念，每人交0.70元，一张彩色底片0.68元，扩印一张相片0.50元，每人分一张，将收来的钱尽量用掉的前提下，这张相片上的同学最少有（　　　 ）（2001福建三明）

A　 2个　 B　 3个　　C　　4个　　D　　5个

6、如图，⊙A、⊙B、⊙C两两不相交，且半径都是0.5cm，则图中

的三个扇形（即三个阴影部分）的面积之和为（　　　 ）

（2001江西）

A　 cm²　 B　 cm²　 C　 cm²　 D　cm²

7、如果数据1，2，3，x的平均数是4，那么x等于（　　　　）（2001陕西）

A　　10　　B　　9　　C　　8　　D　　7

8、已知等腰三角形的一边等于3，一边等于6，则它的周长等于（　　　　）（2001陕西）

A　　12　　B　　12或15　　C　　15　　 D　　15 或18

9、解方程6(x²+)+5(x+)=38，若设x+=y，则原方程变为（　　　　）（2001山东烟台）

A　 6y²+5y―26=0　 B　 6y²+5y―38=0　 C　 6y²+5y―40=0　 D　 6y²+5y―50=0

10、一项工程，甲独立完成需要10天，乙独立需要15天，现在两人合作，完工后厂家共付给450元。如果按完成工程量的多少进行分配，则甲、乙各分得（　　　　）（2001山东烟台）

A　　 250元，200元　　 B　　260元，190元　

C　　 265元，185元　　 D　　270元，180元

11、已知点A和点B，以点A和点B为其中两个顶点作位置不同的

等腰直角三角形，一共可作出（　　　　）（2001广州）

A　 2个　 B　　4个　　C　　6个　　D　　8个

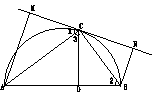12、如图，AB是圆O的直径，直线MN切半圆于C，CD⊥AB，

AM⊥MN，BN⊥MN，则下列结论中错误的是（　　　　）

（2001湖北天门）

A　　∠1=∠2=∠3　　　　　　  B　 CM=CD=CN

C　 △ACM∽△ABC∽△CBN　 D　 AM·CN=CM·BN

二、填空题

13、当x<1时，化简的结果为　　　　  （2001厦门）

14、分式有意义时，x的取值范围是　　　　　  。（2001青海）

15、方程组的解是　　　　　  。（2001山东烟台）

16、一个扇形的半径为6，圆心角为120°，用它做成一个圆锥

的侧面，则这个圆锥的底面半径为　　　　（2001山东威海）

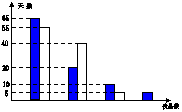
17、某厂对甲、乙两位优秀工人进行了为期100天的技术考核，

从而升任技术最好者为工长，考核结果如图，问应

确定　　　　 为工长？　　　　　　　　　　　　　　　  0　　　1　　 2　　3

18、研究下列算式你会发现有什么规律：

4×1×2+1=3²　 4×2×3+1=5²　　4×3×4+1=7²　　　4×4×5+1=9²　  ……

请你将找出的规律用含一个字母的等式表示出来：

　　　　　　　　　　　　　　　　　　　　　  （2001湖南常德）

三、解答题

19、tg60°+∣1―()^―1∣+2(―1)⁰―（2001湖北十堰）

20、化简：（2001江苏苏州）

21、△ABC中，AC⊥BC，CD⊥AB，垂足为D，∠A=30°，AC=6，求BC和BD（2001徐州）

22、已知：BC为半圆O的直径，AB=AF，AC和BF交于点M

（1）若∠FBC=α，求∠ACB（用α表示）

（2）过A作AD⊥BC于D，交BF于E，求证：BE=EM（2001江苏盐城）

23、某商场计划拨款9万元从厂家购进50台电视机。已知该厂家生产三种不同型号的电视机，出厂价分别为：甲种每台1500元，乙种每台2100元，丙种每台2500元。

（1）若商场同时购进其中两种不同型号电视机共50台，用去9万元，请你研究一下商场的进货方案

（2）若商场销售一台甲种电视机可获利150元，销售一台乙种电视机可获利200元，销售一台丙种电视机可获利250元。在同时购进两种不同型号电视机的方案中，为使销售时获利最多，你选择哪种进货方案？

（3）若商场准备用9万元同时购进三种不同型号的电视机50台，请你设计进货方案。（2001黑龙江）

24、已知抛物线y=―x²+2mx―m²―m+3与y轴的交点在原点的上方，

（1）试证明：该抛物线的顶点一定在直线y=―x+3上

（2）设该抛物线与x轴交于M、N两点，当OM·ON=3且OM≠ON时，求出这条抛物线的解析式（2001湖北随州）

25、如图，已知△ABC中，AB=AC，AF为△ABC的高，在△ABC的外接圆的AC上任取一点P，连结AP，交BC的延长线于E

（1）求证：△ABP∽△AEB

（2）设AP=x，AE=y，AB=a，求y与x之间的函数关系式，并确定x的取值范围

（3）当BC=8，a=4时，PAF的面积是否存在最大值？若存在，这时x的值是多少？若不存在，请说明理由。（2001湖南常德）