北京市东城区初中毕业统一考试
数学试卷
一、选择题（本题15小题，第1—8小题每小题3分，第9—15题每小题4分，共52分）在每个小题给出的四个选项中，只有一个是符合题目要求的，请把所选答案前的字母填在题后的括号里．
1．点P（-1，2）关于y轴对称的点的坐标是（ ）．
A．（1，2） B．（-1，2） C．（1，-2） D．（-1，-2）
2．抛物线
的顶点坐标是（ ）．
A．（2，1） B．（-2，1） C．（2，-1） D．（-2，-1）
3．关于x的方程
是一元二次方程，则（ ）．
A．a＞0 B．a≠0 C．a＝1 D．a≥0
4．如图，A、B、C三点在⊙O上，若∠AOB＝80°，则∠ACB等于（ ）．
A．160° B．80° C．40° D．20°
5．方程（x＋1）（x－2）＝0的根是（ ）．
A．x＝－1 B．x＝2
C．
D．
6．如果一组数据3，x，2，4的平均数是3，那么x是（ ）．
A．2 B．3 C．4 D．0
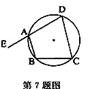7．如图，四边形ABCD为圆内接四边形，E为DA延长线上一点，若∠C＝50°，则∠BAE为（ ）．
A．130° B．100° C．50° D．45°
8．在ΔABC中，∠C＝90°，
，则cosA的值是（ ）．
A．
B．
C．
D．
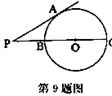
9．如图，PA切⊙O于点A，PBC是经过点O的割线，若∠P＝30°，则
的度数为（ ）．
A．30° B．60° C．90° D．120°
10．如果反比例函数
在其象限内，y随x的增大而减小，那么它的图象分布在( )
A．第一、二象限 B．第一、三象限
C．第二、三象限 D．第二、四象限
11．函数
的自变量x的取值范围是（ ）．
A．x＞2
B．x≤2 C．x＜2 D．x＜2且x≠0
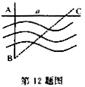
12．如图，为了测量河两岸A、B两点的距离，在与AB垂直的方向上取点C，测得AC＝a，∠ACB＝a，那么AB等于（ ）．
A．a·sinα B．a·cosα C．a·tanα D．a·cotα
13．方程组
的解是（ ）．
A．
B．
C．
D．
14．某型号的手机连续两次降价，每个售价由原来的1185元降到了580元．设平均每次降价的百分率为x，则列出方程正确的是（ ）．
A．
B．
C．
D．
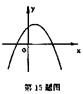
15．已知二次函数
的图象如图所示，则下列结论正确的是（ ）．
A．ab＞0，c＞0 B．ab＞0，c＜0 C．ab＜0，c＞0 D．ab＜0，c＜0
二、填空题（本小题共4小题，每小题4分，共16分）
16．已知A是锐角，且
，则cos（90°－A）＝___________．
17．直线
不经过第_______象限．
18．已知2是方程
的一个根，则2a－1＝__________．
19．如果两圆相切，那么它们的公切线有_________条．
三、解答题（本题共5小题，共32分）
20．（本题4分）计算：
．
21．（本题5分）解方程：
．
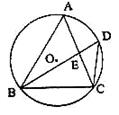22．（本题6分）如图，已知ΔABC内接于⊙O，D是⊙O上一点，连结BD、CD，AC、BD交于点E．
（1）请找出图中的相似三角形，并加以证明；
（2）若∠D＝45°，BC＝2，求⊙O的面积．
23．（本题8分）如果关于x的方程
没有实数根，试判断关于x的方程
的根的情况．
24．（本题9分）如图，直线
分别与x轴、y轴交于点A、B，⊙E经过原点O及A、B两点．
（1）C是⊙E上一点，连结BC交OA于点D，若∠COD＝∠CBO，求点A、B、C的坐标；
（2）求经过O、C、A三点的抛物线的解析式：
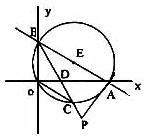（3）若延长BC到P，使DP＝2，连结AP，试判断直线PA与⊙E的位置关系，并说明理由．